Was sind das Erfassungsframework und die gängigen Algorithmen der Java-Datenstruktur?

1 Collection Framework

1.1 Collection Framework-Konzept

Java Collection Framework Das Java Collection Framework, auch Container-Container genannt, ist eine Reihe von Schnittstellen und deren Implementierungsklassen, die im Paket java.util definiert sind.

Seine Hauptleistung besteht darin, mehrere Elemente in einer Einheit zu platzieren, die zum schnellen und bequemen Speichern, Abrufen und Verwalten dieser Elemente verwendet wird, was allgemein als CRUD bekannt ist.

Übersicht über Klassen und Schnittstellen:

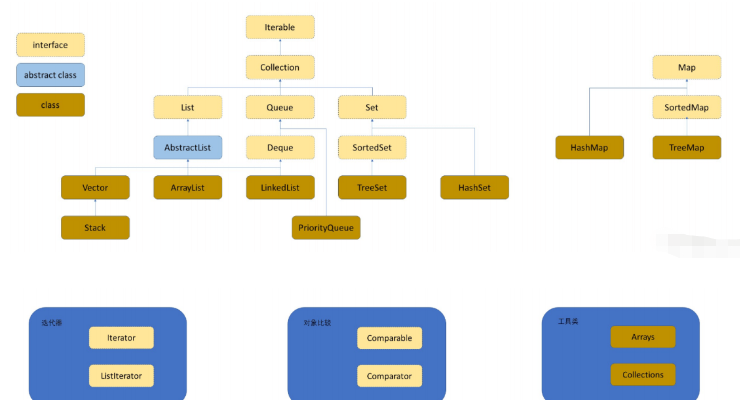
1.2 An Containern beteiligte Datenstrukturen

Collection: ist eine Schnittstelle, die einige Methoden enthält, die häufig in den meisten Containern verwendet werden.

List: ist eine Schnittstelle, die die Anforderungen in ArrayList und LinkedList standardisiert Implementierungsmethode

• ArrayList: implementiert die List-Schnittstelle, die unterste Ebene ist eine dynamische Typsequenztabelle

• LinkedList: implementiert die List-Schnittstelle, die unterste Ebene ist eine doppelt verknüpfte Liste

Stack: die unterste Ebene ist ein Stapel, und der Stapel ist eine spezielle Sequenztabelle

Queue: Die unterste Ebene ist eine Warteschlange, und die Warteschlange ist eine spezielle Sequenztabelle

Deque: Es ist eine Schnittstelle

Set: Es ist eine Menge, es ist eine Schnittstelle, in der das K-Modell platziert ist

• HashSet: Die unterste Ebene ist ein Hash-Bucket, die zeitliche Komplexität der Abfrage beträgt O(1)

• TreeSet: Die untere Ebene ist rot-schwarz Baum, die zeitliche Komplexität der Abfrage beträgt O(), ungefähr nach Schlüssel geordnet

Map: Mapping, innen Was gespeichert wird, ist das Schlüssel-Wert-Paar des K-V-Modells

• HashMap: Die unterste Ebene ist ein Hash-Bucket, und die Komplexität der Abfragezeit beträgt O(1)

• TreeMap: Die unterste Ebene ist ein rot-schwarzer Baum, und die Komplexität der Abfragezeit beträgt O( ), ungefähr Schlüsselreihenfolge

2 Algorithmus

2.1 Algorithmuskonzept

Algorithmus (Algorithmus): Es handelt sich um einen genau definierten Berechnungsprozess, der einen oder eine Gruppe von Werten als Eingabe verwendet. Ein Algorithmus ist eine Reihe von Rechenschritten, die dazu dienen, Eingabedaten in Ausgabeergebnisse umzuwandeln.

2.2 Algorithmuseffizienz

Die Algorithmuseffizienzanalyse ist in zwei Typen unterteilt: Der erste ist die Zeiteffizienz und der zweite ist die Raumeffizienz. Zeiteffizienz wird als Zeitkomplexität bezeichnet, während Raumeffizienz als Raumkomplexität bezeichnet wird. Die Zeitkomplexität misst hauptsächlich die Laufgeschwindigkeit eines Algorithmus, während die Raumkomplexität hauptsächlich den zusätzlichen Speicherplatz misst, den ein Algorithmus benötigt. In den Anfängen der Computerentwicklung war die Speicherkapazität von Computern sehr gering. Daher liegt uns die Komplexität des Weltraums sehr am Herzen. Mit der rasanten Entwicklung der Computerindustrie hat die Speicherkapazität von Computern ein sehr hohes Niveau erreicht. Daher müssen wir der räumlichen Komplexität eines Algorithmus keine besondere Aufmerksamkeit mehr schenken.

3 Zeitkomplexität

3.1 Konzept der Zeitkomplexität

Zeitkomplexität ist eine mathematische Funktion in der Informatik, die die Laufzeit eines Algorithmus darstellt und die Zeiteffizienz des Algorithmus quantitativ beschreibt. Die Ausführungszeit eines Algorithmus kann nicht theoretisch berechnet werden. Der Zeitaufwand kann erst ermittelt werden, nachdem das Programm tatsächlich auf dem Computer ausgeführt wurde. Obwohl jeder Algorithmus auf einem Computer getestet werden kann, ist dies sehr umständlich, sodass es eine Möglichkeit gibt, ihn anhand der Zeitkomplexität zu analysieren. Die zeitliche Komplexität eines Algorithmus ist proportional zur Zeit, die zum Ausführen der Anweisungen benötigt wird, und die zeitliche Komplexität hängt von der Anzahl der Ausführungen der Grundoperationen im Algorithmus ab.

3.2 Asymptotische Notation von Big O

// 请计算一下func1基本操作执行了多少次？
void func1(int N){
	int count = 0;
	for (int i = 0; i < N ; i++) {
		for (int j = 0; j < N ; j++) {
			count++;
		}
	}
	for (int k = 0; k < 2 * N ; k++) {
		count++;
	} 
	int M = 10;
	while ((M--) > 0) {
		count++;
	} 
	System.out.println(count);
}

Anzahl der von Func1 durchgeführten Grundoperationen: F(N)=N^2+2*N+10

• N = 10 F(N) = 130

• N = 100 F(N) = 10210

• N = 1000 F(N) = 1002010

Tatsächlich müssen wir bei der Berechnung der zeitlichen Komplexität nicht unbedingt die genaue Anzahl der Ausführungen berechnen. aber nur brauchen Ungefähre Anzahl der Ausführungen, daher verwenden wir hier die asymptotische Darstellung von Big O.

Big-O-Notation: Dabei handelt es sich um eine mathematische Notation zur Beschreibung des asymptotischen Verhaltens einer Funktion.

3.3 Ableitung der Big-O-Order-Methode

• Ersetzen Sie alle additiven Konstanten zur Laufzeit durch die Konstante 1.

• In der modifizierten Laufzeitfunktion wird nur der Term höchster Ordnung beibehalten.

• Wenn der Term höchster Ordnung existiert und nicht 1 ist, entfernen Sie die Konstante multipliziert mit diesem Term. Das Ergebnis ist die Big-O-Ordnung.

Nach Verwendung der asymptotischen Darstellung von Big O beträgt die zeitliche Komplexität von Func1: O(n^2)

• N = 10 F(N) = 100

• N = 100 F(N) = 10000 . Darüber hinaus gibt es beste, durchschnittliche und schlechteste Fälle für die zeitliche Komplexität einiger Algorithmen:

Schlimmster Fall: die maximale Anzahl von Läufen (Obergrenze) für jede Eingabegröße

• Durchschnittlicher Fall: die erwartete Anzahl von Läufen für jede Eingabe Größe

beste Situation: Mindestanzahl von Läufen (Untergrenze) für jede Eingabegröße

Zum Beispiel: Suche nach Daten

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

4 空间复杂度

对于一个算法而言，空间复杂度表示它在执行期间所需的临时存储空间大小。空间复杂度的计算方式并非程序所占用的字节数量，因为这并没有太大的意义；实际上，空间复杂度的计算基于变量的数量。大O渐进表示法通常用来计算空间复杂度，其计算规则类似于实践复杂度的计算规则。

实例1:

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {
	for (int end = array.length; end > 0; end--) {
		boolean sorted = true;
		for (int i = 1; i < end; i++) {
			if (array[i - 1] > array[i]) {
				Swap(array, i - 1, i);
				sorted = false;
			}
		} 
		if(sorted == true) {
		break;
		}
	}
}

实例2:

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {
	long[] fibArray = new long[n + 1];
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; i++) {
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
	} 
	return fibArray;
}

实例3:

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
	return N < 2 ? N : factorial(N-1)*N;
}

• 实例1使用了常数个额外空间，所以空间复杂度为 O(1)

• 实例2动态开辟了N个空间，空间复杂度为 O(N)

• 实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

Das obige ist der detaillierte Inhalt vonWas sind das Erfassungsframework und die gängigen Algorithmen der Java-Datenstruktur?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!