Heim >Backend-Entwicklung >Python-Tutorial >So implementieren Sie den Merge-Sortieralgorithmus in Python
So implementieren Sie den Merge-Sortieralgorithmus in Python
- PHPznach vorne
- 2023-05-21 08:31:361340Durchsuche
Algorithmusbeschreibung
Der erste erweiterte Sortieralgorithmus in diesem Abschnitt ist die Zusammenführungssortierung. Das Wort „Merger“ bedeutet „verschmelzen“. Wie der Name schon sagt, handelt es sich beim Zusammenführungssortierungsalgorithmus um einen Algorithmus, der die Sequenz zunächst in Untersequenzen aufteilt, die Untersequenzen sortiert und dann die geordneten Untersequenzen zu einer vollständigen geordneten Sequenz zusammenführt. Es übernahm tatsächlich die Idee des Teilens und Herrschens.
Die durchschnittliche Zeitkomplexität der Zusammenführungssortierung beträgt O(nlgn), die Zeitkomplexität beträgt im besten Fall O(nlgn) und die Zeitkomplexität im schlechtesten Fall beträgt ebenfalls O(nlgn). Seine räumliche Komplexität beträgt O(1). Darüber hinaus ist Merge Sort ein stabiler Sortieralgorithmus.
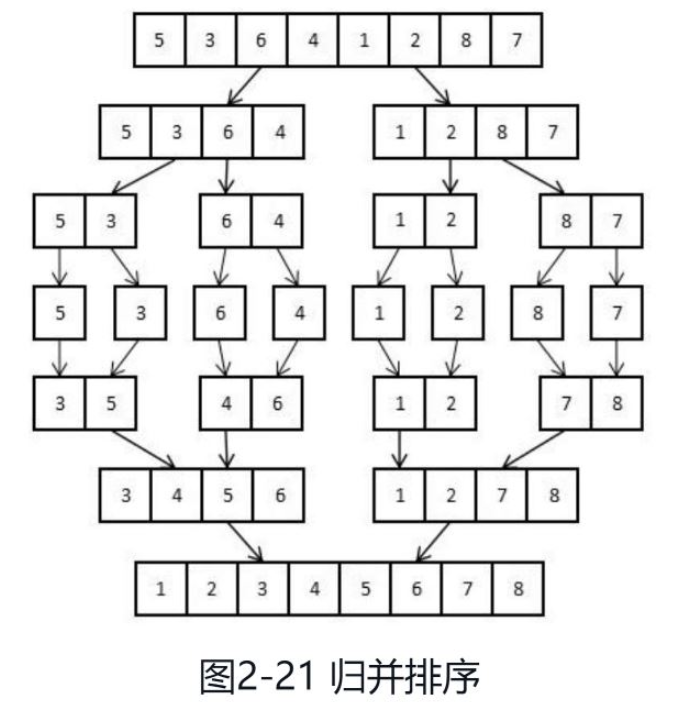
Am Beispiel der aufsteigenden Sortierung ist der Ablauf des Zusammenführungsalgorithmus in Abbildung 2-21 dargestellt.
Das ursprüngliche Array ist ein ungeordnetes Array mit 8 Zahlen. Nach einer Operation wird das Array mit 8 Zahlen in zwei ungeordnete Arrays mit 4 Zahlen aufgeteilt. Jede Operation teilt das ungeordnete Array in zwei Hälften, bis alle kleinsten Unterarrays nur noch ein Element enthalten. Wenn das Array nur ein Element enthält, muss das Array geordnet sein. Dann beginnt das Programm, alle zwei kleinen geordneten Arrays zu einem großen geordneten Array zusammenzuführen. Zuerst werden zwei Arrays mit einer Zahl zu einem Array mit zwei Zahlen zusammengeführt, dann werden zwei Arrays mit zwei Zahlen zu einem Array mit vier Zahlen zusammengeführt und schließlich werden zwei Arrays mit zwei Zahlen zu einem Array mit acht Zahlen zusammengeführt. Wenn alle geordneten Arrays kombiniert werden, wird das am längsten gebildete geordnete Array sortiert.
Code-Implementierung
Sortiercode zusammenführen:
#归并排序
nums = [5,3,6,4,1,2,8,7]
def MergeSort(num):
if(len(num)<=1): #递归边界条件
return num #到达边界时返回当前的子数组
mid = int(len(num)/2) #求出数组的中位数
llist,rlist = MergeSort(num[:mid]),MergeSort(num[mid:])#调用函数分别为左右数组排序
result = []
i,j = 0,0
while i < len(llist) and j < len(rlist): #while循环用于合并两个有序数组
if rlist[j]<llist[i]:
result.append(rlist[j])
j += 1
else:
result.append(llist[i])
i += 1
result += llist[i:]+rlist[j:] #把数组未添加的部分加到结果数组末尾
return result #返回已排序的数组
print(MergeSort(nums))Führen Sie das Programm aus und das Ausgabeergebnis lautet:
[1,2,3,4,5,6,7,8]
In der Funktion MergeSort() müssen zunächst die Randbedingungen beurteilt werden. Wenn ein Array, das nur ein Element enthält, als Funktionsparameter übergeben wird, existiert nur das Element im Array, sodass das Array seine Mindestgröße erreicht hat. Sobald Sie mit der Aufgabe der rekursiven Zerlegung eines Arrays fertig sind, bringen Sie das zerlegte Array einfach auf die vorherige Rekursionsebene zurück.
Wenn die Länge des unsortierten Arrays immer noch größer als 1 ist, verwenden Sie die Variable mid, um den mittleren Index des Arrays zu speichern und das unsortierte Array links und rechts in zwei Unterarrays aufzuteilen. Erstellen Sie dann zwei neue Arrays, um die sortierten linken und rechten Subarrays zu speichern. Hier wird die Idee der Rekursion verwendet. Wir stellen uns die Funktion MergeSort() nur als eine Funktion vor, die eine Liste sortiert, obwohl innerhalb der Funktion MergeSort() auch die Funktion selbst aufgerufen werden kann, um zwei Unterarrays zu sortieren.
Verwenden Sie anschließend eine While-Schleife, um die beiden bereits sortierten Arrays zusammenzuführen. Da die relative Größe der Elemente in den beiden Arrays nicht bestimmt werden kann, verwenden wir zwei Variablen, i und j, um die Positionen der Elemente zu markieren, die darauf warten, im linken Sub-Array bzw. im rechten Sub-Array hinzugefügt zu werden. Wenn die while-Schleife endet, verbleiben am Ende eines Subarrays möglicherweise einige größte Elemente, die nicht zur Ergebnisliste hinzugefügt wurden. Die Anweisung result+=llist[i:]+rlist[j:] dient daher dazu, diese Elemente zu verhindern davor, vermisst zu werden. Nachdem die Array-Zusammenführung abgeschlossen ist, gibt die Funktion ein geordnetes Array aus.
Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Merge-Sortieralgorithmus in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

