So rufen Sie die Methode der kleinsten Quadrate in Python auf und implementieren sie

Die sogenannte lineare Methode der kleinsten Quadrate kann als Fortsetzung der Lösung von Gleichungen verstanden werden. Der Unterschied besteht darin, dass ein unlösbares Problem entsteht, wenn die unbekannte Größe weitaus kleiner als die Anzahl der Gleichungen ist. Der Kern der Methode der kleinsten Quadrate besteht darin, unbekannten Zahlen Werte zuzuweisen und dabei den minimalen Fehler sicherzustellen.

Die Methode der kleinsten Quadrate ist ein sehr klassischer Algorithmus, und wir haben diesen Namen in der High School kennengelernt. Es ist ein äußerst häufig verwendeter Algorithmus. Ich habe zuvor über das Prinzip der linearen kleinsten Quadrate geschrieben und es in Python implementiert: kleinste Quadrate und seine Python-Implementierung und wie man nichtlineare kleinste Quadrate in Scipy aufruft: nichtlineare kleinste Quadrate (ergänzender Inhalt am Ende des Artikels) ; und Methode der kleinsten Quadrate für dünn besetzte Matrizen: Methode der kleinsten Quadrate mit dünn besetzter Matrix.

Im Folgenden wird die in Numpy und Scipy implementierte lineare Methode der kleinsten Quadrate beschrieben und die Geschwindigkeit der beiden verglichen.

Numpy-Implementierung

Die Methode der kleinsten Quadrate ist in Numpy implementiert, das heißt, lstsq(a,b) wird verwendet, um x ähnlich wie a@x=b zu lösen, wobei a eine Matrix von M×N ist M Reihen von Vektoren entsprechen genau der Lösung eines linearen Gleichungssystems. Wenn A für ein Gleichungssystem wie Ax=b eine vollstufige Simulation ist, kann es als x=A⁻¹b ausgedrückt werden, andernfalls kann es als x=(A^TA) ^{ausgedrückt werden −1}A ^Tb.

Wenn b eine Matrix von M×K ist, wird für jede Spalte ein Satz von x berechnet.

Es gibt 4 Rückgabewerte: das durch Anpassen erhaltene x, der Anpassungsfehler, der Rang der Matrix a und die einwertige Form der Matrix a.

import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.]

scipy-Paket

scipy.linalg bietet auch die Funktion der kleinsten Quadrate, der Funktionsname ist ebenfalls lstsq und die Parameterliste ist

lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

wobei a, b Ax=b ist, beide bieten überschreibbare Schalter, vorausgesetzt, Being True kann dies Sparen Sie Laufzeit. Darüber hinaus unterstützt die Funktion auch die Endlichkeitsprüfung, eine Option, die viele Funktionen in Linalg bieten. Sein Rückgabewert ist derselbe wie die Funktion der kleinsten Quadrate in Numpy.

cond ist ein Gleitkommaparameter, der den Schwellenwert für den singulären Wert angibt. Wenn der singuläre Wert kleiner als cond ist, wird er verworfen.

lapack_driver ist eine String-Option, die angibt, welche Algorithmus-Engine in LAPACK ausgewählt ist, optional „gelsd“, „gelsy“, „gelss“.

import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.]

Geschwindigkeitsvergleich

Machen Sie abschließend einen Geschwindigkeitsvergleich zwischen den beiden Sätzen der Kleinste-Quadrate-Funktionen

from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807

Dieses Mal gibt es keine große Lücke zwischen den beiden. Auch wenn die Matrixdimension auf 500 vergrößert wird zwei Es ist auch ein halbes Pfund.

N = 500
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173

Supplement

Python ruft die nichtlineare Methode der kleinsten Quadrate auf

Einführung und Konstruktor

In Scipy besteht der Zweck der nichtlinearen Methode der kleinsten Quadrate darin, eine Reihe von Funktionen zu finden, die die Summe der Quadrate minimieren Fehlerfunktion, kann als folgende Formel ausgedrückt werden

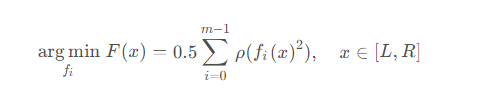
wobei ρ die Verlustfunktion darstellt, die als Vorverarbeitung von f_i(x) verstanden werden kann.

scipy.optimize kapselt die nichtlineare Funktion der kleinsten Quadrate, die als

least_squares(fun, x0, jac, bounds, method, ftol, xtol, gtol, x_scale, f_scale, loss, jac_sparsity, max_nfev, verbose, args, kwargs)

definiert ist. Unter diesen sind func und x0 erforderliche Parameter, func ist die zu lösende Funktion und x0 ist der Anfangswert der dort eingegebenen Funktion ist nein Der Standardwert ist ein Parameter, der eingegeben werden muss.

bound ist das Lösungsintervall, der Standardwert ist (−∞,∞). Wenn Verbose 1 ist, erfolgt eine Abschlussausgabe. Wenn Verbose 2 ist, werden während des Vorgangs weitere Informationen gedruckt. Darüber hinaus werden die folgenden Parameter zur Fehlerkontrolle verwendet, was relativ einfach ist.

	Standardwert	Bemerkungen
ftol	10-8	Funktionstoleranz
xtol	1 0-8	Unabhängige variable Toleranz
gtol	10-8	Gradiententoleranz
x_scale	1.0	Charakteristische Skala der Variablen
f_scale	1.0	Grenzwert des Restwerts

loss为损失函数，就是上面公式中的ρ \rhoρ，默认为linear，可选值包括

迭代策略

上面的公式仅给出了算法的目的，但并未暴露其细节。关于如何找到最小值，则需要确定搜索最小值的方法，method为最小值搜索的方案，共有三种选项，默认为trf

• trf：即Trust Region Reflective，信赖域反射算法

• dogbox：信赖域狗腿算法

• lm：Levenberg-Marquardt算法

这三种方法都是信赖域方法的延申，信赖域的优化思想其实就是从单点的迭代变成了区间的迭代，由于本文的目的是介绍scipy中所封装好的非线性最小二乘函数，故而仅对其原理做简略的介绍。

其中r为置信半径，假设在这个邻域内，目标函数可以近似为线性或二次函数，则可通过二次模型得到区间中的极小值点s_k。然后以这个极小值点为中心，继续优化信赖域所对应的区间。

雅可比矩阵

在了解了信赖域方法之后，就会明白雅可比矩阵在数值求解时的重要作用，而如何计算雅可比矩阵，则是接下来需要考虑的问题。jac参数为计算雅可比矩阵的方法，主要提供了三种方案，分别是基于两点的2-point；基于三点的3-point；以及基于复数步长的cs。一般来说，三点的精度高于两点，但速度也慢一倍。

此外，可以输入自定义函数来计算雅可比矩阵。

测试

最后，测试一下非线性最小二乘法

import numpy as np
from scipy.optimize import least_squares

def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + (1-np.cos((xs[i]*i)/5)*(i+1))
    return _sum

x0 = np.random.rand(5)
ret = least_squares(test, x0)
msg = f"最小值" + ", ".join([f"{x:.4f}" for x in ret.x])
msg += f"\nf(x)={ret.fun[0]:.4f}"
print(msg)
'''
最小值0.9557, 0.5371, 1.5714, 1.6931, 5.2294
f(x)=0.0000
'''

Das obige ist der detaillierte Inhalt vonSo rufen Sie die Methode der kleinsten Quadrate in Python auf und implementieren sie. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!