Prinzip und Implementierungsmethode des Java Bellman-Ford-Algorithmus

Ein Punkt

Wenn Sie auf eine negativ gewichtete Kante stoßen und es keine negative Schleife gibt (die Summe der Gewichte der Schleife ist negativ), können Sie den Bellman-Ford-Algorithmus verwenden, um den kürzesten Weg zu lösen. Der Vorteil dieses Algorithmus besteht darin, dass er den Fall negativer Variablengewichte verarbeiten kann und einfach zu implementieren ist. Sein Nachteil besteht jedoch darin, dass die zeitliche Komplexität zu hoch ist. Der Algorithmus kann jedoch auf verschiedene Weise optimiert werden, um die Effizienz zu steigern.

Der Bellman-Ford-Algorithmus ähnelt dem Dijkstra-Algorithmus, beide basieren auf Relaxationsoperationen. Der Dijkstra-Algorithmus verwendet eine gierige Methode, um den unverarbeiteten Knoten mit dem kleinsten Gewicht auszuwählen und ihn dann zu entspannen, während der Bellman-Ford-Algorithmus alle Kanten insgesamt n-1-mal entspannt. Wenn die n-te Operation noch entspannt werden kann, muss es eine negative Schleife geben, da die negative Schleife die Länge des kürzesten Pfads kontinuierlich verringern kann. Beträgt die Anzahl der Knoten n und die Anzahl der Kanten m, beträgt die maximale Laufzeit des Bellman-Ford-Algorithmus O(nm).

Zweite Algorithmusschritte

1 Datenstruktur

Da Kanten zur Entspannung verwendet werden müssen, wird Edge-Set-Array-Speicher verwendet. Jede Kante hat drei Domänen: zwei Endpunkte a und b und eine Kantengewichtung w

2 für alle Kanten j(a,b,w), wenn dis[e[j]b]> [j].a]+e[j].w, dann ist es entspannt und dis[e[j]b]=dis[e[j].a]+e[j].w. Unter diesen stellt dis[v] die kürzeste Pfadlänge vom Quellpunkt zum Knoten v dar.

3 Wiederholen Sie die Entspannungsoperation n-1 Mal.

4 Beurteilung der negativen Schleife.

Führen Sie die Entspannungsoperation erneut durch. Wenn sie immer noch entspannt werden kann, bedeutet dies, dass eine rechte negative Schleife vorliegt.

Drei Algorithmen-Implementierung

package graph.bellmanford;
 
import java.util.Scanner;
 
public class BellmanFord {
    static node e[] = new node[210];
    static int dis[] = new int[110];
    static int n;
    static int m;
    static int cnt = 0;
 
    static {
        for (int i = 0; i < e.length; i++) {
            e[i] = new node();
        }
    }
 
    static void add(int a, int b, int w) {
        e[cnt].a = a;
        e[cnt].b = b;
        e[cnt++].w = w;
    }
 
    static boolean bellman_ford(int u) { // 求源点 u 到其它顶点的最短路径长度，判负环
        for (int i = 0; i < dis.length; i++) {
            dis[i] = 0x3f;
        }
        dis[u] = 0;
        for (int i = 1; i < n; i++) { // 执行 n-1 次
            boolean flag = false;
            for (int j = 0; j < m; j++) // 边数 m 或 cnt
                if (dis[e[j].b] > dis[e[j].a] + e[j].w) {
                    dis[e[j].b] = dis[e[j].a] + e[j].w;
                    flag = true;
                }
            if (!flag)
                return false;
        }
        for (int j = 0; j < m; j++) // 再执行 1 次，还能松弛说明有环
            if (dis[e[j].b] > dis[e[j].a] + e[j].w)
                return true;
        return false;
    }
 
 
    static void print() { // 输出源点到其它节点的最短距离
        System.out.println("最短距离：");
        for (int i = 1; i <= n; i++)
            System.out.print(dis[i] + " ");
        System.out.println();
    }
 
    public static void main(String[] args) {
        int a, b, w;
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        for (int i = 0; i < m; i++) {
            a = scanner.nextInt();
            b = scanner.nextInt();
            w = scanner.nextInt();
            add(a, b, w);
        }
        if (bellman_ford(1)) // 判断负环
            System.out.println("有负环！");
        else
            print();
    }
}
 
class node {
    int a;
    int b;
    int w;
}

Vier Tests

1 Test ohne negative Schleife

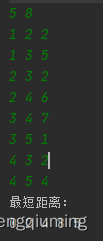2 Test mit negativer Schleife

Das obige ist der detaillierte Inhalt vonPrinzip und Implementierungsmethode des Java Bellman-Ford-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!