Heim >Backend-Entwicklung >Python-Tutorial >Handelsstrategien und Portfolioanalyse mit Python
Handelsstrategien und Portfolioanalyse mit Python
- 王林nach vorne
- 2023-05-18 13:13:062056Durchsuche
In diesem Artikel werden wir die Leistung von Handelsstrategien messen. Und wird eine einfache Momentum-Handelsstrategie entwickeln, die vier Anlageklassen nutzt: Anleihen, Aktien und Immobilien. Diese Anlageklassen weisen geringe Korrelationen auf, was sie zu hervorragenden Optionen für den Risikoausgleich macht.

Momentum-Handelsstrategie
Diese Strategie basiert auf Momentum, da Händler und Anleger sich seit langem der Auswirkungen von Momentum bewusst sind, die in einem breiten Spektrum von Märkten und Zeitrahmen zu beobachten sind. Wir nennen es also eine Momentum-Strategie. Trendfolge oder Time Series Momentum (TSM) ist ein anderer Name für die Verwendung dieser Strategien auf einem einzelnen Instrument. Wir werden eine grundlegende Momentum-Strategie erstellen und sie auf TCS testen, um zu sehen, wie sie funktioniert.
TSM-Strategieanalyse
Zuerst werden wir einige Bibliotheken importieren
import numpy as np import pandas as pd import matplotlib.pyplot as plt import yfinance as yf import ffn %matplotlib inline
Wir erstellen die grundlegende Momentum-Strategiefunktion TSMStrategy. Die Funktion gibt die erwartete Leistung über die logarithmische Rückgabe der Zeitreihe, den interessierenden Zeitraum und eine boolesche Variable zurück, die angibt, ob Shorting zulässig ist. Die Ausgabe der Funktion
def TSMStrategy(returns, period=1, shorts=False):
if shorts:
position = returns.rolling(period).mean().map(
lambda x: -1 if x <= 0 else 1)
else:
position = returns.rolling(period).mean().map(
lambda x: 0 if x <= 0 else 1)
performance = position.shift(1) * returns
return performance
ticker = 'TCS'
yftcs = yf.Ticker(ticker)
data = yftcs.history(start='2005-01-01', end='2021-12-31')
returns = np.log(data['Close'] / data['Close'].shift(1)).dropna()
performance = TSMStrategy(returns, period=1, shorts=False).dropna()
years = (performance.index.max() - performance.index.min()).days / 365
perf_cum = np.exp(performance.cumsum())
tot = perf_cum[-1] - 1
ann = perf_cum[-1] ** (1 / years) - 1
vol = performance.std() * np.sqrt(252)
rfr = 0.02
sharpe = (ann - rfr) / vol
print(f"1-day TSM Strategy yields:" +
f"nt{tot*100:.2f}% total returns" +
f"nt{ann*100:.2f}% annual returns" +
f"nt{sharpe:.2f} Sharpe Ratio")
tcs_ret = np.exp(returns.cumsum())
b_tot = tcs_ret[-1] - 1
b_ann = tcs_ret[-1] ** (1 / years) - 1
b_vol = returns.std() * np.sqrt(252)
b_sharpe = (b_ann - rfr) / b_vol
print(f"Baseline Buy-and-Hold Strategy yields:" +
f"nt{b_tot*100:.2f}% total returns" +
f"nt{b_ann*100:.2f}% annual returns" +
f"nt{b_sharpe:.2f} Sharpe Ratio")lautet wie folgt:
1-day TSM Strategy yields: -45.15% total returns -7.10% annual returns -0.17 Sharpe Ratio Baseline Buy-and-Hold Strategy yields: -70.15% total returns -13.78% annual returns -0.22 Sharpe Ratio
In Bezug auf angemessene jährliche Renditen übertrifft die 1-Tages-TSM-Strategie die Buy-and-Hold-Strategie. Da ein eintägiger Rückblick viele falsche Trends enthalten kann, haben wir verschiedene Zeiträume ausprobiert, um einen Vergleich zu sehen. Dabei wird das Modell 3, 5, 15, 30 und 90 Tage lang in einer Schleife ausgeführt.
import matplotlib.gridspec as gridspec
periods = [3, 5, 15, 30, 90]
fig = plt.figure(figsize=(12, 10))
gs = fig.add_gridspec(4, 4)
ax0 = fig.add_subplot(gs[:2, :4])
ax1 = fig.add_subplot(gs[2:, :2])
ax2 = fig.add_subplot(gs[2:, 2:])
ax0.plot((np.exp(returns.cumsum()) - 1) * 100, label=ticker, linestyle='-')
perf_dict = {'tot_ret': {'buy_and_hold': (np.exp(returns.sum()) - 1)}}
perf_dict['ann_ret'] = {'buy_and_hold': b_ann}
perf_dict['sharpe'] = {'buy_and_hold': b_sharpe}
for p in periods:
log_perf = TSMStrategy(returns, period=p, shorts=False)
perf = np.exp(log_perf.cumsum())
perf_dict['tot_ret'][p] = (perf[-1] - 1)
ann = (perf[-1] ** (1/years) - 1)
perf_dict['ann_ret'][p] = ann
vol = log_perf.std() * np.sqrt(252)
perf_dict['sharpe'][p] = (ann - rfr) / vol
ax0.plot((perf - 1) * 100, label=f'{p}-Day Mean')
ax0.set_ylabel('Returns (%)')
ax0.set_xlabel('Date')
ax0.set_title('Cumulative Returns')
ax0.grid()
ax0.legend()
_ = [ax1.bar(i, v * 100) for i, v in enumerate(perf_dict['ann_ret'].values())]
ax1.set_xticks([i for i, k in enumerate(perf_dict['ann_ret'])])
ax1.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['ann_ret'].keys()],
rotation=45)
ax1.grid()
ax1.set_ylabel('Returns (%)')
ax1.set_xlabel('Strategy')
ax1.set_title('Annual Returns')
_ = [ax2.bar(i, v) for i, v in enumerate(perf_dict['sharpe'].values())]
ax2.set_xticks([i for i, k in enumerate(perf_dict['sharpe'])])
ax2.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['sharpe'].keys()],
rotation=45)
ax2.grid()
ax2.set_ylabel('Sharpe Ratio')
ax2.set_xlabel('Strategy')
ax2.set_title('Sharpe Ratio')
plt.tight_layout()
plt.show()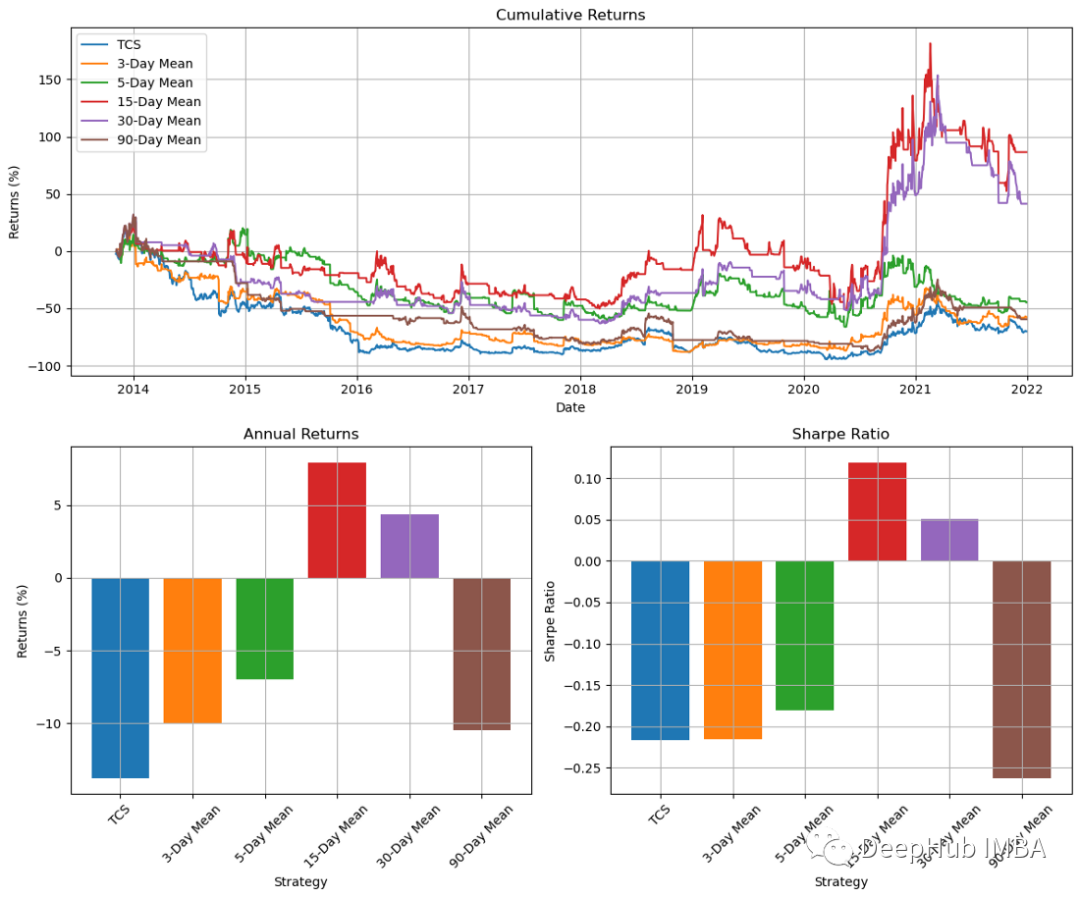
Wenn wir uns die Ergebnisse im Diagramm ansehen, können wir sehen, dass der 15-Tage-Momentum-Indikator die besten Ergebnisse liefert. Die Ergebnisse für andere Zeiträume sind jedoch gemischt. Dies zeigt, dass unsere Strategie nicht zuverlässig ist. Daher können wir den Handel auch beenden, indem wir einen Stop oder Trailing Stop in der Nähe der Spitze verwenden, anstatt dies zu tun, wenn der 15-Tage-Chart rückläufig oder flach ist.
Portfolioanalyse
Bisher haben wir eine Handelsstrategie in Python erstellt. Im Folgenden werden wir allgemeine Portfoliomerkmale messen und grafisch darstellen, um unsere Beobachtung und Analyse zu erleichtern.
Portfolioanalyse
Zunächst importieren wir einige wichtige Bibliotheken und beobachten die Leistung der Daten.
import pandas_datareader.data as web stocks = ['SPY','GLD','TLT','HYG'] data = web.DataReader(stocks,data_source='yahoo',start='01/01/2019')['Adj Close'] data.sort_index(ascending=True,inplace=True) perf = data.calc_stats() perf.plot()
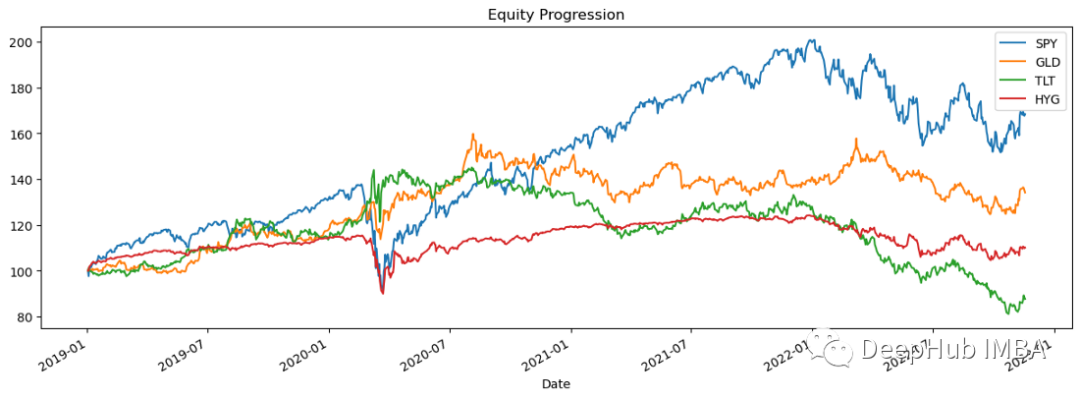
Log-Rendite
Log-Rendite wird zur Berechnung der exponentiellen Wachstumsrate verwendet. Anstatt die prozentuale Preisänderung für jeden Teilzeitraum zu berechnen, berechnen wir den organischen Wachstumsindex für diesen Zeitraum. Erstellen Sie zunächst eine DF, die die logarithmische Rendite jedes Aktienkurses in den Daten enthält, und erstellen Sie dann ein Histogramm für jede logarithmische Rendite.
returns = data.to_log_returns().dropna() print(returns.head()) Symbols SPY GLD TLT HYG Date 2019-01-03 -0.024152 0.009025 0.011315 0.000494 2019-01-04 0.032947 -0.008119 -0.011642 0.016644 2019-01-07 0.007854 0.003453 -0.002953 0.009663 2019-01-08 0.009351 -0.002712 -0.002631 0.006470 2019-01-09 0.004663 0.006398 -0.001566 0.001193
Das Histogramm sieht wie folgt aus:
ax = returns.hist(figsize=(20, 10),bins=30)
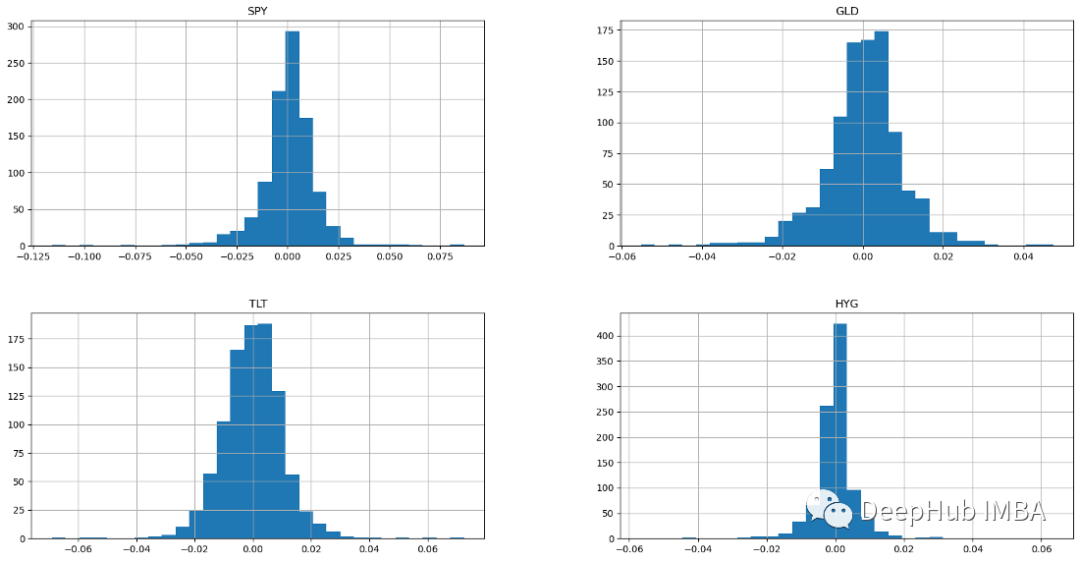
Alle vier Anlageklassen zeigen Histogramme der Normalverteilung. Eine Stichprobe mit einer Normalverteilung hat ein arithmetisches Mittel und eine Gleichverteilung über und unter dem Mittelwert (die Normalverteilung, auch Gaußsche Verteilung genannt, ist symmetrisch). Wenn die Renditen normalverteilt sind, wird erwartet, dass mehr als 99 % der Renditen innerhalb von drei Standardabweichungen vom Mittelwert liegen. Diese glockenförmigen Normalverteilungsmerkmale ermöglichen es Analysten und Anlegern, bessere statistische Rückschlüsse auf die erwarteten Renditen und Risiken einer Aktie zu ziehen. Aktien mit einer Glockenkurve sind typischerweise Blue Chips mit geringer und vorhersehbarer Volatilität.
Maximale Retracement-Rate DRAWDOWN
DRAWDOWN bezieht sich auf den Wert, der auf ein relatives Tief fällt. Dies ist ein wichtiger Risikofaktor, den Anleger berücksichtigen sollten. Lassen Sie uns eine visuelle Darstellung der abnehmenden Strategie zeichnen.
ffn.to_drawdown_series(data).plot(figsize=(15,10))
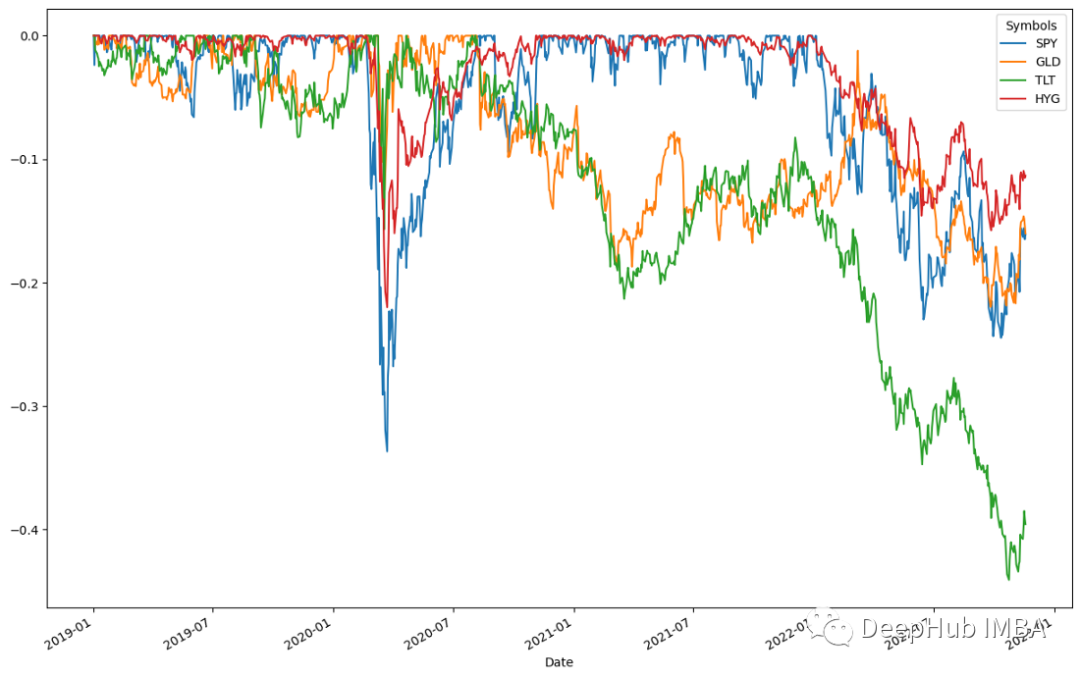
Alle vier Vermögenswerte gingen im ersten Halbjahr 2020 zurück, wobei SPY mit 0,5 % den größten Rückgang verzeichnete. Dann, im ersten Halbjahr 2020, erholten sich alle Vermögenswerte sofort. Dies deutet auf eine hohe Vermögensrückgewinnungsrate hin. Diese Vermögenswerte erreichten etwa im Juli 2020 ihren Höhepunkt. Diesem Trend folgend verzeichneten alle Anlageklassen leichte Rückgänge, sobald die Erholung ihren Höhepunkt erreichte. Den Ergebnissen zufolge wird TLT im zweiten Halbjahr 2022 den größten Rückgang von 0,5 % verzeichnen, bevor es sich Anfang 2023 erholt.
MARKOWITZ Mean-Varianz-Optimierung
Im Jahr 1952 schlug Markowitz die Mean-Varianz-Portfoliotheorie vor, auch bekannt als moderne Portfoliotheorie. Anleger können diese Konzepte nutzen, um ein Portfolio aufzubauen, das die erwarteten Renditen basierend auf einem bestimmten Risikoniveau maximiert. Basierend auf der Markowitz-Methode können wir ein „optimales Portfolio“ generieren.
returns.calc_mean_var_weights().as_format('.2%')
#结果
SPY 46.60%
GLD 53.40%
TLT 0.00%
HYG 0.00%
dtype: objectKorrelationsstatistik
Korrelation ist eine statistische Methode zur Messung der Beziehung zwischen Wertpapieren. Diese Informationen lassen sich am besten mithilfe von Heatmaps anzeigen. Mithilfe von Heatmaps können wir Korrelationen zwischen Wertpapieren erkennen.
returns.plot_corr_heatmap()
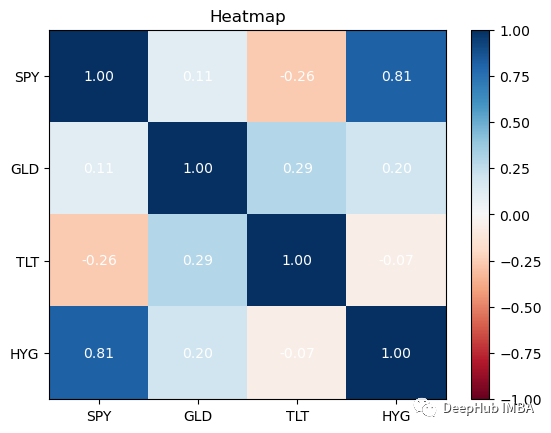
最好在你的投资组合中拥有相关性较低的资产。除了SPY与HYG,这四个资产类别的相关性都很低,这对我们的投资组合是不利的:因为如果拥有高度相关的不同资产组,即使你将风险分散在它们之间,从投资组合构建的角度来看,收益也会很少。
总结
通过分析和绘制的所有数据进行资产配置,可以建立一个投资组合,极大地改变基础投资的风险特征。还有很多我没有提到的,但可以帮助我们确定交易策略价值的起点。我们将在后续文章中添加更多的技术性能指标。
Das obige ist der detaillierte Inhalt vonHandelsstrategien und Portfolioanalyse mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

