So implementieren Sie die zehn besten Sortieralgorithmen in Java

Stabilität des Sortieralgorithmus:

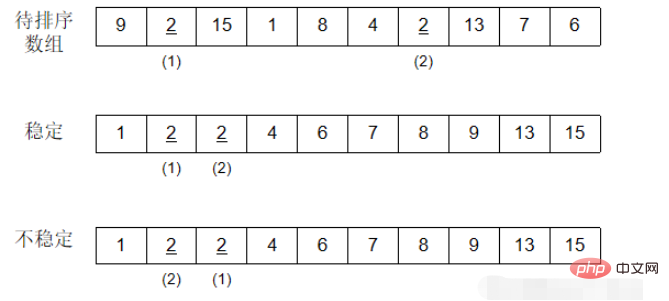
Angenommen, es gibt mehrere Datensätze mit demselben Schlüsselwort in der zu sortierenden Datensatzsequenz. Wenn danach Beim Sortieren wird garantiert, dass die relative Reihenfolge dieser Datensätze unverändert bleibt, d Wenn [i] nach der vorherigen Sortierung von a[j] immer noch vorhanden ist, wird der Sortieralgorithmus als stabil bezeichnet; andernfalls wird er als instabil bezeichnet.

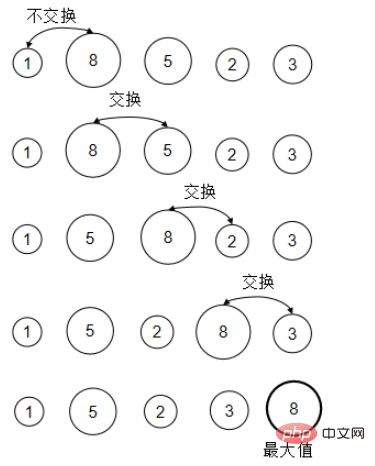
1. Auswahlsortierung

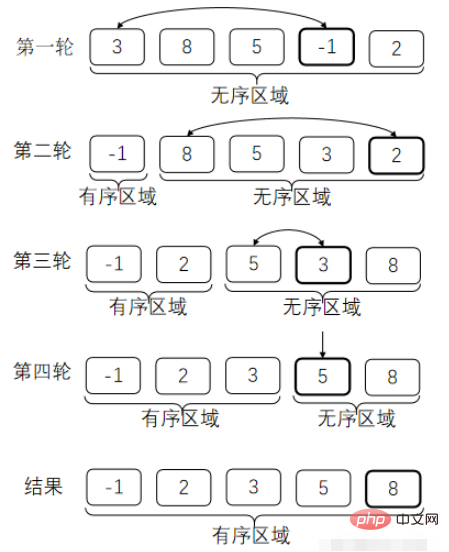
Wählen Sie jedes Mal das kleinste Element aus den zu sortierenden Elementen aus und fügen Sie dann das 1. hinzu und 1. Elemente der Reihe nach werden die Elemente an den Positionen 2, 3... vertauscht. Dadurch entsteht ein geordneter Bereich an der Vorderseite des Arrays. Bei jedem Austausch wird die Länge der geordneten Region um eins erhöht.

public static void selectionSort(int[] arr){
    //细节一：这里可以是arr.length也可以是arr.length-1
    for (int i = 0; i < arr.length-1 ; i++) {
        int mini = i;
        for (int j = i+1; j < arr.length; j++) {
            //切换条件，决定升序还是降序
            if(arr[mini]>arr[j]) mini =j;
        }
        swap(arr,mini,i);
    }
}

2. Blasensortierung

Vergleichen Sie zwei benachbarte Zahlen der Reihe nach und tauschen Sie sie aus, wenn die Reihenfolge falsch ist. Komm her In diesem Fall können Sie nach jeder Vergleichsrunde die größte Zahl dort platzieren, wo sie sein sollte. (Es ist, als würde man die größte Blase zur obersten Ebene bringen.)#🎜🎜 ## 🎜🎜#Hier soll die Bedeutung der falschen Reihenfolge erklärt werden. Wir sortieren in aufsteigender Reihenfolge. Die späteren Werte sollten größer oder gleich den vorherigen Werten sein.

public static void bubbleSort(int[] arr){
    for (int i = 0; i < arr.length-1; i++) {
        //记录本次有没有进行交换的操作
        boolean flag = false;
        //保存在头就动头，保存在尾就动尾
        for(int j =0 ; j < arr.length-1-i ; j++){
            //升序降序选择地
            if(arr[j] > arr[j+1])
            {
                swap(arr,j,j+1);
                flag = true;
            }
        }
        //如果本次没有进行交换操作，表示数据已经有序
        if(!flag){break;} //程序结束
    }
}

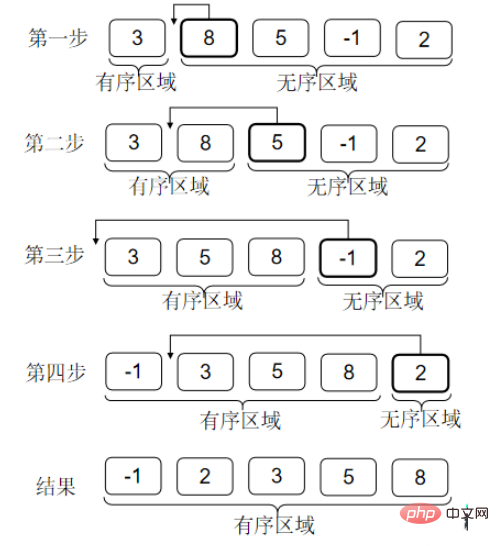
3. Einfügungssortierung

Einfügungssortierung kann eigentlich als der Prozess des Kartenziehens beim Pokern verstanden werden. Wenn Sie die Karten berühren, sind die Karten in Ihrer Hand immer in Ordnung. Jedes Mal, wenn Sie eine Karte berühren, stecken Sie die Karte dort ein, wo sie sein sollte. Nachdem alle Karten berührt wurden, sind alle Karten in Ordnung.

Denken: Vor dem Array wird ein geordneter Bereich gebildet. Wenn ich dann nach der Position suche, an der die aktuelle Nummer eingefügt werden soll, kann ich Verwenden Sie dazu die binäre Division. Wurde die Komplexität der Einfügungssortierung auf O(nlogn) optimiert?

                                                                                                                                                                     Die Position kann anhand der Komplexität des Protokolls ermittelt werden. Der Schlüssel liegt darin, dass, wenn Sie ein Array zum Speichern der Daten verwenden, die Komplexität des Zurückschiebens der Daten während des Einfügens immer noch O(n) beträgt. Wenn Sie eine verknüpfte Liste verwenden, ist das Finden und Einfügen der Position O (1), die verknüpfte Liste kann jedoch nicht in zwei Teile geteilt werden.

public static void insertSort(int[] arr){
        //从第二个数开始，把每个数依次插入到指定的位置
        for(int i = 1 ; i < arr.length ; i++)
        {
            int key = arr[i];
            int j = i-1;
            //大的后移操作
            while(j >= 0 && arr[j] > key)
            {
                arr[j+1] = arr[j];
                j--;
            }
            arr[j+1] = key;
        }
    }

4. Hill-Sortierung

Hill-Sortierung ist ein Sortieralgorithmus, der 1959 von Donald Shell vorgeschlagen wurde. Es handelt sich um eine verbesserte und effiziente Version der Direkteinfügungssortierung. Die Hill-Sortierung erfordert die Vorbereitung eines Datensatzes als inkrementelle Sequenz.

Dieser Datensatz muss die folgenden drei Bedingungen erfüllen:

1 Die Daten sind in absteigender Reihenfolge angeordnet

2 in den Daten ist kleiner als das zu sortierende Array. Die Länge von

3 Der Mindestwert in den Daten ist 1.

Solange das Array die oben genannten Anforderungen erfüllt, kann es als inkrementelle Sequenz verwendet werden. Unterschiedliche inkrementelle Sequenzen wirken sich jedoch auf die Sortiereffizienz aus. Hier verwenden wir {5,3,1} als inkrementelle Sequenz, um

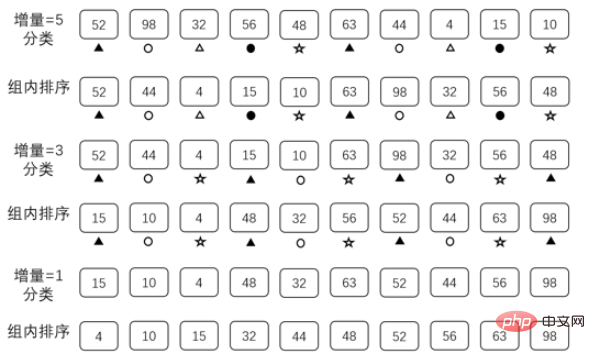zu erklären. Der Grund für die Optimierung: Reduzieren Sie die Datenmenge und machen Sie O( n) und O(n^2) sind nicht groß.

Sie können den Maximal-/Minimalwert in O(1) nehmen, den Maximal-/Minimalwert in O(logn) löschen und Elemente einfügen in O(logn)

MIN-HEAPIFY (i ) Operation:

Wir gehen davon aus, dass der linke Teilbaum und der rechte Teilbaum eines Knotens i im vollständigen Binärbaum beide die erfüllen Eigenschaften eines kleinen Root-Heaps. Nehmen Sie an, dass das linke Kind des i-Knotens left_i und das rechte Kind des i-Knotens rigℎt_i ist. Wenn a[i] größer als a[left_i] oder a[rigℎt_i] ist, erfüllt der gesamte Teilbaum mit i-Knoten als Wurzelknoten nicht die Eigenschaften eines kleinen Wurzelheaps. Wir müssen jetzt eine Operation ausführen: setze i als Wurzelknoten Der Teilbaum des Wurzelknotens wird in einen kleinen Wurzelheap angepasst.

public static void shellSort(int[] arr){
        //分块处理
        int gap = arr.length/2; //增量
        while(1<=gap)
        {
            //插入排序：只不过是与增量位交换
            for(int i = gap ; i < arr.length ; i++)
            {
                int key = arr[i];
                int j = i-gap;
                while(j >= 0 && arr[j] > key)
                {
                    arr[j+gap] = arr[j];
                    j-=gap;
                }
                arr[j+gap] = key;
            }
            gap = gap/2;
        }
    }

Ich verwende einen großen Wurzelstapel: zuerst die linke Wurzel und dann die rechte Wurzel (sehen Sie, wie Sie es schreiben). ) - >Jede Wurzel geht nach oben und unten. (Links, rechts, oben und unten)

6. Zusammenführungssortierung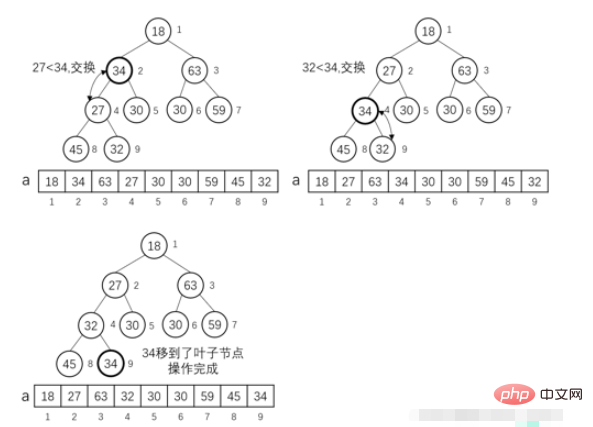

Zusammenführungssortierung ist eine typische Anwendung der Divide-and-Conquer-Methode. Lassen Sie uns zunächst die Divide-and-Conquer-Methode vorstellen. Und-Herrsche-Methode Die Teile-und-Herrsche-Methode besteht darin, ein komplexes Problem in zwei oder mehr identische oder ähnliche Teilprobleme zu teilen, und dann werden die Teilprobleme in kleinere Teilprobleme unterteilt ... bis die Das letzte Teilproblem ist klein genug, um direkt gelöst zu werden. Anschließend werden die Lösungen der Teilprobleme kombiniert, um eine Lösung für das ursprüngliche Problem zu erhalten.

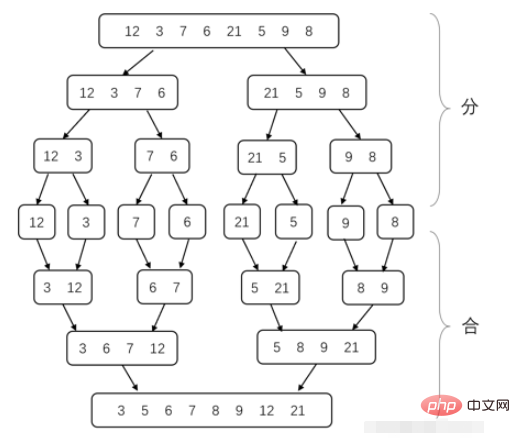
Der Prozess des Unterproblems der Merge-Sort-Zerlegung besteht darin, das Array jedes Mal in zwei Teile zu teilen, bis die Länge des Arrays 1 beträgt (da ein Array mit nur einer Zahl geordnet ist). Fügen Sie dann benachbarte geordnete Arrays zu einem geordneten Array zusammen. Bis sie alle zusammengesetzt sind, wird das gesamte Array sortiert. Das nun zu lösende Problem besteht darin, zwei geordnete Arrays zu einem geordneten Array zusammenzuführen. Tatsächlich geht es darum, jedes Mal die beiden kleinsten aktuellen Elemente der beiden Arrays zu vergleichen. Wählen Sie das kleinere aus Antwort Array

public static void mergeSort(int[] arr, int low, int high){
        int middle = (high + low)/2;
        if (low < high){
            //递归排序左边
            mergeSort(arr, low, middle);
            //递归排序右边
            mergeSort(arr, middle +1, high);
            //将递归排序好的左右两边合并
            merge(arr, low, middle, high);
        }
 
    }
 
    public static void merge(int[] arr, int low, int middle, int high){
        //存储归并后的临时数组
        int[] temp = new int[high - low + 1];
        int i = low;
        int j = middle + 1;
        //记录临时数组中存放数字的下标
        int index = 0;
        while (i <= middle && j <= high){
            if (arr[i] < arr[j]){
                temp[index] = arr[i];
                i++;
            } else {
                temp[index] = arr[j];
                j++;
            }
            index++;
        }
        //处理剩下的数据
        while (j <= high){
            temp[index] = arr[j];
            j++;
            index++;
        }
        while (i <= middle){
            temp[index] = arr[i];
            i++;
            index++;
        }
        //将临时数组中的数据放回原来的数组
        for (int k = 0; k < temp.length; ++k){
            arr[k + low] = temp[k];
        }
    }

七.快速排序

        快速排序的工作原理是：从待排序数组中随便挑选一个数字作为基准数，把所有比它小的数字放在它的左边，所有比它大的数字放在它的右边。然后再对它左边的数组和右边的数组递归进行这样的操作。

        全部操作完以后整个数组就是有序的了。 把所有比基准数小的数字放在它的左边，所有比基准数大的数字放在它的右边。这个操作，我们称为“划分”(Partition)。

	//快速排序
	public static void QuickSort1(int[] arr, int start, int end){
		int low = start, high = end;
		int temp;
		if(start < end){
		    int guard = arr[start];
			while(low != high){
				while(high > low && arr[high] >= guard) high--;
				while(low < high && arr[low] <= guard) low++;
				if(low < high){
					temp = arr[low];
					arr[low] = arr[high];
					arr[high] = temp;
				}
			}
			arr[start] = arr[low];
			arr[low] = guard;
			QuickSort1(arr, start, low-1);
			QuickSort1(arr, low+1, end);
		}
	}
	
	//快速排序改进版(填坑法)
	public static void QuickSort2(int[] arr, int start, int end){
		int low = start, high = end;
		if(start < end){
		while(low != high){
	    	int guard = arr[start];//哨兵元素
			while(high > low && arr[high] >= guard) high--;
			arr[low] = arr[high];
			while(low < high && arr[low] <= guard) low++;
			arr[high] = arr[low];
		}
		arr[low] = guard;
		QuickSort2(arr, start, low-1);
		QuickSort2(arr, low+1, end);
	}
}

八.鸽巢排序

        计算一下每一个数出现了多少次。举一个例子，比如待排序的数据中1出现了2次，2出现了0次，3出现了3次，4出现了1次，那么排好序的结果就是{1.1.3.3.3.4}。

//鸽巢排序
    public static void PigeonholeSort(int[] arr){
        //获取最大值
        int k = 0;
        for (int i = 0; i < arr.length; i++) {
            k = Math.max(k,arr[i]);
        }
        //创建计数数组并且初始化为0
        int[] cnt = new int[k+10];
        for(int i = 0 ; i <= k ; i++) { cnt[i]=0; }
        for(int i = 0 ; i < arr.length ;i++) { cnt[arr[i]]++; }
        int j = 0;
        for(int i = 0 ; i <=k ; i++)
        {
            while(cnt[i]!=0)
            {
                arr[j]=i;
                j++;
                cnt[i]--;
            }
        }
    }

        鸽巢排序其实算不上是真正意义上的排序算法，它的局限性很大。只能对纯整数数组进行排序，举个例子，如果我们需要按学生的成绩进行排序。是一个学生+分数的结构那就不能排序了。

九.计数排序

        先考虑这样一个事情：如果对于待排序数据中的任意一个元素 a[i]，我们知道有 m 个元素比它小，那么我们是不是就可以知道排好序以后这个元素应该在哪个位置了呢？（这里先假设数据中没有相等的元素）。计数排序主要就是依赖这个原理来实现的。

比如待排序数据是{2,4,0,2,4} 先和鸽巢一样做一个cnt数组{1,0,2,0,2}                                                                                                                                    0,1,2,3,4

此时cnt[i]表示数据i出现了多少次，

然后对cnt数组做一个前缀和{1,1,3,3,5}    ：0,1,2,3,4

此时cnt[i]表示数据中小于等于i的数字有多少个

2,5,7	1,3,4	1 & lt; 2, nehmen Sie 1 und bewegen Sie den Zeiger von Array B nach hinten	1
2,5,7	1,3,4	2	1,2
2,5 ,7	1,3, 4	3	1,2,3
2,5,7 1,3,4	1,3,4	array Es gibt keine Elemente in b, nimm 5	1,2,3,4,5
2,5,7	1 ,3,4	Es gibt keine Elemente in Array b Ja, nimm 7	1,2,3,4,5,7

待排序数组	计数数组	说明	答案数组ans
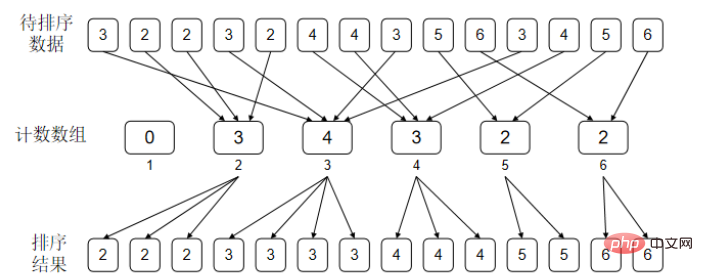
2,4,0,2,4	1,1,3,3,5	初始状态	null,null,null,null,null,
2,4,0,2,4	1,1,3,3,5	cnt[4]=5，ans第5位赋值，cnt[4]-=1	null,null,null,null,4
2,4,0,2,4	1,1,3,3,4	cnt[2]=3，ans第3位赋值，cnt[2]-=1	null,null,2 null,4
2,4,0,2,4	1,1,2,3,4	cnt[0]=1，ans第1位赋值，cnt[0]-=1	0,null,2,null,4
2,4,0,2,4	0,1,2,3,4	cnt[4]=4，ans第4位赋值，cnt[4]-=1	0,null,2,4,4
2,4,0,2,4	0,1,2,3,3	cnt[2]=2，ans第2位赋值，cnt[2]-=1	0,2,2,4,4

十.基数排序

基数排序是通过不停的收集和分配来对数据进行排序的。

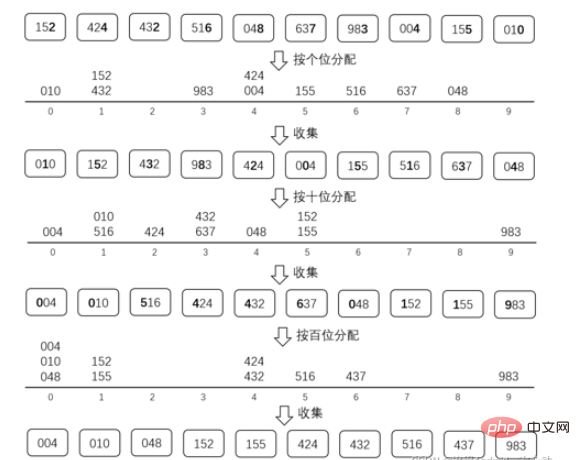
• 因为是10进制数，所以我们准备十个桶来存分配的数。

• 最大的数据是3位数，所以我们只需要进行3次收集和分配。

• 需要先从低位开始收集和分配（不可从高位开始排，如果从高位开始排的话，高位排好的顺序会在排低位的时候被打乱，有兴趣的话自己手写模拟一下试试就可以了）

• 在收集和分配的过程中，不要打乱已经排好的相对位置

        比如按十位分配的时候，152和155这两个数的10位都是5，并且分配之前152在155的前面，那么收集的时候152还是要放在155之前的。

//基数排序
    public static void radixSort(int[] array) {
        //基数排序
        //首先确定排序的趟数;
        int max = array[0];
        for (int i = 1; i < array.length; i++) {
            if (array[i] > max) {
                max = array[i];
            }
        }
        int time = 0;
        //判断位数;
        while (max > 0) {
            max /= 10;
            time++;
        }
        //建立10个队列;
        List<ArrayList> queue = new ArrayList<ArrayList>();
        for (int i = 0; i < 10; i++) {
            ArrayList<Integer> queue1 = new ArrayList<Integer>();
            queue.add(queue1);
        }
        //进行time次分配和收集;
        for (int i = 0; i < time; i++) {
            //分配数组元素;
            for (int j = 0; j < array.length; j++) {
                //得到数字的第time+1位数;
                int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
                ArrayList<Integer> queue2 = queue.get(x);
                queue2.add(array[j]);
                queue.set(x, queue2);
            }
            int count = 0;//元素计数器;
            //收集队列元素;
            for (int k = 0; k < 10; k++) {
                while (queue.get(k).size() > 0) {
                    ArrayList<Integer> queue3 = queue.get(k);
                    array[count] = queue3.get(0);
                    queue3.remove(0);
                    count++;
                }
            }
 
        }
 
 
    }

Das obige ist der detaillierte Inhalt vonSo implementieren Sie die zehn besten Sortieralgorithmen in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!