Heim >Java >javaLernprogramm >So analysieren Sie das Problem des Turms von Hanoi mit Java
So analysieren Sie das Problem des Turms von Hanoi mit Java
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-05-14 23:16:041261Durchsuche
1. Ursache des Turm-von-Hanoi-Problems
Der Turm von Hanoi, auch bekannt als der Turm von Hanoi, ist ein Lernspielzeug, das seinen Ursprung in alten indischen Legenden hat. Als Brahma die Welt erschuf, schuf er drei Diamantsäulen. Auf einer Säule wurden 64 Goldscheiben in der Reihenfolge ihrer Größe von unten nach oben gestapelt. Brahma befahl dem Brahmin, die Scheiben auf einer anderen Säule in der Reihenfolge ihrer Größe von unten neu anzuordnen. Und es ist festgelegt, dass die Festplatte auf der kleinen Festplatte nicht vergrößert werden kann und jeweils nur eine Festplatte zwischen den drei Säulen bewegt werden kann

2. Problemanalyse
Beginnen Sie mit einem einfachen Problem
Überlegen Sie einfach 64 Teller. Es kann schwierig sein, wir können mit 1 Teller beginnen, wie unten gezeigt:
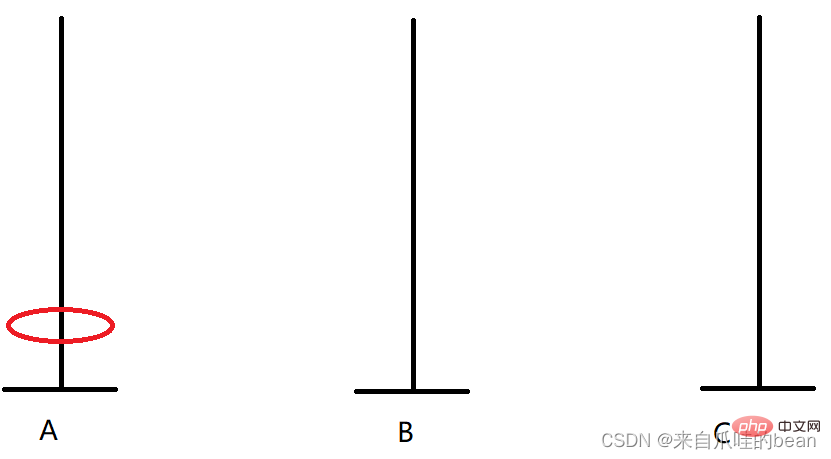 A -> C
A -> C
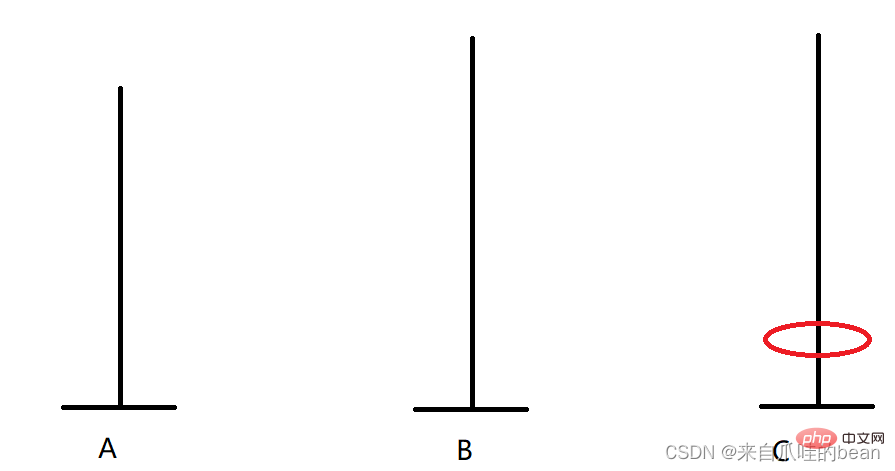 Wenn es nur einen Teller gibt, können wir direkt A platzieren auf der Säule Die Platte wird zur C-Säule verschoben
Wenn es nur einen Teller gibt, können wir direkt A platzieren auf der Säule Die Platte wird zur C-Säule verschoben
Es muss einmal verschoben werden
Zwei Platten
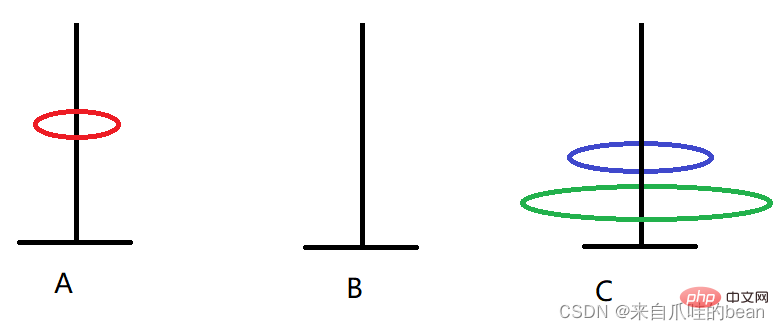
Wenn es zwei Platten gibt, können wir es auch auf folgende Weise erreichen:
A -> >C B-> C
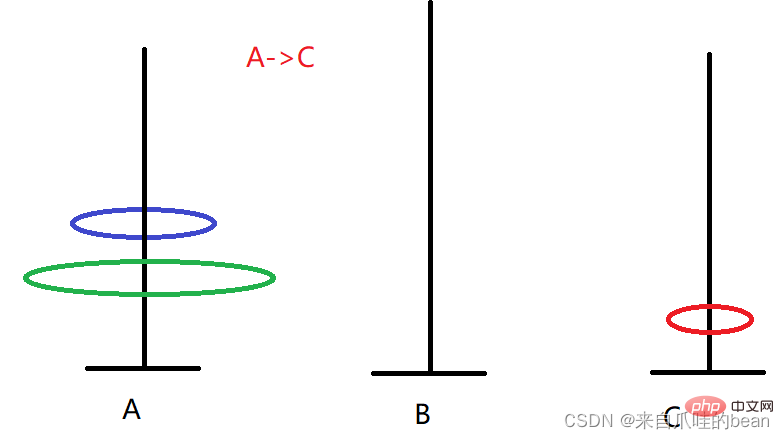
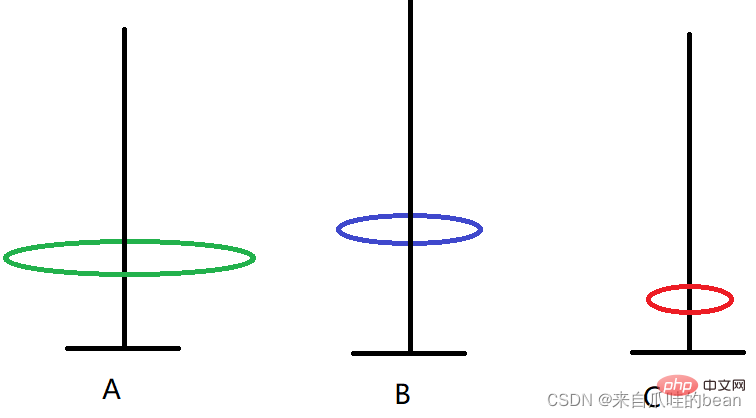
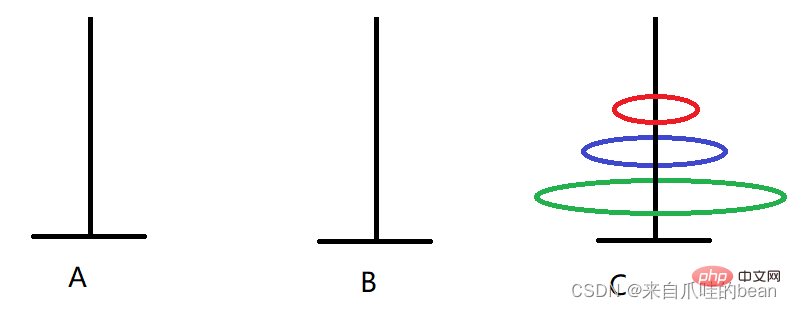
1. A -> Drei Teller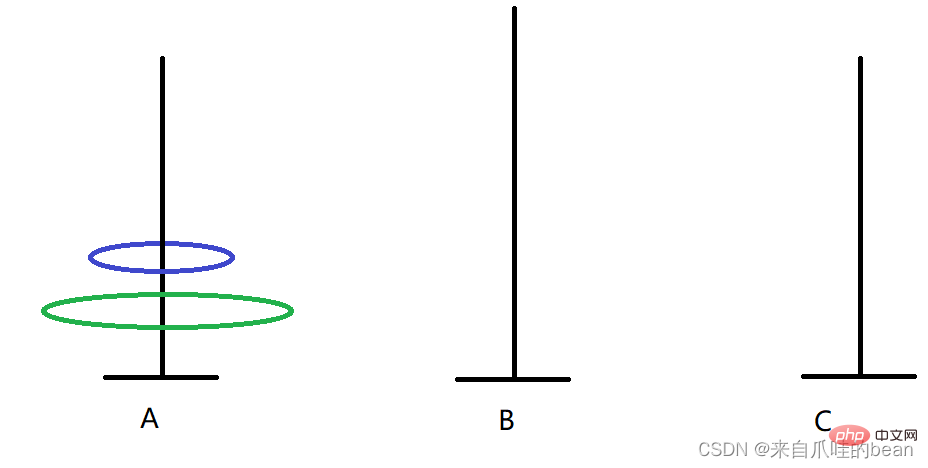 Die Bewegungsschritte sind wie folgt:
Die Bewegungsschritte sind wie folgt:
A -> B A -> C A ->
1. A -> C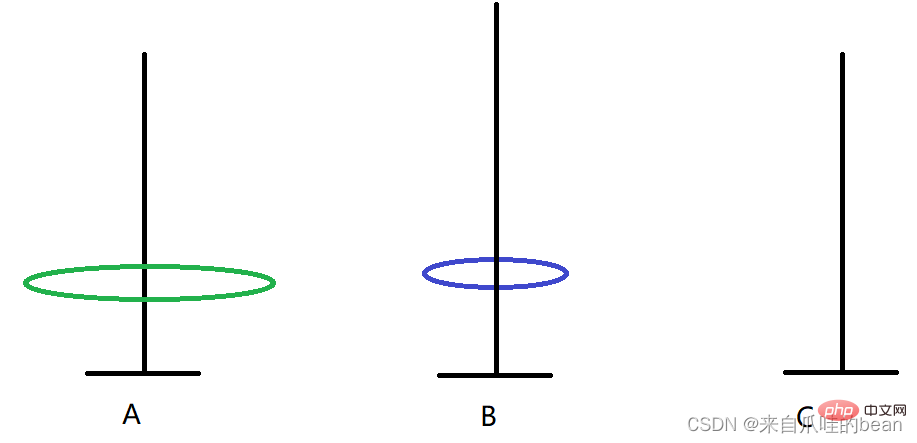
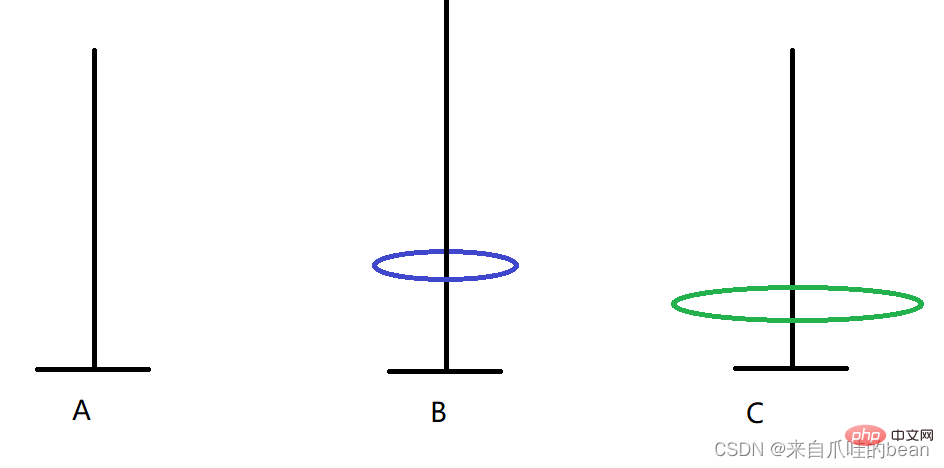
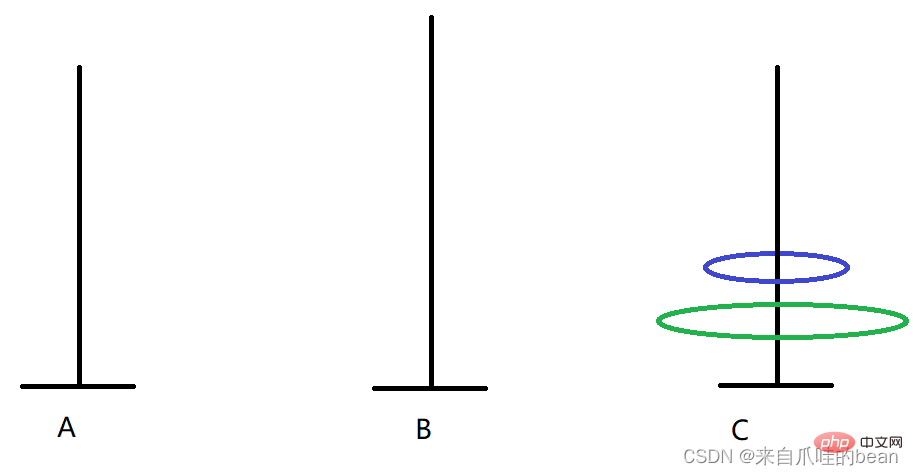
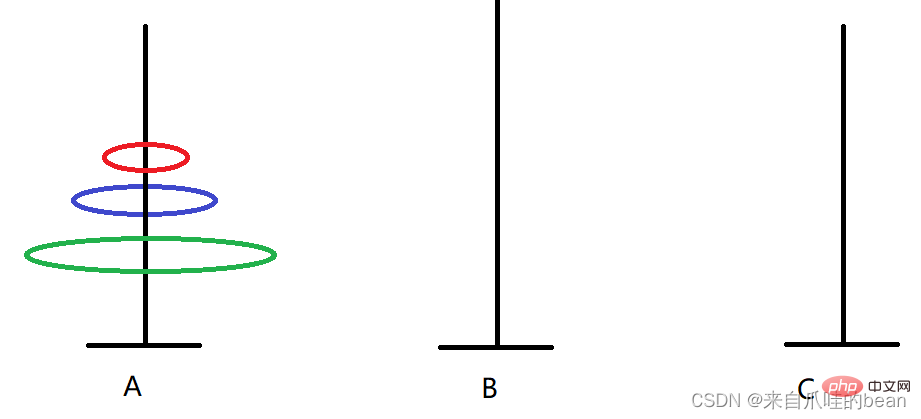 2 Platten 3 Mal bewegen
2 Platten 3 Mal bewegen
3 Platten 7 Mal bewegen
......
 3. Lösung des Problems
3. Lösung des Problems
Wir können dieses Problem durch Rekursion lösen und das richtige Verfahren erhalten, wie man sich bewegt
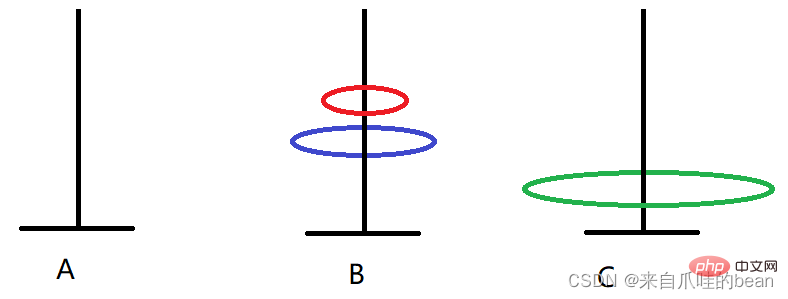
Wie bewegt man sich, wenn es N Platten gibt? 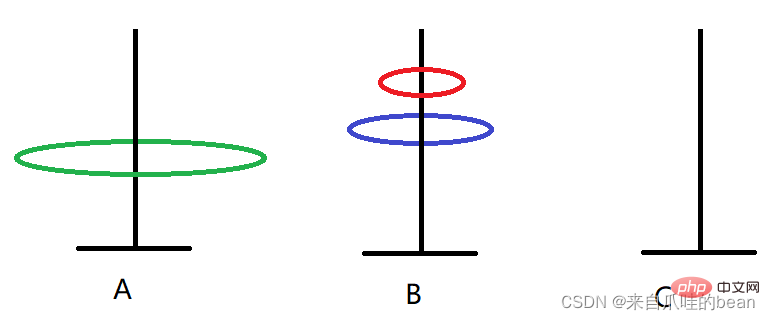
 Laden Sie den Code hoch
Laden Sie den Code hoch
public static void hanoi(int num, String src, String help, String dest) {
if (num == 1) { // 只有一个盘子的时候直接移动
System.out.print(src + "->" + dest + " "); // 将一个盘子从源柱子挪到目标柱子
} else {
hanoi(num - 1, src, dest, help); // 将n - 1个盘子从源柱子借助目标柱子挪到辅助柱子
System.out.print(src + "->" + dest + " "); // 将一个盘子从源柱子挪到目标柱子
hanoi(num - 1, help, src, dest); // 将辅助柱子上n - 1个盘子借助源柱子挪到目标柱子
}
}
public static void main(String[] args) {
hanoi(3, "A", "B", "C");
}In diesem Code ist src die Quelle Säule, Hilfe ist die Hilfssäule und Ziel ist die Zielsäule
Dies ist eine Zwei-Wege-Rekursion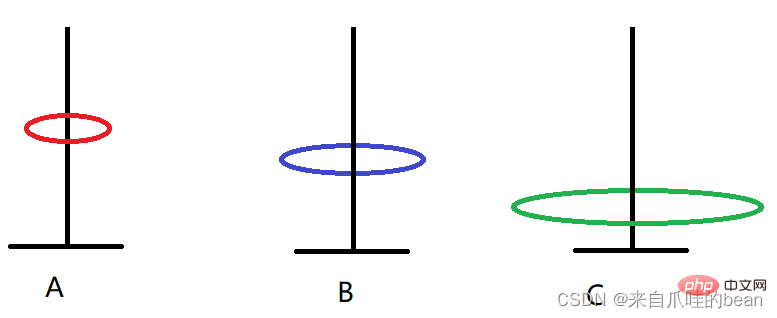
 Wie lange dauert es, 64 Teller zu bewegen
Wie lange dauert es, 64 Teller zu bewegen
Hier gehen wir davon aus, dass Brahmanen sehr schlau sind und sofort wissen, wie man sich richtig bewegt, ohne nachzudenken. Es dauert eine Sekunde, um einen Teller zu bewegen und weiterzumachen
Die Umrechnung von 2^64 - 1 Sekunde in ein Jahr entspricht etwa 5849 4241 7355 Jahren (584,942 Milliarden Jahren), und die Erde existiert erst seit 4,5 Milliarden Jahren, und die erwartete Lebensdauer des Sonnensystems soll mehrere zehn Milliarden Jahre betragen Jahre. Es sind tatsächlich 584,942 Milliarden Jahre vergangen, ganz zu schweigen vom Sonnensystem und der Milchstraße, zumindest ist alles Leben auf der Erde, einschließlich der Vatikanischen Türme, Tempel usw., längst ausgelöscht.
Verwandte Prophezeiungen
Es gibt eine Prophezeiung, dass das Universum blitzschnell zerstört wird, wenn dieses Ding fertiggestellt ist. Manche Leute glauben auch, dass Brahmanen die Scheiben immer noch ständig bewegen
Wie lange dauert es, bis der Computer 64 Platten bewegt?
Die Kernfrequenz meines Computers beträgt 2,90 GHz, was 2,9 Milliarden Operationen pro Sekunde entspricht. Die erforderliche Zeit, um 2^64 - 1 Mal zu bewegen, beträgt also etwa 201 Jahre
Das obige ist der detaillierte Inhalt vonSo analysieren Sie das Problem des Turms von Hanoi mit Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

