So zeichnen Sie in Python ein Doppelkreisdiagramm mit Verbindungslinien

1. Importieren Sie die erforderlichen Bibliotheken

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import ConnectionPatch
from matplotlib import cm

Mit der ConnectionPatch-Klasse im Modul matplotlib.patches können Sie die Verbindung zwischen zwei Unterplots zeichnen. In Visualisierungen wie einem Doppelkreisdiagramm können Sie diese Klasse verwenden, um eine Verbindung zwischen zwei Untergraphen zu zeichnen und so die Beziehung zwischen ihnen auszudrücken. Diese Klasse stellt viele Parameter und Methoden bereit, mit denen Eigenschaften wie Stil und Position der Verbindung gesteuert werden können.

ConnectionPatch wird zum Hinzufügen von Verbindungen in Matplotlib verwendet. Seine Hauptparameter sind wie folgt:

• xyA: der Startpunkt der Verbindungslinie;

• coordsA: das Koordinatensystem des Startpunkts, Standard ist Daten;

• coordsB: Koordinatensystem des Endpunkts, Standard ist Daten;

• axesB: Achsenobjekt, an dem sich der Endpunkt befindet;

• Farbe: die Farbe der Verbindungslinie;

• Linienstil: der Linienstil der Verbindungslinie.

• Zu den häufig verwendeten Methoden von ConnectionPatch gehören:

• set_color: Legen Sie die Farbe der Verbindungslinie fest;

• set_linewidth: Legen Sie die Linienbreite fest die Verbindungslinie;

set_linestyle: Legt den Linienstil der Verbindungslinie fest.

• cm ist das Farbzuordnungsmodul von Matplotlib. Es bietet eine Reihe von Farbschemata, einschließlich Einzelton, segmentierter Farbgebung und kontinuierlicher Farbverläufe, die den Anforderungen der Datenvisualisierung besser gerecht werden können. set_color：设置连接线的颜色；

• set_linewidth：设置连接线的线宽；

• set_linestyle：设置连接线的线型。

cm是Matplotlib的颜色映射模块，它提供了一系列的颜色方案，包括了单色调，分段调色和连续渐变调色等多种颜色方案，能够更好的满足数据可视化中的需求。

二、准备数据

# 大饼图数据
labels = ['301', '302', '303', '304', '305', '307', '308', '306']
size = [219324, 94739, 75146, 71831, 54051, 21458, 9990, 50843]
# 大饼图分裂距离
explode = (0, 0, 0, 0, 0, 0, 0, 0.1)
# 小饼图数据
labels2 = ['402', '407']
size2 = [12255, 207069]
width = 0.2

这段代码用于定义大饼图和小饼图的数据，并设置大饼图的分裂距离和小饼图的宽度。

具体解释如下：

• labels：定义大饼图每个分裂块的标签，即分别表示哪个区域。

• size：定义大饼图每个分裂块的大小，即表示每个区域的数量或占比。

• explode：定义大饼图每个分裂块距离饼心的距离，即分裂块是否需要弹出，这里设置为不弹出。

• labels2：定义小饼图每个分裂块的标签，即分别表示哪个区域。

• size2：定义小饼图每个分裂块的大小，即表示每个区域的数量或占比。

• width：定义小饼图的宽度，这里设置为0.2。

三、绘制双饼图

3.1 创建画布和子图对象

fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

这部分代码创建了一个大小为 (9, 5) 的画布 fig，并在该画布上添加了两个子图 ax1 和 ax2。

其中，fig.add_subplot(121) 表示将画布分为 1 行 2 列的子图，选择第 1 个子图（即左边的子图）；fig.add_subplot(122)

2. Daten vorbereiten

ax1.pie(size,
        autopct='%1.1f%%',
        startangle=30,
        labels=labels,
        colors=cm.Blues(range(10, 300, 50)),
        explode=explode)

Dieser Code wird verwendet, um die Daten des großen Kreisdiagramms und des kleinen Kreisdiagramms zu definieren und den Teilungsabstand des großen Kreisdiagramms und die Breite des kleinen Kreisdiagramms festzulegen.

Die spezifische Erklärung lautet wie folgt:

• Beschriftungen: Definieren Sie die Beschriftungen jedes geteilten Blocks des Kreisdiagramms, d. h. welchen Bereich jeder darstellt.

• Größe: Definieren Sie die Größe jedes geteilten Blocks des Kreisdiagramms, also die Anzahl oder den Anteil jedes Bereichs.

• explodieren: Definieren Sie den Abstand zwischen jedem geteilten Block des großen Kreisdiagramms und der Mitte des Kreises, d. h., ob der geteilte Block angezeigt werden soll. Hier wird festgelegt, dass er nicht angezeigt wird.

• labels2: Definieren Sie die Beschriftung jedes geteilten Blocks des kleinen Kreisdiagramms, also den Bereich, den er darstellt.

• Größe2: Definieren Sie die Größe jedes geteilten Blocks des kleinen Kreisdiagramms, d. h. die Anzahl oder den Anteil jedes Bereichs.

• Breite: Definieren Sie die Breite des Kreisdiagramms, hier auf 0,2 eingestellt.

3. Zeichnen Sie ein Doppelkreisdiagramm

3.1 Erstellen Sie Leinwand- und Unterfigurenobjekte

ax2.pie(size2,
        autopct='%1.1f%%',
        startangle=90,
        labels=labels2,
        colors=cm.Blues(range(10, 300, 50)),
        radius=0.5,
        shadow=False)

Dieser Teil des Codes erstellt eine Leinwandfigur mit einer Größe von (9, 5) und fügt zwei Unterfiguren ax1 und ax2 hinzu.

• Unter anderem bedeutet fig.add_subplot(121), die Leinwand in Unterhandlungen mit 1 Zeile und 2 Spalten zu unterteilen und die erste Unterhandlung (d. h. die Unterhandlung auf der linken Seite) auszuwählen; add_subplot( 122) bedeutet die Auswahl des zweiten Unterbilds (d. h. des Unterbilds rechts). Die Nummerierungsregel des Untergraphen ähnelt dem Array-Index. Die Zeilennummer erhöht sich von 1 nach unten und die Spaltennummer erhöht sich von 1 nach links. Beispielsweise stellt (1, 1) den Untergraphen des ersten dar Zeile und erste Spalte, ( 1, 2) stellt den Untergraphen der ersten Zeile und der zweiten Spalte dar. Hier repräsentieren 121 und 122 den ersten bzw. zweiten Untergraphen der ersten Zeile.
  3.2 Zeichnen eines großen Kreisdiagramms

theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)

• Dieser Code wird verwendet, um ein Kreisdiagramm im ersten Untergraphen (ax1) zu zeichnen. Die Bedeutung der spezifischen Parameter ist wie folgt:

• Größe: Kreisdiagrammdaten, die die Größe jedes Kreisdiagrammblocks angeben.

• autopct: Das Datenbeschriftungsformat des Kreisdiagrammblocks „%1.1f%%“ bedeutet, dass eine Dezimalstelle beibehalten und ein Prozentzeichen hinzugefügt wird.

• Startwinkel: Der Startwinkel des Kreisdiagramms, 30 Grad ist der Startpunkt, im Uhrzeigersinn drehen.

• Beschriftungen: Beschriftungen von Kreisdiagrammblöcken, entsprechend der Größe.

• Farben: Die Farben der Kreisdiagrammblöcke, wobei die Funktion cm.Blues() zum Generieren einer Farbliste verwendet wird.
  🎜🎜explodieren: Der Teilungsabstand des Kreisdiagrammblocks, der angibt, ob er von der Mitte des Kreisdiagramms getrennt ist. Beispielsweise bedeutet (0, 0, 0, 0, 0, 0, 0, 0,1), dass das letzte Kreisstück 0,1 Radien von der Mitte entfernt ist. 🎜🎜🎜🎜Diese Parameter und die anderer Kreisdiagramme können nach Bedarf angepasst werden, um den gewünschten Effekt zu erzielen. 🎜🎜3.3 Zeichnen eines Kreisdiagramms🎜

  x = r * np.cos(np.pi / 180 * theta1) + center[0]
  y = np.sin(np.pi / 180 * theta1) + center[1]
  con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                         xyB=(x, y),
                         coordsA='data',
                         coordsB='data',
                         axesA=ax2, axesB=ax1)

  🎜Dieser Code wird zum Zeichnen des zweiten Kreisdiagramms verwendet. Die spezifischen Parameterbedeutungen sind wie folgt: 🎜🎜🎜🎜size2: die Daten des kleinen Kreisdiagramms, also [12255, 207069]; 🎜🎜🎜🎜autopct: die Datenbezeichnung des formatierten keilförmigen Blocks ‘ %1.1f%% bedeutet reserviert Eine Dezimalstelle, gefolgt von einem Prozentzeichen 🎜🎜🎜🎜Startwinkel: der Startwinkel des Kreisdiagramms, ausgedrückt in Grad, hier auf 90 Grad eingestellt, also ausgehend von der Vertikalen Richtung; 🎜🎜🎜🎜labels2: Die Beschriftung des kleinen Kreisdiagramms, nämlich [‘402’, ‘407’]; 🎜🎜🎜🎜colors: Geben Sie die Farbe an, hier wird die cm.Blues-Funktion verwendet, um eine zu generieren Satz blauer Serienfarben; 🎜🎜🎜🎜radius: kleiner Kreis Der Radius des Bildes wird hier auf 0,5 eingestellt. 🎜🎜🎜🎜Shadow: Gibt an, ob ein Schatten hinzugefügt werden soll. 🎜

在这段代码中，我们创建了一个名为 ax2 的子区域对象，并使用 pie 方法绘制了一个小饼图，将 size2 中的数据作为输入数据。其他参数指定了锲形块的格式、颜色、标签等属性，进一步定制了图形的样式。

3.4 连接线1，连接大饼图的上边缘和小饼图的饼块

theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)

这部分代码是用来计算连接两个饼图的连接线的起点和终点位置，并创建一个 ConnectionPatch 对象用于绘制连接线。

• theta1 和 theta2 分别表示饼图上最后一个扇形的起始角度和终止角度。

• center 表示饼图中最后一个扇形的中心点位置。

• r 表示饼图的半径。

• x 和 y 表示连接线的终点坐标，其中 x 通过利用三角函数计算出来。

接下来，ConnectionPatch 的参数解释：

• xyA 表示连接线的起点位置，这里设为 (0, 0.5) 表示在小饼图上以它的左边中间位置为起点。

• xyB 表示连接线的终点位置，这里为 (x, y) 表示在大饼图上以计算得到的 x 和 y 为终点位置。

• coordsA 和 coordsB 表示起点和终点所在的坐标系，这里分别为小饼图和大饼图的坐标系。

• axesA 和 axesB 分别表示起点和终点所在的子图对象，这里分别为小饼图和大饼图的子图对象，即 ax2 和 ax1。

3.5 连接线2，连接大饼图的下边缘和小饼图的饼块

x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = np.sin(np.pi / 180 * theta1) + center[1]
con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                       xyB=(x, y),
                       coordsA='data',
                       coordsB='data',
                       axesA=ax2, axesB=ax1)

这段代码用于创建连接线的第二个对象con2。具体解释如下：

• x 和 y 分别代表了连接线从小饼图中(-0.1,-0.49)这个点出发，到大饼图中theta1角度对应的点的终点坐标。其中，theta1是通过访问ax1.patches[-1].theta1获得的。

• coordsA 和 coordsB 表示终点和起点坐标的坐标系类型。这里都是 ‘data’ 表示使用数据坐标系，即默认的 x 和 y 坐标值。

• axesA 和 axesB 表示终点和起点所在的子图对象。其中，axesA 为小饼图，axesB 为大饼图。

• 这里使用ConnectionPatch函数创建连接线对象。

3.6 添加连接线

for con in [con1, con2]:
    con.set_color('gray')
    ax2.add_artist(con)
    con.set_linewidth(1)

这段代码用于设置连接线的颜色和粗细，并将连接线添加到小饼图的坐标系上。具体来说，循环遍历连接线对象列表 [con1, con2]，并依次对每个连接线进行以下操作：

• 调用 set_color() 方法设置连接线的颜色为灰色。

• 调用 ax2.add_artist() 方法将连接线添加到小饼图的坐标系上。

• 调用 set_linewidth() 方法设置连接线的宽度为 1。

3.7 调整子图布局

fig.subplots_adjust(wspace=0)
plt.show()

这行代码调整了子图之间的水平间距，将间距设置为0，即将子图紧密排列。wspace参数表示子图之间的宽度间距。具体来说，这行代码将第一个子图和第二个子图之间的间距设置为0，使它们之间没有空隙。

四、源代码

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import ConnectionPatch
from matplotlib import cm
# 大饼图数据
labels = ['301', '302', '303', '304', '305', '307', '308', '306']
size = [219324, 94739, 75146, 71831, 54051, 21458, 9990, 50843]
# 大饼图分裂距离
explode = (0, 0, 0, 0, 0, 0, 0, 0.1)
# 小饼图数据
labels2 = ['402', '407']
size2 = [12255, 207069]
width = 0.2
# 创建画布和子图对象
fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
# 绘制大饼图
ax1.pie(size,
        autopct='%1.1f%%',
        startangle=30,
        labels=labels,
        colors=cm.Blues(range(10, 300, 50)),
        explode=explode)
# 绘制小饼图
ax2.pie(size2,
        autopct='%1.1f%%',
        startangle=90,
        labels=labels2,
        colors=cm.Blues(range(10, 300, 50)),
        radius=0.5,
        shadow=False)
# 连接线1，连接大饼图的上边缘和小饼图的饼块
theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)
# 连接线2，连接大饼图的下边缘和小饼图的饼块
x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = np.sin(np.pi / 180 * theta1) + center[1]
con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                       xyB=(x, y),
                       coordsA='data',
                       coordsB='data',
                       axesA=ax2, axesB=ax1)
# 添加连接线
for con in [con1, con2]:
    con.set_color('gray')
    ax2.add_artist(con)
    con.set_linewidth(1)
# 调整子图布局
fig.subplots_adjust(wspace=0)
# 显示图像
plt.show()

可视化结果为：

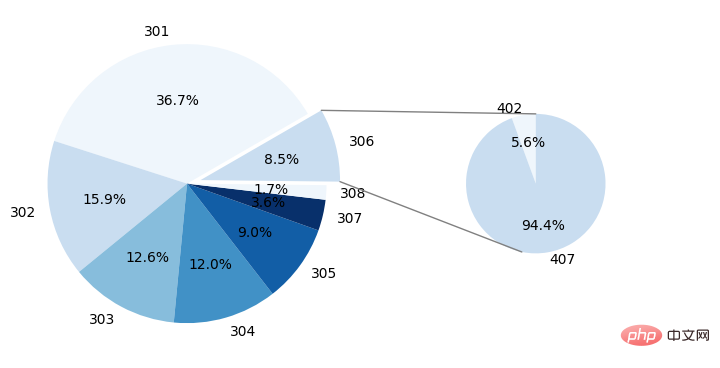
Das obige ist der detaillierte Inhalt vonSo zeichnen Sie in Python ein Doppelkreisdiagramm mit Verbindungslinien. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!