Verwendung von Python zur Implementierung der Punktwolken-Bodenerkennung

1. Computer-Vision-Koordinatensystem

Bevor Sie beginnen, ist es wichtig, das traditionelle Koordinatensystem in der Computer-Vision zu verstehen. Es folgen Open3D und der Microsoft Kinect-Sensor. Beim Computer Vision werden Bilder durch ein separates 2D-Koordinatensystem dargestellt, wobei die x-Achse von links nach rechts und die y-Achse nach oben und unten zeigt. Bei einer Kamera liegt der Ursprung des 3D-Koordinatensystems im Fokus der Kamera, wobei die x-Achse nach rechts, die y-Achse nach unten und die z-Achse nach vorne zeigt.

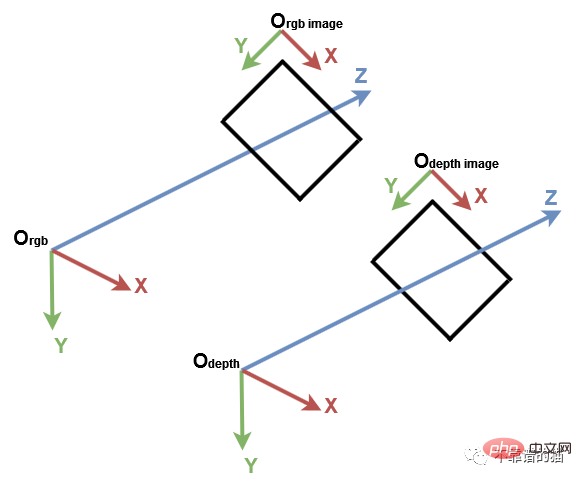
Computer Vision-Koordinatensystem

Wir importieren zunächst die erforderliche Python-Bibliothek:

import numpy as np
import open3d as o3d

Zum besseren Verständnis importieren wir Punktwolken aus PLY-Dateien, erstellen Standard-3D-Koordinatensysteme mit Open3D und zeigen sie an:

# Read point cloud:
pcd = o3d.io.read_point_cloud("data/depth_2_pcd.ply")
# Create a 3D coordinate system:
origin = o3d.geometry.TriangleMesh.create_coordinate_frame(size=0.5)
# geometries to draw:
geometries = [pcd, origin]
# Visualize:
o3d.visualization.draw_geometries(geometries)

Punktwolke mit dem Ursprung des Koordinatensystems angezeigt

Der blaue Pfeil ist die Z-Achse, der rote Pfeil ist die X-Achse und der grüne Pfeil ist die Y-Achse. Sie können sehen, dass die Punktwolke im selben Koordinatensystem wie das Open3D-Koordinatensystem dargestellt wird. Lassen Sie uns nun die Punkte mit den minimalen und maximalen Werten jeder Achse ermitteln:

# Get max and min points of each axis x, y and z:
x_max = max(pcd.points, key=lambda x: x[0])
y_max = max(pcd.points, key=lambda x: x[1])
z_max = max(pcd.points, key=lambda x: x[2])
x_min = min(pcd.points, key=lambda x: x[0])
y_min = min(pcd.points, key=lambda x: x[1])
z_min = min(pcd.points, key=lambda x: x[2])

Wir können sie ausdrucken, aber zur besseren Visualisierung erstellen wir an jeder Punktposition eine Kugel. Standardmäßig erstellt Open3D 3D-Geometrien an der Ursprungsposition:

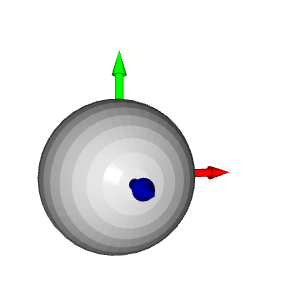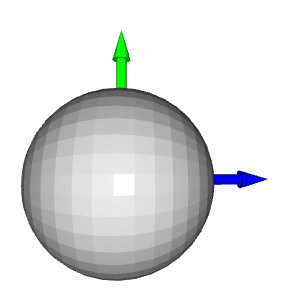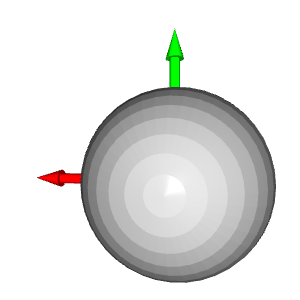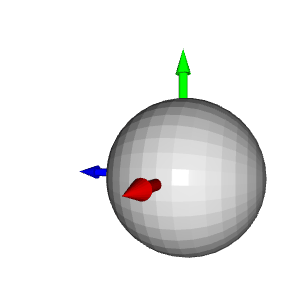
Um die Kugel an eine bestimmte Position zu bewegen, ist eine Translationstransformation erforderlich. Im folgenden Beispiel wird die Kugel durch den Vektor [1,1,1] übersetzt:

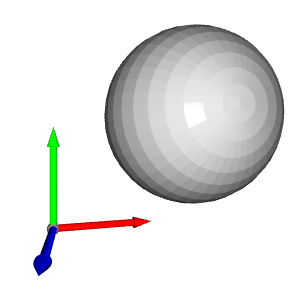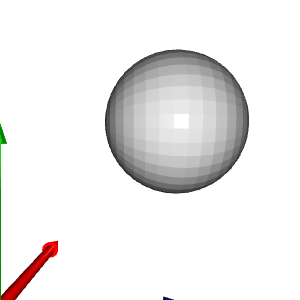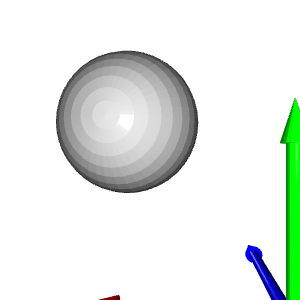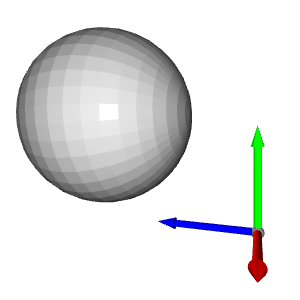
Kehren wir zu unserem Beispiel zurück und weisen jeder Kugel eine Farbe zu. Für jede Position erstellen wir eine Kugel und verschieben sie in diese Position. Dann weisen wir die richtige Farbe zu und fügen sie schließlich der Anzeige hinzu.

# Colors:
RED = [1., 0., 0.]
GREEN = [0., 1., 0.]
BLUE = [0., 0., 1.]
YELLOW = [1., 1., 0.]
MAGENTA = [1., 0., 1.]
CYAN = [0., 1., 1.]


positions = [x_max, y_max, z_max, x_min, y_min, z_min]
colors = [RED, GREEN, BLUE, MAGENTA, YELLOW, CYAN]
for i in range(len(positions)):
 # Create a sphere mesh:
 sphere = o3d.geometry.TriangleMesh.create_sphere(radius=0.05)
 # move to the point position:
 sphere.translate(np.asarray(positions[i]))
 # add color:
 sphere.paint_uniform_color(np.asarray(colors[i]))
 # compute normals for vertices or faces:
 sphere.compute_vertex_normals()
 # add to geometry list to display later:
 geometries.append(sphere)


# Display:
o3d.visualization.draw_geometries(geometries)

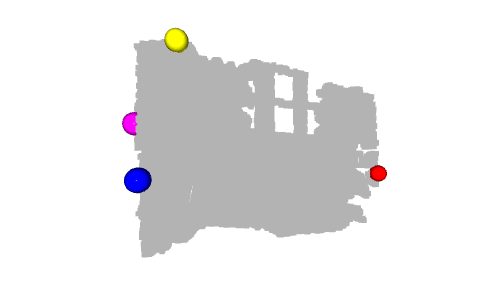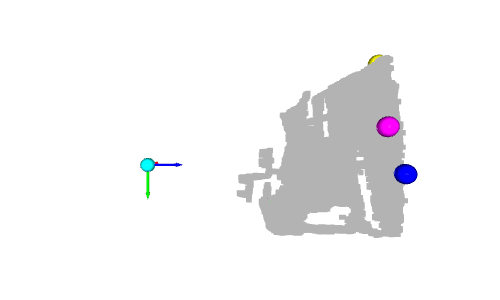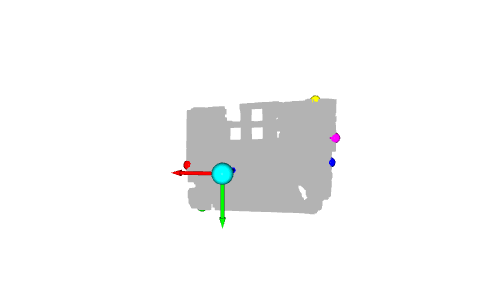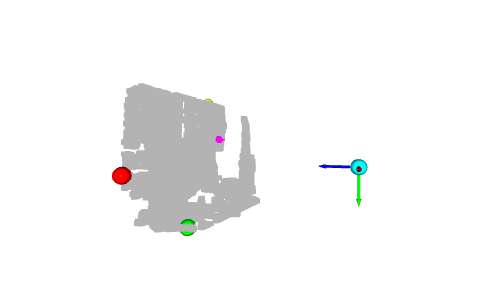
Eigentlich stellt die y-Achse die Höhe des Punktes dar: In der realen Welt ist der höchste Ball der gelbe Ball und der niedrigste Ball der grüne Ball. Da die y-Achse jedoch nach unten zeigt, hat die gelbe Kugel den kleinsten Wert und die grüne Kugel den größten Wert.

Eine weitere interessante Kugel ist die cyanfarbene Kugel am Ursprung. Wie wir im vorherigen Tutorial erwähnt haben, sind Pixel mit einem Tiefenwert von 0 Rauschpunkte, daher ist der Punkt am Ursprung der aus diesen Rauschpixeln berechnete Punkt (wenn z=0, dann ist x=0 und y=0).

2. Bodenerkennung

Nachdem wir nun einige wichtige Punkte gezeigt haben, wie wäre es mit der Bodenerkennung? Im vorherigen Beispiel befindet sich die grüne Kugel auf dem Boden. Genauer gesagt entspricht sein Mittelpunkt dem höchsten Punkt entlang der y-Achse, der ein Bodenpunkt ist. Angenommen, wir ändern zur Bodenerkennung die Farbe aller Punkte mit y_max in Grün.

Wenn Sie die Punktwolke anzeigen, werden Sie feststellen, dass nicht alle Bodenpunkte grün sind. Tatsächlich ist nur ein Punkt grün, der dem Mittelpunkt der vorherigen grünen Kugel entspricht. Dies ist auf die Genauigkeit und das Rauschen der Tiefenkamera zurückzuführen.

Um diese Einschränkung zu überwinden, müssen wir einen Schwellenwert hinzufügen, sodass Punkte mit den Y-Koordinaten [y_max-threshold, y_max] als Bodenpunkte betrachtet werden. Dazu prüfen wir nach Erhalt von y_max, ob die y-Koordinate jedes Punkts innerhalb des Intervalls liegt und setzen dann seine Farbe auf Grün. Abschließend werden die Farbattribute der Punktwolke aktualisiert und die Ergebnisse angezeigt.

# Define a threshold:
THRESHOLD = 0.075


# Get the max value along the y-axis:
y_max = max(pcd.points, key=lambda x: x[1])[1]


# Get the original points color to be updated:
pcd_colors = np.asarray(pcd.colors)


# Number of points:
n_points = pcd_colors.shape[0]


# update color:
for i in range(n_points):
# if the current point is aground point:
if pcd.points[i][1] >= y_max - THRESHOLD:
pcd_colors[i] = GREEN# color it green


pcd.colors = o3d.utility.Vector3dVector(pcd_colors)


# Display:
o3d.visualization.draw_geometries([pcd, origin])

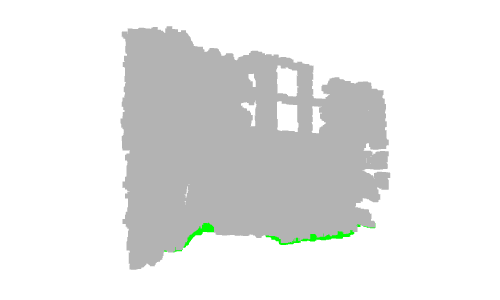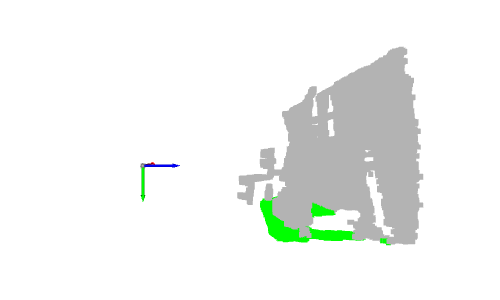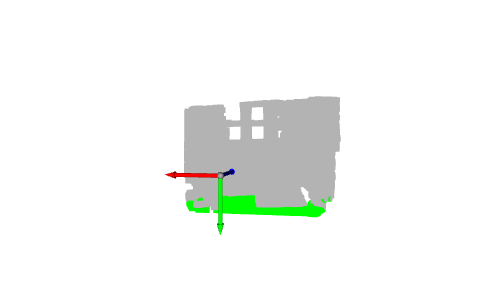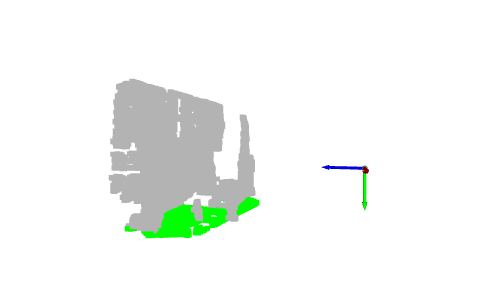
In diesem Fall färben wir nur die Punkte, die den Boden darstellen, grün. In realen Anwendungen wird der Boden entnommen, um begehbare Bereiche zu definieren, beispielsweise für Roboter oder sehbehinderte Systeme, oder um Objekte darauf zu platzieren, beispielsweise Innenarchitektursysteme. Es kann auch entfernt werden, sodass die verbleibenden Punkte segmentiert oder klassifiziert werden können, wie bei Szenenverständnis- und Objekterkennungssystemen.

3. Organisierte Punktwolke

Wir wissen, dass eine Punktwolke als eine Menge von 3D-Punkten definiert ist. Eine Menge ist eine ungeordnete Struktur, daher wird die durch die Menge dargestellte Punktwolke als unorganisierte Punktwolke bezeichnet. Ähnlich einer RGB-Matrix ist eine organisierte Punktwolke eine 2D-Matrix mit drei Kanälen, die die x-, y- und z-Koordinaten der Punkte darstellen. Die Matrixstruktur stellt die Beziehung zwischen benachbarten Punkten bereit und reduziert dadurch die zeitliche Komplexität einiger Algorithmen, beispielsweise des Algorithmus für den nächsten Nachbarn.

Zum Beispiel schreiben wir eine Forschungsarbeit und möchten die Ergebnisse unseres Erkennungsalgorithmus in Diagrammform darstellen. Wir können entweder einen Screenshot der Punktwolke machen oder die Ergebnisse auf einem Tiefenbild anzeigen, wie unten gezeigt. Meiner Meinung nach ist die zweite Option die beste. In diesem Fall ist eine organisierte Punktwolke erforderlich, um die Positionen der Tiefenpixel zu speichern.

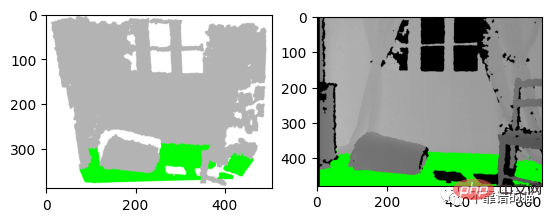
左：3D 可视化的屏幕截图 右：深度图像的结果

让我们从之前的深度图像创建一个有组织的点云。我们首先导入相机参数。我们还导入深度图像并将其转换为3通道灰度图像，以便我们可以将地面像素设置为绿色：

import imageio.v3 as iio
import numpy as np
import matplotlib.pyplot as plt


# Camera parameters:
FX_DEPTH = 5.8262448167737955e+02
FY_DEPTH = 5.8269103270988637e+02
CX_DEPTH = 3.1304475870804731e+02
CY_DEPTH = 2.3844389626620386e+02


# Read depth image:
depth_image = iio.imread('../data/depth_2.png')
# Compute the grayscale image:
depth_grayscale = np.array(256 * depth_image / 0x0fff, dtype=np.uint8)
# Convert a grayscale image to a 3-channel image:
depth_grayscale = np.stack((depth_grayscale,) * 3, axis=-1)

要计算一个有组织的点云，我们使用与上一篇教程相同的方法（Python：基于 RGB-D 图像的点云计算）。我们没有将深度图像扁平化，而是将jj和ii重塑为与深度图像相同的形状，如下所示:

# get depth image resolution:
height, width = depth_image.shape
# compute indices and reshape it to have the same shape as the depth image:
jj = np.tile(range(width), height).reshape((height, width))
ii = np.repeat(range(height), width).reshape((height, width))
# Compute constants:
xx = (jj - CX_DEPTH) / FX_DEPTH
yy = (ii - CY_DEPTH) / FY_DEPTH
# compute organised point cloud:
organized_pcd = np.dstack((xx * depth_image, yy * depth_image, depth_image))

如果你打印出创建的点云的形状，你可以看到它是一个有3个通道的矩阵(480,640,3)。如果你觉得这个代码很难理解，请回到之前的教程（Python：基于 RGB-D 图像的点云计算）。

类似地，我们像上面那样检测地面，但不是更新点的颜色并显示点云，而是更新灰度图像的像素并显示它:

# Ground_detection:
THRESHOLD = 0.075 * 1000# Define a threshold
y_max = max(organized_pcd.reshape((height * width, 3)), key=lambda x: x[1])[
1]# Get the max value along the y-axis


# Set the ground pixels to green:
for i in range(height):
for j in range(width):
if organized_pcd[i][j][1] >= y_max - THRESHOLD:
depth_grayscale[i][j] = [0, 255, 0]# Update the depth image


# Display depth_grayscale:
plt.imshow(depth_grayscale)
plt.show()

4.结论

在本教程中，为了熟悉点云，我们引入了默认坐标系统，并实现了一个简单的地面检测算法。事实上，地面检测在某些应用(如导航)中是一项重要的任务，文献中已经提出了几种算法。实现算法简单;它认为最低点是地面。然而，它的限制是，深度相机必须与地面平行，这是大多数现实应用的情况不是这样的。

Das obige ist der detaillierte Inhalt vonVerwendung von Python zur Implementierung der Punktwolken-Bodenerkennung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!