Heim >Java >javaLernprogramm >Welche gängigen Algorithmen werden in der Java-Entwicklung häufig verwendet?
Welche gängigen Algorithmen werden in der Java-Entwicklung häufig verwendet?
- 王林nach vorne
- 2023-05-09 10:04:151648Durchsuche
Gieriger Algorithmus
Klassische Anwendungen: wie Huffman Coding, Prim- und Kruskal-Minimum-Spanning-Tree-Algorithmen und Dijkstra-Single-Source-Shortest-Path-Algorithmus.
Die Schritte des Greedy-Algorithmus zur Lösung des Problems
Der erste Schritt: Wenn wir ein solches Problem sehen, müssen wir zunächst an den gierigen Algorithmus denken: Für einen Datensatz definieren wir den Grenzwert und den erwarteten Wert und hoffen, einen auszuwählen wenige Daten daraus. Der Erwartungswert ist maximal, wenn der Grenzwert erreicht wird.
Analog zum Beispiel eben gilt: Der Grenzwert darf 100 kg nicht überschreiten und der Erwartungswert ist der Gesamtwert des Artikels. Dieser Datensatz umfasst 5 Bohnensorten. Wir wählen einen Teil davon aus, der nicht mehr als 100 kg wiegt und den höchsten Gesamtwert hat.
Im zweiten Schritt versuchen wir herauszufinden, ob dieses Problem mit einem Greedy-Algorithmus gelöst werden kann: Wählen Sie jedes Mal die Daten aus, die unter der aktuellen Situation am meisten zum erwarteten Wert beitragen Beitrag zum Grenzwert.
Analog zum Beispiel gerade wählen wir unter den restlichen Bohnen immer diejenige mit dem höchsten Stückpreis aus, also mit dem gleichen Gewicht , diejenige, die dazu beiträgt die wertvollsten Bohnen.
Im dritten Schritt geben wir einige Beispiele, um zu sehen, ob die vom Greedy-Algorithmus erzeugten Ergebnisse optimal sind. In den meisten Fällen genügt es, ein paar Beispiele zu nennen, um dies zu überprüfen. Der strenge Beweis der Korrektheit des Greedy-Algorithmus ist sehr kompliziert und erfordert viel mathematisches Denken.
Der Hauptgrund, warum der Greedy-Algorithmus nicht funktioniert, ist, dass die vorherigen Entscheidungen die nachfolgenden Entscheidungen beeinflussen.
Praktische Analyse des Greedy-Algorithmus
1. Süßigkeiten teilen
Wir haben m Süßigkeiten und n Kinder. Wir wollen nun Süßigkeiten an diese Kinder verteilen, aber es gibt weniger Süßigkeiten und mehr Kinder (m Wir können dieses Problem abstrahieren, indem wir aus n Kindern einen Teil der Kinder auswählen, um Süßigkeiten zu verteilen, sodass die Anzahl der zufriedenen Kinder (erwarteter Wert) am größten ist. Der Grenzwert dieses Problems ist die Anzahl der Bonbons m.
Jedes Mal finden wir unter den verbleibenden Kindern dasjenige mit der geringsten Nachfrage nach Bonbongröße und geben ihm dann unter den verbleibenden Bonbons das kleinste Bonbon, das ihn befriedigen kann. Der auf diese Weise erhaltene Verteilungsplan ist, Das heißt, der Plan, der die meisten Kinder zufriedenstellt.
2. Münzwechsel
Dieses Problem tritt in unserem täglichen Leben häufiger auf. Angenommen, wir haben Banknoten zu 1 Yuan, 2 Yuan, 5 Yuan, 10 Yuan, 20 Yuan, 50 Yuan und 100 Yuan. Ihre Nummern sind c1, c2, c5, c10, c20, c50 und c100. Mit diesem Geld müssen wir nun K Yuan bezahlen. Wie viele Banknoten müssen wir mindestens verwenden?
Im Leben müssen wir zuerst mit dem Betrag mit dem größten Nennwert bezahlen. Wenn dies nicht ausreicht, verwenden wir weiterhin einen kleineren Nennwert usw. und verwenden schließlich 1 Yuan den Rest ausmachen. Wenn wir den gleichen erwarteten Wert (Anzahl der Banknoten) beisteuern, hoffen wir, mehr beizutragen, sodass die Anzahl der Banknoten reduziert werden kann. Dies ist die Lösung eines gierigen Algorithmus.
3. Intervallabdeckung
Angenommen, wir haben n Intervalle. Die Start- und Endpunkte des Intervalls sind [l1, r1], [l2, r2], [l3, r3], ..., [ln, rn]. . Wir wählen einen Teil der Intervalle aus diesen n Intervallen aus. Dieser Teil des Intervalls erfüllt, dass sich jedes Intervallpaar nicht schneidet (die Endpunkte gelten nicht als Schnittpunkte).
Diese Verarbeitungsidee wird in vielen Problemen mit gierigen Algorithmen verwendet, z. B. bei der Aufgabenplanung, der Lehrerplanung usw.
Die Lösung für dieses Problem lautet wie folgt: Wir gehen davon aus, dass der Endpunkt ganz links dieser n Intervalle lmin und der Endpunkt ganz rechts rmax ist. Dieses Problem entspricht der Auswahl mehrerer disjunkter Intervalle und der Abdeckung von [lmin, rmax] von links nach rechts. Wir sortieren diese n Intervalle in der Reihenfolge von kleinen zu großen Startendpunkten.
Bei jeder Auswahl stimmt der linke Endpunkt nicht mit dem zuvor abgedeckten Intervall überein und der rechte Endpunkt ist so klein wie möglich, sodass das verbleibende nicht abgedeckte Intervall so groß wie möglich gemacht werden kann Intervalle können platziert werden. Dies ist eigentlich eine gierige Auswahlmethode.
Wie verwende ich den Greedy-Algorithmus, um die Huffman-Codierung zu implementieren?
Die Huffman-Codierung verwendet diese Codierungsmethode mit ungleicher Länge zum Codieren von Zeichen. Es ist erforderlich, dass es zwischen den Kodierungen der einzelnen Zeichen keine Situation gibt, in der eine Kodierung das Präfix einer anderen Kodierung ist. Verwenden Sie etwas kürzere Codes für Zeichen, die häufiger vorkommen; verwenden Sie etwas längere Codes für Zeichen, die weniger häufig vorkommen.
Angenommen, ich habe eine Datei mit 1000 Zeichen. Es werden insgesamt 8000 Bit benötigt, um diese 1000 Zeichen zu speichern.
Angenommen, wir stellen durch statistische Analyse fest, dass diese 1000 Zeichen nur 6 verschiedene Zeichen enthalten, vorausgesetzt, es handelt sich um a, b, c, d, e, f. 3 Binärbits (Bits) können 8 verschiedene Zeichen darstellen. Um den Speicherplatz zu minimieren, verwenden wir daher 3 Binärbits zur Darstellung jedes Zeichens. Dann sind zum Speichern dieser 1000 Zeichen nur 3000 Bit erforderlich, was gegenüber der ursprünglichen Speichermethode viel Platz spart. Gibt es jedoch eine platzsparendere Aufbewahrungsmethode?
a(000), b(001), c(010), d(011), e(100), f(101)
Huffman-Codierung ist eine sehr effektive Codierungsmethode und wird häufig bei der Datenkomprimierung verwendet. Ihre Komprimierungsrate liegt normalerweise zwischen 20 % und 90 %.
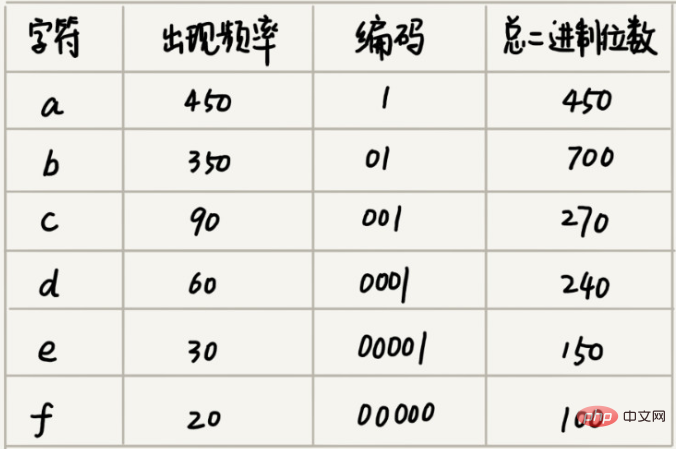
Die Huffman-Codierung untersucht nicht nur, wie viele verschiedene Zeichen im Text vorhanden sind, sondern untersucht auch die Häufigkeit des Auftretens jedes Zeichens und wählt basierend auf der Häufigkeit Codes unterschiedlicher Länge aus. Bei der Huffman-Codierung wird versucht, diese Codierungsmethode mit ungleicher Länge zu nutzen, um die Komprimierungseffizienz weiter zu erhöhen. Wie wähle ich unterschiedliche Längencodes für Zeichen mit unterschiedlichen Häufigkeiten aus? Basierend auf dem gierigen Denken können wir für Zeichen, die häufiger vorkommen, etwas kürzere Codes verwenden; für Zeichen, die weniger häufig vorkommen, können wir etwas längere Codes verwenden.
Die Codes sind nicht gleich lang. Wie liest man sie und analysiert sie?
Für die Codierung gleicher Länge ist die Dekomprimierung für uns sehr einfach. Im Beispiel gerade verwenden wir beispielsweise 3 Bits, um ein Zeichen darzustellen. Beim Dekomprimieren lesen wir jeweils 3-stellige Binärcodes aus dem Text und übersetzen sie in entsprechende Zeichen. Allerdings sind Huffman-Codes nicht gleich lang. Sollten jedes Mal 1 Bit oder 2 Bits, 3 Bits usw. zur Dekomprimierung gelesen werden? Dieses Problem macht die Dekomprimierung der Huffman-Codierung schwieriger. Um Mehrdeutigkeiten während des Dekomprimierungsprozesses zu vermeiden, erfordert die Huffman-Kodierung, dass es zwischen den Kodierungen jedes Zeichens keine Situation gibt, in der eine Kodierung das Präfix einer anderen Kodierung ist.
Angenommen, die Häufigkeit dieser 6 Zeichen von hoch nach niedrig ist a, b, c, d, e, f. Wir kodieren sie auf diese Weise. Beim Dekomprimieren lesen wir jedes Mal eine möglichst lange dekomprimierbare Binärzeichenfolge, damit keine Mehrdeutigkeit entsteht. Nach dieser Kodierung und Komprimierung benötigen diese 1000 Zeichen nur noch 2100 Bit.
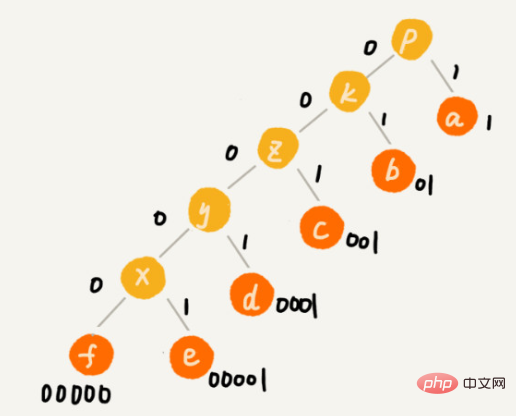
Obwohl die Idee der Huffman-Codierung nicht schwer zu verstehen ist, Wie codiert man verschiedene Zeichen mit unterschiedlichen Längen entsprechend der Häufigkeit des Auftretens von Zeichen?
Verwenden Sie einen großen Stapel, um Zeichen entsprechend der Häufigkeit zu platzieren.
Teile-und-herrsche-Algorithmus
Die Kernidee des Divide-and-Conquer-Algorithmus besteht eigentlich aus vier Worten: Divide and Conquer, also das ursprüngliche Problem in n kleinere Unterprobleme mit einer ähnlichen Struktur wie das ursprüngliche Problem aufteilen. Lösen Sie diese Teilprobleme rekursiv und kombinieren Sie dann ihre Ergebnisse, um eine Lösung für das ursprüngliche Problem zu erhalten.
Der Divide-and-Conquer-Algorithmus ist eine Idee zur Lösung von Problemen, und Rekursion ist eine Programmiertechnik. Tatsächlich eignen sich Divide-and-Conquer-Algorithmen im Allgemeinen besser für die Implementierung mithilfe von Rekursion. Bei der rekursiven Implementierung des Divide-and-Conquer-Algorithmus umfasst jede Rekursionsebene die folgenden drei Operationen:
Zerlegung: Zerlegen Sie das ursprüngliche Problem in eine Reihe von Unterproblemen. Wenn die Unterprobleme klein genug sind, lösen Sie sie direkt. 🎜🎜# Unterprobleme können mit dem ursprünglichen Problem zusammengeführt werden, die Komplexität dieser Zusammenführungsoperation darf jedoch nicht zu hoch sein, da sonst die Gesamtkomplexität des Algorithmus nicht verringert wird. Wie programmiert man, um die Anzahl der geordneten Paare oder die Anzahl der umgekehrten Paare eines Datensatzes zu ermitteln?
Vergleichen Sie jede Zahl mit der Zahl danach, um zu sehen, wie viele kleiner sind als sie. Wir notieren die Anzahl der kleineren Zahlen als k. Auf diese Weise summieren wir nach der Untersuchung jeder Zahl die k-Werte, die jeder Zahl entsprechen. Die resultierende Endsumme ist die Anzahl der Paare in umgekehrter Reihenfolge. Die zeitliche Komplexität dieser Operation beträgt jedoch O(n^2).
Wir können das Array in zwei Hälften teilen, A1 und A2, die Anzahl der Paare in umgekehrter Reihenfolge K1 und K2 von A1 bzw. A2 berechnen und dann die Anzahl der Paare in umgekehrter Reihenfolge K3 zwischen A1 und A2 berechnen. Dann ist die Anzahl der Paare umgekehrter Reihenfolge in Array A gleich K1+K2+K3. Mit Hilfe des Zusammenführungssortierungsalgorithmus
Müssen die 10-GB-Bestelldateien nach Menge sortiert werden?
Wir können die Bestellung zunächst scannen und die 10-GB-Datei basierend auf der Bestellmenge in mehrere Mengenbereiche aufteilen. Beispielsweise wird der Bestellbetrag zwischen 1 und 100 Yuan in einer kleinen Datei abgelegt, der Bestellbetrag zwischen 101 und 200 wird in einer anderen Datei abgelegt und so weiter. Auf diese Weise kann jede kleine Datei zum separaten Sortieren in den Speicher geladen werden. Anschließend werden diese geordneten kleinen Dateien zusammengeführt, um die endgültigen geordneten 10-GB-Bestelldaten zu erhalten.
Backtracking-Algorithmus
Anwendungsszenarien: Tiefensuche, Vergleich regulärer Ausdrücke, Syntaxanalyse in Kompilierungsprinzipien. Viele klassische mathematische Probleme können mit dem Backtracking-Algorithmus gelöst werden, wie z. B. Sudoku, Acht Damen, 0-1-Rucksack, Diagrammfärbung, Problem des Handlungsreisenden, Gesamtpermutation usw.
Die Verarbeitungsidee des Backtracking ähnelt in gewisser Weise der Aufzählungssuche. Wir zählen alle Lösungen auf und finden die Lösung, die unseren Erwartungen entspricht. Um regelmäßig alle Lösungsmöglichkeiten aufzuzählen und Auslassungen und Duplikate zu vermeiden, unterteilen wir den Problemlösungsprozess in mehrere Phasen. In jeder Phase stehen wir vor einer Weggabelung. Wenn wir feststellen, dass dieser Weg nicht funktioniert (nicht der erwarteten Lösung entspricht), kehren wir zur vorherigen Weggabelung zurück Wähle einen anderen Weg.
Acht-Damen-Problem
Wir haben ein 8x8-Schachbrett und möchten 8 Schachfiguren (Damen) darauf platzieren. Jede Schachfigur darf keine weitere Schachfigur in der Reihe, Spalte oder Diagonale haben.
1,0-1 Rucksack
Viele Szenarien können in dieses Problemmodell abstrahiert werden. Die klassische Lösung für dieses Problem ist die dynamische Programmierung, aber es gibt auch eine einfache, aber weniger effiziente Lösung, nämlich den Backtracking-Algorithmus, über den wir heute sprechen.
Wir haben einen Rucksack und das Gesamttraggewicht des Rucksacks beträgt Wkg. Jetzt haben wir n Elemente, von denen jedes ein anderes Gewicht hat und unteilbar ist. Wir wollen nun ein paar Gegenstände auswählen und in unseren Rucksack laden. Wie kann das Gesamtgewicht der Gegenstände in einem Rucksack maximiert werden, ohne das Gewicht zu überschreiten, das der Rucksack tragen kann?
Für jeden Gegenstand gibt es zwei Möglichkeiten: in den Rucksack stecken oder nicht in den Rucksack stecken. Für n Elemente gibt es 2^n Möglichkeiten, sie zu installieren. Entfernen Sie diejenigen mit einem Gesamtgewicht von mehr als Wkg und wählen Sie aus den verbleibenden Installationsmethoden dasjenige aus, dessen Gesamtgewicht Wkg am nächsten kommt. Wie können wir jedoch diese 2^n Arten des Vortäuschens ohne Wiederholung erschöpfend aufzählen?
Backtracking-Methode: Wir können die Elemente in der richtigen Reihenfolge anordnen, und das gesamte Problem wird in n Phasen zerlegt, und jede Phase entspricht der Auswahl eines Elements. Verarbeiten Sie zuerst das erste Element, entscheiden Sie, ob es geladen werden soll oder nicht, und verarbeiten Sie dann die restlichen Elemente rekursiv.
Dynamische Programmierung
Dynamische Programmierung eignet sich besser zur Lösung optimaler Probleme, z. B. zum Finden von Maximalwerten, Minimalwerten usw. Es kann die Zeitkomplexität erheblich reduzieren und die Effizienz der Codeausführung verbessern.
0-1 Rucksackproblem
Für eine Reihe unteilbarer Gegenstände mit unterschiedlichem Gewicht müssen wir einige auswählen, die wir in den Rucksack stecken möchten. Wie hoch ist das maximale Gesamtgewicht der Gegenstände im Rucksack?
Gedanken:
(1) Teilen Sie den gesamten Lösungsprozess in n Phasen auf, und jede Phase entscheidet darüber, ob ein Gegenstand in den Rucksack gelegt wird. Nachdem für jeden Gegenstand entschieden wurde (in den Rucksack zu stecken oder nicht), hat das Gewicht der Gegenstände im Rucksack viele Situationen, das heißt, er erreicht viele verschiedene Zustände, die entsprechen Der rekursive Baum hat viele verschiedene Knoten.
(2) Wir führen die wiederholten Zustände (Knoten) jeder Schicht zusammen, zeichnen nur die unterschiedlichen Zustände auf und leiten dann den Zustandssatz der nächsten Schicht basierend auf dem Zustandssatz der vorherigen Schicht ab. Wir können die wiederholten Zustände jeder Schicht zusammenführen, um sicherzustellen, dass die Anzahl der unterschiedlichen Zustände in jeder Schicht w nicht überschreitet (w stellt das Tragegewicht des Rucksacks dar), was im Beispiel 9 beträgt.
Dividieren Sie n Stufen. Jede Stufe wird basierend auf der vorherigen Stufe abgeleitet und schreitet dynamisch voran, um wiederholte Berechnungen zu vermeiden.
Die zeitliche Komplexität der Verwendung des Backtracking-Algorithmus zur Lösung dieses Problems beträgt O(2^n), was exponentiell ist. Wie hoch ist also die zeitliche Komplexität der dynamischen Programmierlösung?
Der zeitaufwändigste Teil ist die zweistufige for-Schleife im Code, daher die zeitliche Komplexität ist O(n*w). n stellt die Anzahl der Gegenstände dar und w stellt das Gesamtgewicht dar, das der Rucksack tragen kann. Wir müssen ein zusätzliches zweidimensionales Array von n mal w+1 beantragen, was viel Platz beansprucht. Daher werden wir manchmal sagen, dass dynamische Programmierung eine Lösung ist, die Raum gegen Zeit austauscht.
0-1 Aktualisierte Version des Rucksackproblems
Für eine Reihe unteilbarer Gegenstände mit unterschiedlichem Gewicht und unterschiedlichem Wert entscheiden wir uns dafür, einige Gegenstände in einen Rucksack zu packen. Unter der Voraussetzung, dass die maximale Gewichtsgrenze des Rucksacks eingehalten wird, wie hoch ist der maximale Gesamtwert der Gegenstände, die sein dürfen? im Rucksack verstaut?
Welche Probleme eignen sich zur Lösung durch dynamische Programmierung?
Drei Funktionen eines Modells
Ein Modell: mehrstufiges optimales Lösungsmodell für die Entscheidungsfindung
Drei Funktionen:
Optimale Unterstruktur, die optimale Lösung des Problems enthält die optimale Lösung des Unterproblems Keine Nachwirkungen, die erste Bedeutung ist, dass wir uns bei der Ableitung des Status der späteren Stufen nur um die vorherigen Stufen kümmern Dem Zustandswert ist es egal, wie dieser Zustand Schritt für Schritt abgeleitet wird. Die zweite Bedeutung besteht darin, dass der Status einer bestimmten Phase, sobald sie festgelegt ist, von Entscheidungen in nachfolgenden Phasen nicht mehr beeinflusst wird. (Letzteres hat keinen Einfluss auf das Vorhergehende.) Wiederholte Teilprobleme, unterschiedliche Entscheidungssequenzen, können beim Erreichen einer bestimmten gleichen Stufe zu wiederholten Zuständen führen. Zusammenfassung von zwei Ideen zur Lösung dynamischer Programmierprobleme
1. Zustandsübergangstabellenmethode
Im Allgemeinen können Probleme, die durch dynamische Programmierung gelöst werden können, durch Brute-Force-Suche mithilfe des Backtracking-Algorithmus gelöst werden. Zeichnen Sie den Rekursionsbaum. Anhand des Rekursionsbaums können wir leicht erkennen, ob es wiederholte Teilprobleme gibt und wie die wiederholten Teilprobleme generiert werden.
Nachdem wir das wiederholte Teilproblem gefunden haben, haben wir zwei Möglichkeiten, damit umzugehen. Die erste besteht darin, die Backtracking- und „Memo“-Methode direkt zu verwenden, um wiederholte Teilprobleme zu vermeiden. Hinsichtlich der Ausführungseffizienz unterscheidet sich dies nicht von der Lösungsidee der dynamischen Programmierung. Die zweite Methode ist die Verwendung der dynamischen Programmierung, der „Zustandsübergangstabellenmethode“.
2. Methode der Zustandsübergangsgleichung
Rekursion plus „Memo“ und die andere ist iterative Rekursion.
Methode der ZustandsübergangstabelleDie Problemlösungsidee lässt sich grob wie folgt zusammenfassen: Implementierung des Backtracking-Algorithmus – Definieren Sie den Zustand – Zeichnen Sie den Rekursionsbaum – Finden Sie doppelte Unterprobleme – Zeichnen Sie die Zustandsübergangstabelle – Füllen Sie die Tabelle entsprechend aus zur Rekursionsbeziehung – Übersetzen Sie den Tabellenfüllprozess in Code . Die allgemeine Idee der Zustandsübergangsgleichungsmethode kann wie folgt zusammengefasst werden: Finden Sie die optimale Unterstruktur – schreiben Sie die Zustandsübergangsgleichung – übersetzen Sie die Zustandsübergangsgleichung in Code.
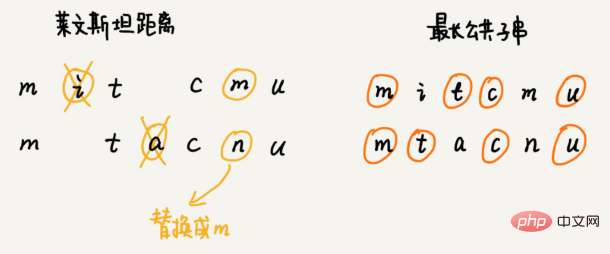
Bearbeitungsabstand bezieht sich auf die minimale Anzahl von Bearbeitungsvorgängen, die erforderlich sind, um eine Zeichenfolge in eine andere Zeichenfolge umzuwandeln (z. B. Hinzufügen eines Zeichens, Löschen eines Zeichens, Ersetzen eines Zeichens). Je größer der Bearbeitungsabstand, desto geringer die Ähnlichkeit zwischen den beiden Zeichenfolgen; umgekehrt gilt: Je kleiner der Bearbeitungsabstand, desto größer die Ähnlichkeit zwischen den beiden Zeichenfolgen. Für zwei identische Zeichenfolgen beträgt der Bearbeitungsabstand 0. Levenshtein-Distanz und Längste gemeinsame Teilstringlänge. Unter diesen ermöglicht der Levinstein-Abstand drei Bearbeitungsvorgänge zum Hinzufügen, Löschen und Ersetzen von Zeichen, und die Länge der längsten gemeinsamen Teilzeichenfolge ermöglicht nur zwei Bearbeitungsvorgänge zum Hinzufügen und Löschen von Zeichen. Wie berechnet man die Levenstein-Distanz programmgesteuert? Bei dieser Frage geht es darum, die Mindestanzahl an Bearbeitungen zu ermitteln, die erforderlich sind, um eine Zeichenfolge in eine andere zu ändern. Der gesamte Lösungsprozess umfasst mehrere Entscheidungsschritte. Wir müssen nacheinander untersuchen, ob jedes Zeichen in einer Zeichenfolge mit den Zeichen in einer anderen Zeichenfolge übereinstimmt, wie wir damit umgehen, wenn es übereinstimmt, und wie wir damit umgehen, wenn es nicht übereinstimmt . Daher entspricht dieses Problem dem „optimalen Lösungsmodell für mehrstufige Entscheidungsfindung“. Empfohlener Algorithmus Verwendet den Abstand von Vektoren, um die Ähnlichkeit zu finden. Wie findet man also schnell eine suboptimale Route, die nahe an der kürzesten Route liegt? Dieser schnelle Pfadplanungsalgorithmus ist der A*-Algorithmus, den wir heute lernen werden. Tatsächlich ist der A*-Algorithmus eine Optimierung und Transformation des Dijkstra-Algorithmus. Dies Der Abstand wird als aufgezeichnet (i stellt die Nummer dieses Scheitelpunkts dar), der Fachname ist heuristische Funktion (heuristische Funktion) Da die Berechnungsformel des euklidischen Abstands die zeitaufwändige Berechnung des Wurzelzeichens beinhaltet Daher verwenden wir im Allgemeinen eine andere einfachere Entfernungsberechnungsformel, nämlich die Manhattan-Entfernung (Manhattan-Entfernung). Manhattan-Entfernung ist die Summe der Abstände zwischen den horizontalen und vertikalen Koordinaten zwischen zwei Punkten. Der Berechnungsprozess umfasst nur Addition, Subtraktion und Vorzeichenbitumkehr und ist daher effizienter als die euklidische Distanz. int hManhattan(Vertex v1, Vertex v2) { // Vertex stellt den Scheitelpunkt dar, der später definiert wird
Rückgabe Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);
}
f(i)=g(i)+h(i), die Pfadlänge g(i) zwischen dem Scheitelpunkt und dem Startpunkt und die geschätzte Pfadlänge vom Scheitelpunkt bis zum Endpunkt h(i). Der professionelle Name von f(i) ist Die Methode ist die Bewertungsfunktion. Ein*-Algorithmus ist eine einfache Modifikation des Dijkstra-Algorithmus. Das kleinste f(i) wird zuerst aufgeführt. Es gibt drei Hauptunterschiede zwischen ihm und der Code-Implementierung des Dijkstra-Algorithmus: 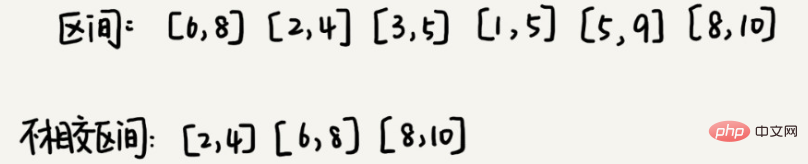
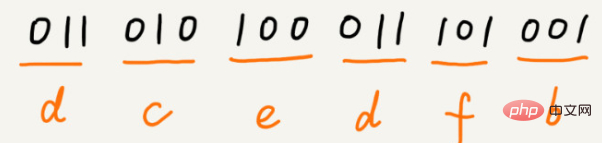
hat eine Zerlegungsbeendigungsbedingung, das heißt, wenn das Problem klein genug ist, kann es direkt gelöst werden;#🎜🎜 #
 Suche: Wie verwende ich den A*-Suchalgorithmus, um die Pfadfindungsfunktion im Spiel zu implementieren?
Suche: Wie verwende ich den A*-Suchalgorithmus, um die Pfadfindungsfunktion im Spiel zu implementieren? 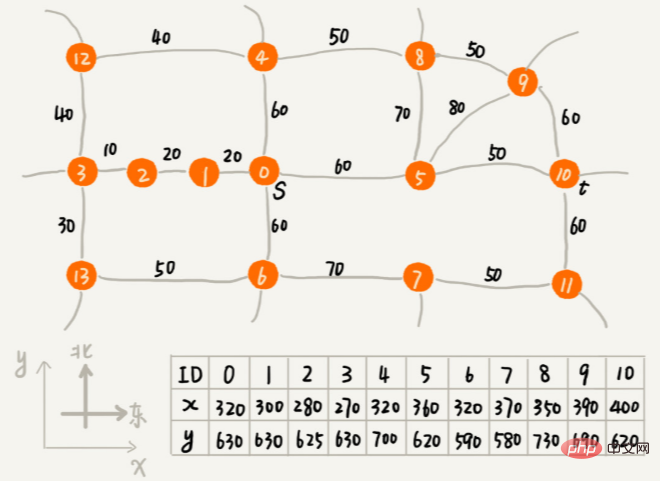 Schätzen Sie ungefähr die Pfadlänge zwischen dem Scheitelpunkt und dem Endpunkt anhand des geradlinigen Abstands zwischen dem Scheitelpunkt und dem Endpunkt, der der euklidische Abstand ist (Hinweis: Pfadlänge und geradliniger Abstand sind zwei Konzepte)
Schätzen Sie ungefähr die Pfadlänge zwischen dem Scheitelpunkt und dem Endpunkt anhand des geradlinigen Abstands zwischen dem Scheitelpunkt und dem Endpunkt, der der euklidische Abstand ist (Hinweis: Pfadlänge und geradliniger Abstand sind zwei Konzepte) Die Art und Weise, wie die Prioritätswarteschlange aufgebaut ist, ist unterschiedlich. Der A*-Algorithmus erstellt eine Prioritätswarteschlange basierend auf dem f-Wert (d. h. f(i)=g(i)+h(i) gerade erwähnt), während der Dijkstra-Algorithmus eine Prioritätswarteschlange basierend auf dem dist-Wert erstellt ( Das heißt, das gerade erwähnte g (i)) zum Erstellen einer Prioritätswarteschlange.
Das obige ist der detaillierte Inhalt vonWelche gängigen Algorithmen werden in der Java-Entwicklung häufig verwendet?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

