So zeichnen Sie fraktale Muster mit Python

1. Ziel

Schreiben Sie ein Programm, das ein gleichseitiges Dreieck zeichnen kann und auf jeder Seite des Dreiecks ein etwas kleineres, nach außen gerichtetes Dreieck zeichnen kann. Durch die Möglichkeit, diesen Vorgang beliebig oft zu wiederholen, entstehen einige interessante Muster.

2. Stellen Sie das Bild dar

Stellen Sie das Bild als zweidimensionales Pixelarray dar. Jede Zelle im Pixelarray repräsentiert die Farbe (RGB) dieses Pixels.

Dazu können Sie die NumPy-Bibliothek verwenden, um ein Pixel-Array zu generieren, und Pillow, um es in ein speicherbares Bild umzuwandeln.

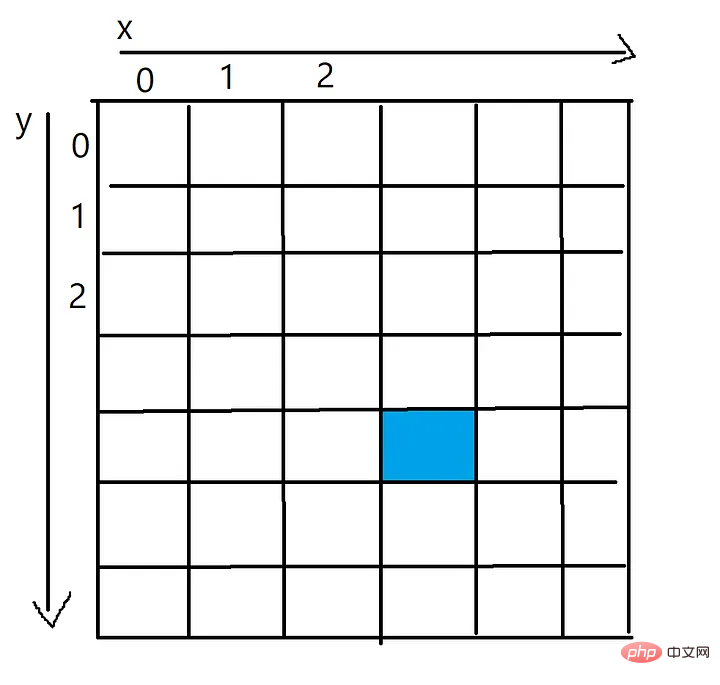
Der x-Wert des blauen Pixels ist 3 und der y-Wert ist 4, auf den über ein zweidimensionales Array zugegriffen werden kann, z. B. pixels[4][3]

Drei, zeichnen Sie eine Linie

Beginnen Sie nun mit dem Codieren. Sie benötigen zunächst eine Funktion, die zwei Koordinatensätze annehmen und eine Linie zwischen ihnen zeichnen kann.

Der folgende Code interpoliert zwischen zwei Punkten und fügt bei jedem Schritt neue Pixel zum Pixelarray hinzu. Sie können sich diesen Vorgang als Pixel für Pixel auf einer Linie vorstellen.

Sie können das fortlaufende Zeichen „“ in jedem Codeausschnitt verwenden, um einige längere Codezeilen unterzubringen.

import numpy as np
from PIL import Image
import math
def plot_line(from_coordinates, to_coordinates, thickness, colour, pixels):
    # 找出像素阵列的边界
    max_x_coordinate = len(pixels[0])
    max_y_coordinate = len(pixels)
    # 两点之间沿着x轴和y轴的距离
    horizontal_distance = to_coordinates[1] - from_coordinates[1]
    vertical_distance = to_coordinates[0] - from_coordinates[0]
    # 两点之间的总距离
    distance =  math.sqrt((to_coordinates[1] - from_coordinates[1])**2 \
                + (to_coordinates[0] - from_coordinates[0])**2)
    # 每次给一个新的像素上色时，将向前走多远
    horizontal_step = horizontal_distance/distance
    vertical_step = vertical_distance/distance
    # 此时，将进入循环以在像素数组中绘制线
    # 循环的每一次迭代都会沿着线添加一个新的点
    for i in range(round(distance)):
        # 这两个坐标是直线中心的坐标
        current_x_coordinate = round(from_coordinates[1] + (horizontal_step*i))
        current_y_coordinate = round(from_coordinates[0] + (vertical_step*i))
        # 一旦得到了点的坐标，
        # 就在坐标周围画出尺寸为thickness的图案
        for x in range (-thickness, thickness):
            for y in range (-thickness, thickness):
                x_value = current_x_coordinate + x
                y_value = current_y_coordinate + y
                if (x_value > 0 and x_value < max_x_coordinate and \
                    y_value > 0 and y_value < max_y_coordinate):
                    pixels[y_value][x_value] = colour
# 定义图像的大小
pixels = np.zeros( (500,500,3), dtype=np.uint8 )
# 画一条线
plot_line([0,0], [499,499], 1, [255,200,0], pixels)
# 把像素阵列变成一张真正的图片
img = Image.fromarray(pixels)
# 显示得到的图片，并保存它
img.show()
img.save(&#39;Line.png&#39;)

Das Ergebnis dieser Funktion beim Zeichnen einer gelben Linie zwischen jeder Ecke des Pixelarrays

4 Zeichnen eines Dreiecks

Da es nun eine Funktion gibt, die eine Linie zwischen zwei Punkten zeichnen kann, können Sie zeichnen das dritte Ein gleichseitiges Dreieck.

Angesichts des Mittelpunkts und der Seitenlängen eines Dreiecks kann die Höhe mit der Formel berechnet werden: h = ½(√3a).

Anhand dieser Höhe, des Mittelpunkts und der Seitenlängen können Sie nun die Position jeder Ecke des Dreiecks berechnen. Mit der Funktion plot_line, die wir zuvor erstellt haben, können wir eine Linie zwischen den einzelnen Ecken zeichnen. plot_line函数，可以在每个角之间画一条线。

def draw_triangle(center, side_length, thickness, colour, pixels):
    # 等边三角形的高度是，h = ½(√3a)
    # 其中a是边长
    triangle_height = round(side_length * math.sqrt(3)/2)
    # 顶角
    top = [center[0] - triangle_height/2, center[1]]
    # 左下角
    bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
    # 右下角
    bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
    # 在每个角之间画一条线来完成三角形
    plot_line(top, bottom_left, thickness, colour, pixels)
    plot_line(top, bottom_right, thickness, colour, pixels)
    plot_line(bottom_left, bottom_right, thickness, colour, pixels)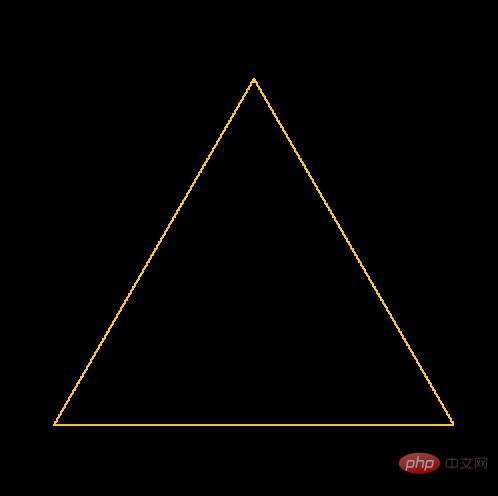

在500x500像素PNG的中心绘制三角形时的结果

五、生成分形

一切都已准备就绪，可以用Python创建第一个分形。

但是最后一步是最难完成的，三角形函数为它的每一边调用自己，需要能够计算每个新的较小三角形的中心点，并正确地旋转它们，使它们垂直于它们所附着的一侧。

通过从旋转的坐标中减去中心点的偏移量，然后应用公式来旋转一对坐标，可以用这个函数来旋转三角形的每个角。

def rotate(coordinate, center_point, degrees):
    # 从坐标中减去旋转的点
    x = (coordinate[0] - center_point[0])
    y = (coordinate[1] - center_point[1])
    # Python的cos和sin函数采用弧度而不是度数
    radians = math.radians(degrees)
    # 计算旋转点
    new_x = (x * math.cos(radians)) - (y * math.sin(radians))
    new_y = (y * math.cos(radians)) + (x * math.sin(radians))
    # 将在开始时减去的偏移量加回旋转点上
    return [new_x + center_point[0], new_y + center_point[1]]

将每个坐标旋转35度的三角形

可以旋转一个三角形后，思考如何在第一个三角形的每条边上画一个新的小三角形。

为了实现这一点，扩展draw_triangle函数，为每条边计算一个新三角形的旋转和中心点，其边长被参数shrink_side_by减少。

一旦它计算出新三角形的中心点和旋转，它就会调用draw_triangle（自身）来从当前线的中心画出新的、更小的三角形。然后，这将反过来打击同一个代码块，为一个更小的三角形计算另一组中心点和旋转。

这就是所谓的循环算法，因为draw_triangle

def draw_triangle(center, side_length, degrees_rotate, thickness, colour, \
                  pixels, shrink_side_by, iteration, max_depth):
    # 等边三角形的高度是，h = ½(√3a)
    # 其中'a'是边长
    triangle_height = side_length * math.sqrt(3)/2
    # 顶角
    top = [center[0] - triangle_height/2, center[1]]
    # 左下角
    bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
    # 右下角
    bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
    if (degrees_rotate != 0):
        top = rotate(top, center, degrees_rotate)
        bottom_left = rotate(bottom_left, center, degrees_rotate)
        bottom_right = rotate(bottom_right, center, degrees_rotate)
    # 三角形各边之间的坐标
    lines = [[top, bottom_left],[top, bottom_right],[bottom_left, bottom_right]]
    line_number = 0
    # 在每个角之间画一条线来完成三角形
    for line in lines:
        line_number += 1
        plot_line(line[0], line[1], thickness, colour, pixels)
        # 如果还没有达到max_depth，就画一些新的三角形
        if (iteration < max_depth and (iteration < 1 or line_number < 3)):
            gradient = (line[1][0] - line[0][0]) / (line[1][1] - line[0][1])
            new_side_length = side_length*shrink_side_by
            # 正在绘制的三角形线的中心
            center_of_line = [(line[0][0] + line[1][0]) / 2, \
                              (line[0][1] + line[1][1]) / 2]
            new_center = []
            new_rotation = degrees_rotate
            # 需要旋转traingle的数量
            if (line_number == 1):
                new_rotation += 60
            elif (line_number == 2):
                new_rotation -= 60
            else:
                new_rotation += 180
            # 在一个理想的世界里，这将是gradient=0，
            # 但由于浮点除法的原因，无法
            # 确保永远是这种情况
            if (gradient < 0.0001 and gradient > -0.0001):
                if (center_of_line[0] - center[0] > 0):
                    new_center = [center_of_line[0] + triangle_height * \
                                 (shrink_side_by/2), center_of_line[1]]
                else:
                    new_center = [center_of_line[0] - triangle_height * \
                                  (shrink_side_by/2), center_of_line[1]]
            else:
                # 计算直线梯度的法线
                difference_from_center = -1/gradient
                # 计算这条线距中心的距离
                # 到新三角形的中心
                distance_from_center = triangle_height * (shrink_side_by/2)
                # 计算 x 方向的长度，
                # 从线的中心到新三角形的中心
                x_length = math.sqrt((distance_from_center**2)/ \
                                     (1 + difference_from_center**2))
                # 计算出x方向需要走哪条路
                if (center_of_line[1] < center[1] and x_length > 0):
                    x_length *= -1
                # 现在计算Y方向的长度
                y_length = x_length * difference_from_center
                # 用新的x和y值来偏移线的中心
                new_center = [center_of_line[0] + y_length, \
                              center_of_line[1] + x_length]
            draw_triangle(new_center, new_side_length, new_rotation, \
                          thickness, colour, pixels, shrink_side_by, \
                          iteration+1, max_depth)

in 500x500 Pixel PNG Das Ergebnis beim Zeichnen eines Dreiecks in der Mitte

5. Fraktal generieren

🎜 Alles ist bereit, um das erste Fraktal in Python zu erstellen. 🎜🎜Aber der letzte Schritt ist am schwierigsten zu erledigen, die Dreiecksfunktion ruft sich für jede Seite davon auf, man muss in der Lage sein, den Mittelpunkt jedes neuen kleineren Dreiecks zu berechnen und sie richtig zu drehen, damit sie senkrecht zu der einen sind Sie sind an der Seite befestigt. 🎜🎜Mit dieser Funktion können Sie jede Ecke eines Dreiecks drehen, indem Sie den Versatz des Mittelpunkts von den gedrehten Koordinaten subtrahieren und dann die Formel zum Drehen eines Koordinatenpaars anwenden. 🎜rrreee🎜🎜🎜Konvertieren Sie jedes Koordinate Ein Dreieck um 35 Grad drehen🎜🎜Überlegen Sie nach dem Drehen eines Dreiecks, wie Sie auf jeder Seite des ersten Dreiecks ein neues kleines Dreieck zeichnen. 🎜🎜Um dies zu erreichen, erweitern Sie die Funktion draw_triangle, um die Drehung und den Mittelpunkt eines neuen Dreiecks für jede Seite zu berechnen, dessen Seitenlängen um den Parameter shrink_side_by reduziert werden. 🎜🎜Sobald der Mittelpunkt und die Drehung des neuen Dreiecks berechnet wurden, ruft es draw_triangle(self) auf, um das neue, kleinere Dreieck vom Mittelpunkt der aktuellen Linie aus zu zeichnen. Dadurch wird dann derselbe Codeblock in umgekehrter Reihenfolge aufgerufen, um einen weiteren Satz von Mittelpunkten und Drehungen für ein kleineres Dreieck zu berechnen. 🎜🎜Dies wird als Schleifenalgorithmus bezeichnet, da sich die Funktion draw_triangle nun selbst aufruft, bis sie die maximale Tiefe des Dreiecks erreicht, das sie zeichnen möchte. Dieser Escape-Satz ist wichtig, da die Funktion theoretisch eine ewige Schleife ausführen würde (in der Praxis würde der Aufrufstapel jedoch zu groß werden, was zu einem Stapelüberlauffehler führen würde). 🎜rrreee🎜🎜🎜🎜Dreieckiges Fraktal, schrumpfende Seiten = 1/2, maximale Tiefe = 2🎜

Das obige ist der detaillierte Inhalt vonSo zeichnen Sie fraktale Muster mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!