So implementieren Sie Dichotomie in Java

Finden Sie in einem geordneten Array heraus, ob eine bestimmte Zahl vorhanden ist

Idee:

• Da es sich um ein geordnetes Array handelt, können Sie zuerst die Mittelpunktposition ermitteln und der Mittelpunkt kann das Array in links unterteilen und rechte Hälften.

• Wenn der Wert der Mittelpunktposition gleich dem Zielwert ist, geben Sie die Mittelpunktposition direkt zurück.

• Wenn der Wert der Mittelpunktposition kleiner als der Zielwert ist, gehen Sie zur linken Seite des Mittelpunkts des Arrays und suchen Sie auf die gleiche Weise.

• Wenn der Wert der Mittelpunktposition größer als der Zielwert ist, nehmen Sie die rechte Seite des Mittelpunkts des Arrays und suchen Sie auf die gleiche Weise.

• Wenn am Ende nicht gefunden, geben Sie Folgendes zurück: -1.

Code

class Solution {
    public int search(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
                return m;
            } else if (arr[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

Zeitkomplexität O(logN). O(logN)。

在一个有序数组中，找大于等于某个数最左侧的位置

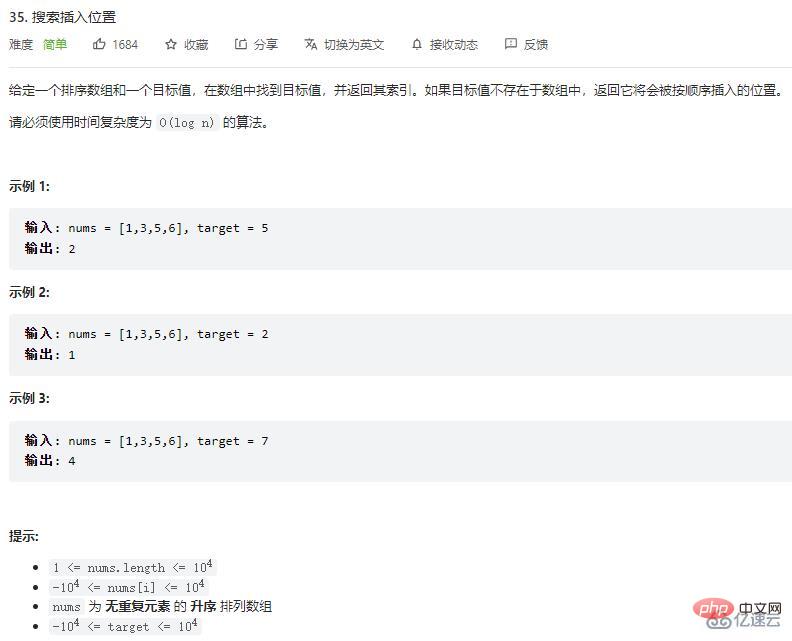
示例 1:

输入: nums = [1,3,5,6], target = 5

输出: 2

说明：如果要在num这个数组中插入 5 这个元素，应该是插入在元素 3 和 元素 5 之间的位置，即 2 号位置。

示例 2:

输入: nums = [1,3,5,6], target = 2

输出: 1

说明：如果要在num这个数组中插入 2 这个元素，应该是插入在元素 1 和 元素 3 之间的位置，即 1 号位置。

示例 3:

输入: nums = [1,3,5,6], target = 7

输出: 4

说明：如果要在num这个数组中插入 7 这个元素，应该是插入在数组末尾，即 4 号位置。

通过上述示例可以知道，这题本质上就是求在一个有序数组中，找大于等于某个数最左侧的位置，如果不存在，就返回数组长度（表示插入在最末尾位置）

我们只需要在上例基础上进行简单改动即可，上例中，我们找到满足条件的位置就直接return了

if (arr[m] == t) {
    return m;
}

在本问题中，因为要找到最左侧的位置，所以，在遇到相等的时候，只需要先把位置记录下来，不用直接返回，然后继续去左侧找是否还有满足条件的更左边的位置。

同时，在遇到arr[m] > t条件下，也需要记录下此时的m位置，因为这也可能是满足条件的位置。

代码：

class Solution {
    public static int searchInsert(int[] arr, int t) {
        int ans = arr.length;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l)>>1);
            if (arr[m] >= t) {
                ans = m;
                r = m - 1;
            } else  {
                l = m + 1;
            } 
        }
        return ans;
    }
}

整个算法的时间复杂度是O(logN)。

在排序数组中查找元素的第一个和最后一个位置

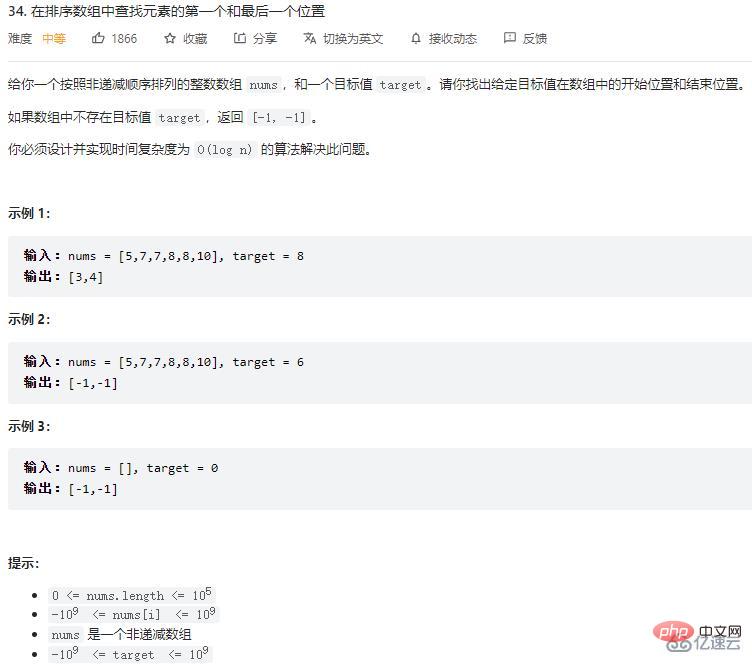
思路

本题也是用二分来解，当通过二分找到某个元素的时候，不急着返回，而是继续往左（右）找，看能否找到更左（右）位置匹配的值。

代码如下：

class Solution {
    public static int[] searchRange(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return new int[]{-1, -1};
        }
        return new int[]{left(arr,t),right(arr,t)};   
    }
    public static int left(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               r = m - 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
    public static int right(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               l = m + 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
}

时间复杂度 O(logN)。

局部最大值问题

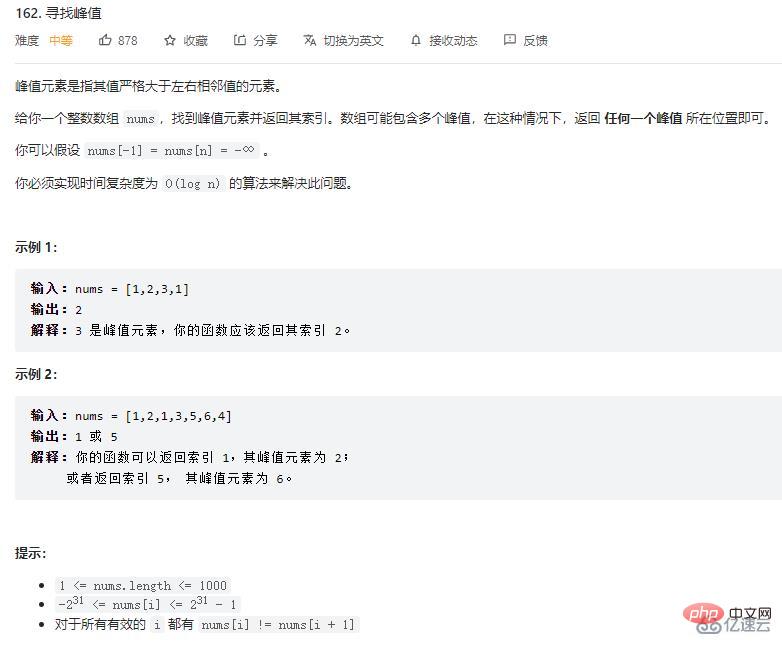
思路

假设数组长度为N，首先判断0号位置的数和N-1位置的数是不是峰值位置。

0号位置只需要和1号位置比较，如果0号位置大，0号位置就是峰值位置，可以直接返回。

N-1号位置只需要和N-2号位置比较，如果N-1号位置大，N-1号位置就是峰值位置，可以直接返回。

如果0号位置和N-1在上轮比较中均是最小值，那么数组的样子必然是如下情况：

由上图可知，[0..1]区间内是增长趋势, [N-2...N-1]区间内是下降趋势。

那么峰值位置必在[1...N-2]之间出现。

此时可以通过二分来找峰值位置，先来到中点位置，假设为mid，如果中点位置的值比左右两边的值都大:

arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]

则mid位置即峰值位置，直接返回。

否则，有如下两种情况：

情况一：mid 位置的值比 mid - 1 位置的值小

趋势如下图：

则在[1...(mid-1)]

Suchen Sie in einem geordneten Array die Position ganz links, die größer oder gleich einer bestimmten Zahl ist

Beispiel 1:

Eingabe: nums = [1,3,5,6], Ziel = 5

🎜Ausgabe: 2🎜🎜Erläuterung: Wenn Sie möchten verwenden numDas in dieses Array eingefügte Element 5 sollte an der Position zwischen Element 3 und Element 5, also Position 2, eingefügt werden. 🎜🎜Beispiel 2:🎜🎜Eingabe: nums = [1,3,5,6], Ziel = 2🎜🎜Ausgabe: 1🎜🎜Erläuterung: Wenn Sie 2 in das Array num einfügen möchten Das Element sollte zwischen Element 1 und Element 3, also Position 1, eingefügt werden. 🎜🎜Beispiel 3:🎜🎜Eingabe: nums = [1,3,5,6], Ziel = 7🎜🎜Ausgabe: 4🎜🎜Erläuterung: Wenn Sie 7 in das Array num einfügen möchten Das Element sollte am Ende des Arrays eingefügt werden, also an Position 4. 🎜🎜Aus dem obigen Beispiel können Sie erkennen, dass der Kern dieser Frage darin besteht, die Position ganz links in einem geordneten Array zu finden, die größer oder gleich einer bestimmten Zahl ist. Wenn sie nicht vorhanden ist, geben Sie die Länge des Arrays zurück (angeben). dass es am Ende eingefügt wird (Position)🎜🎜Wir müssen nur einfache Änderungen basierend auf dem obigen Beispiel vornehmen. Wenn wir im obigen Beispiel die Position finden, die die Bedingungen erfüllt, kehren wir direkt zurück🎜

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

🎜In dieser Frage müssen Sie die Position ganz links finden. Wenn Sie also auf Gleichheit stoßen, müssen Sie zunächst nur die Position aufzeichnen, ohne direkt zurückzukehren, und dann weiter nach links gehen, um herauszufinden, ob sie vorhanden ist ist eine linke Position, die die Bedingungen erfüllt. 🎜🎜Wenn Sie gleichzeitig auf arr[m] > t stoßen, müssen Sie zu diesem Zeitpunkt auch die Position von m aufzeichnen, da dies der Fall sein kann Es muss sich auch um einen Standort handeln, der die Bedingungen erfüllt. 🎜🎜Code: 🎜rrreee🎜Die zeitliche Komplexität des gesamten Algorithmus beträgt O(logN). 🎜🎜Finden Sie die erste und letzte Position eines Elements in einem sortierten Array🎜🎜🎜🎜Denken🎜🎜Diese Frage wird auch durch Dichotomie gelöst. Wenn ein Element durch Dichotomie gefunden wird, eilen Sie nicht zurück, sondern suchen Sie weiter nach links (rechts), um zu sehen, ob Sie es finden können mehr Der Wert, der für die linke (rechte) Position abgeglichen werden soll. 🎜🎜Der Code lautet wie folgt: 🎜rrreee🎜Zeitkomplexität O(logN). 🎜🎜Lokales Maximumproblem🎜🎜🎜🎜 Idee 🎜🎜 Angenommen, die Länge des Arrays beträgt N. Bestimmen Sie zunächst, ob die Zahl an der Position 0 und die Zahl an der Position N-1 Position sind Spitzenpositionen. 🎜🎜Die 0-Position muss nur mit der 1-Position verglichen werden. Wenn die 0-Position größer ist, wird die 0-Position verwendet. code> position Dies ist die Spitzenposition und kann direkt zurückgegeben werden. 🎜🎜Die N-1-Position muss nur mit der N-2-Position verglichen werden. Wenn die N-1-Position größer ist, N Position -1 ist die Spitzenposition und kann direkt zurückgegeben werden. 🎜🎜Wenn die Position 0 und N-1 beide Mindestwerte in der letzten Vergleichsrunde sind, dann muss das Array wie folgt aussehen: 🎜🎜🎜🎜Wie aus dem obigen Bild ersichtlich ist, [0..1 ]Das Intervall ist ein wachsender Trend und das [N-2...N-1]Intervall ist ein Abwärtstrend. 🎜🎜Dann muss die Peak-Position zwischen [1...N-2] liegen. 🎜🎜Zu diesem Zeitpunkt können Sie die Spitzenposition durch Halbierung ermitteln. Gehen Sie zunächst zur Mittelpunktposition, vorausgesetzt, dass diese mitte ist als die Werte auf der linken und rechten Seite:🎜rrreee🎜Die mittlere-Position ist die Spitzenposition und wird direkt zurückgegeben. 🎜🎜Ansonsten gibt es die folgenden zwei Situationen: 🎜🎜Fall 1: Der Wert der Mittelposition ist kleiner als der Wert der Mittelposition 1 🎜🎜Der Trend ist wie folgt: 🎜🎜🎜🎜 wird innerhalb des [1...(mid-) fortgesetzt 1)] Intervall Zwei Punkte. 🎜🎜Fall 2: Der Wert der Mittelposition ist kleiner als der Wert der Mittelposition + 1🎜🎜Der Trend ist: 🎜🎜🎜🎜

则在[(mid+1)...(N-2)]区间内继续上述二分。

完整代码

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

时间复杂度O(logN)。

Das obige ist der detaillierte Inhalt vonSo implementieren Sie Dichotomie in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!