Clustering-Algorithmus basierend auf der Projektion auf konvexe Mengen (POCS)

POCS: Projektionen auf konvexe Mengen. In der Mathematik ist eine konvexe Menge eine Menge, in der jedes Liniensegment zwischen zwei beliebigen Punkten innerhalb der Menge liegt. Unter Projektion versteht man die Abbildung eines Punktes auf einen Unterraum in einem anderen Raum. Bei einer gegebenen konvexen Menge und einem Punkt können Sie die Projektion des Punktes auf die konvexe Menge ermitteln. Die Projektion ist der Punkt in der konvexen Menge, der dem Punkt am nächsten liegt, und kann berechnet werden, indem der Abstand zwischen diesem Punkt und jedem anderen Punkt in der konvexen Menge minimiert wird. Da es sich um eine Projektion handelt, können wir die Merkmale einer konvexen Menge in einem anderen Raum zuordnen, sodass Operationen wie Clustering oder Dimensionsreduzierung durchgeführt werden können.

In diesem Artikel wird ein Clustering-Algorithmus beschrieben, der auf der konvexen Mengenprojektionsmethode basiert, dh ein Clustering-Algorithmus, der auf POCS basiert. Das Originalpapier wurde auf der IWIS2022 veröffentlicht.

Konvexe Menge

Eine konvexe Menge ist als eine Menge von Datenpunkten definiert, in der das Liniensegment, das zwei beliebige Punkte x1 und x2 in der Menge verbindet, vollständig in dieser Menge enthalten ist. Gemäß der Definition einer konvexen Menge werden die leere Menge ∅, die einheitliche Menge, das Liniensegment, die Hyperebene und die euklidische Kugel alle als konvexe Mengen betrachtet. Ein Datenpunkt wird auch als konvexe Menge betrachtet, da es sich um eine Singleton-Menge (eine Menge mit nur einem Element) handelt. Dies eröffnet einen neuen Weg für die Anwendung des POCS-Konzepts auf geclusterte Datenpunkte.

Projektion konvexer Mengen (POCS)

POCS-Methoden können grob in zwei Typen unterteilt werden: alternierend und parallel.

1. Alternierender POC

Ausgehend von einem beliebigen Punkt im Datenraum konvergiert die alternierende Projektion von diesem Punkt auf zwei (oder mehr) sich schneidende konvexe Mengen zu einem Punkt innerhalb des Mengenschnittpunkts, wie in der folgenden Abbildung:

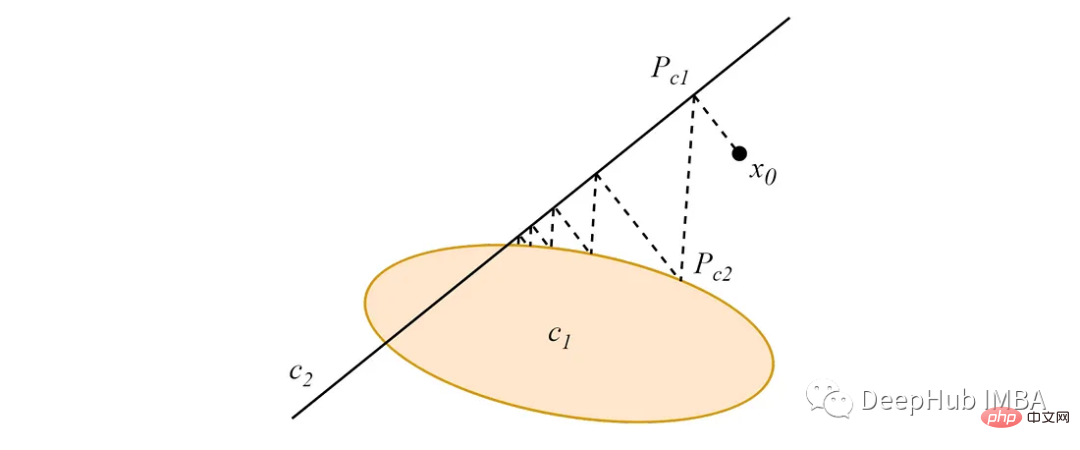
Wenn die konvexen Mengen disjunkt sind, konvergieren alternierende Projektionen zu gierigen Grenzzyklen, die von der Projektionsreihenfolge abhängen.

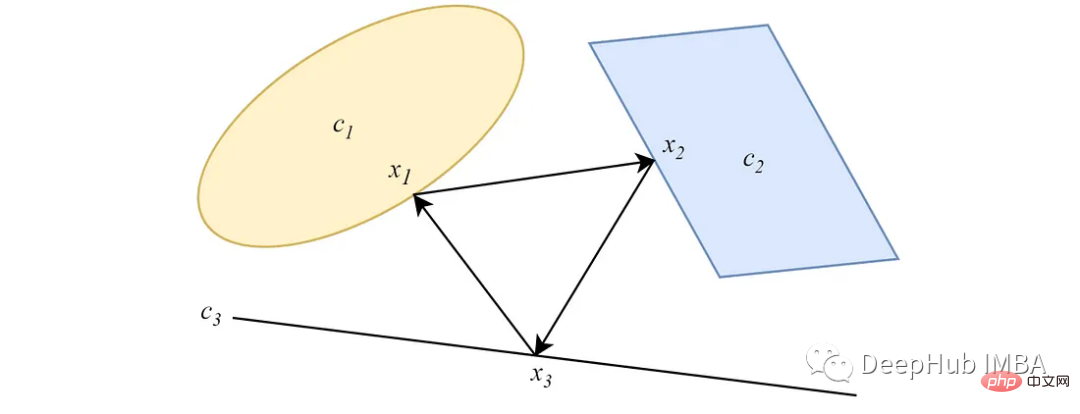
2. Parallele POCS

Im Gegensatz zur alternierenden Form projizieren parallele POCS von Datenpunkten gleichzeitig auf alle konvexen Mengen, und jede Projektion hat ein Wichtigkeitsgewicht. Bei zwei nicht leeren, sich schneidenden konvexen Mengen konvergiert die Parallelprojektion ähnlich wie bei der alternierenden Version zu einem Punkt am Schnittpunkt der Mengen.

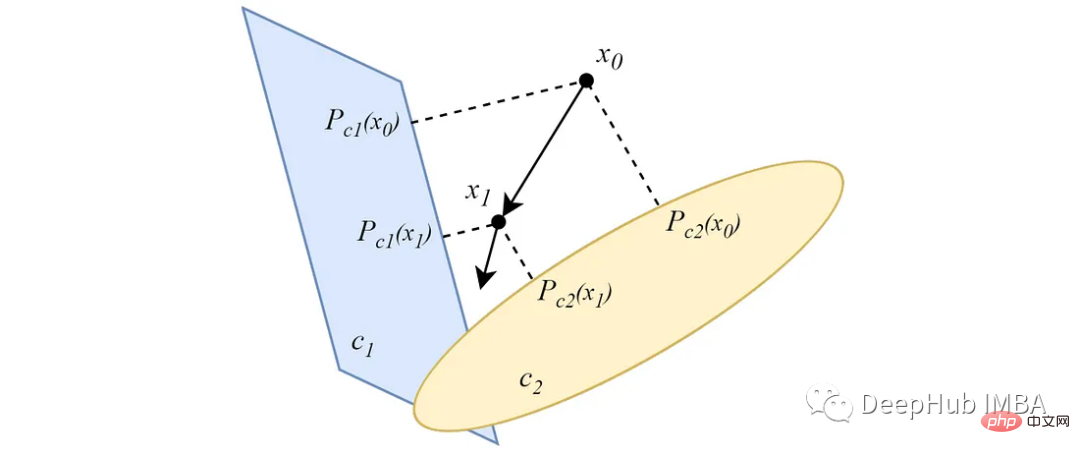
Wenn sich die konvexen Mengen nicht schneiden, konvergiert die Projektion zu einer Minimallösung. Die Hauptidee des POC-basierten Clustering-Algorithmus ergibt sich aus dieser Funktion.

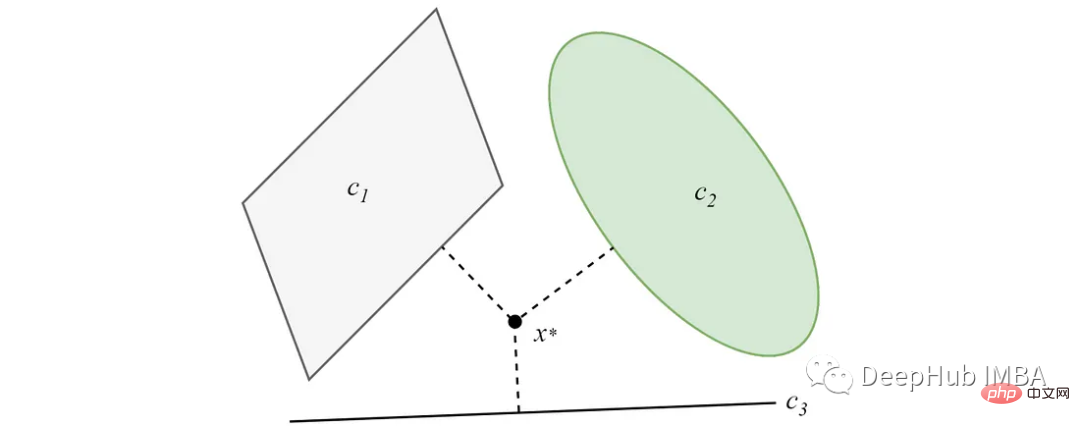
Weitere Informationen zu POCS finden Sie im Originalpapier.

Auf POCs basierender Clustering-Algorithmus.

Der Autor des Papiers nutzte die Konvergenz der parallelen POCS-Methode und schlug einen sehr einfachen, aber effektiven Clustering-Algorithmus vor bis zu einem gewissen Grad Klassenalgorithmus. Der Algorithmus funktioniert ähnlich wie der klassische K-Means-Algorithmus, es gibt jedoch Unterschiede in der Art und Weise, wie jeder Datenpunkt verarbeitet wird: Der K-Means-Algorithmus gewichtet die Wichtigkeit jedes Datenpunkts gleich, der POCs-basierte Clustering-Algorithmus hingegen jeden Datenpunkt wird unterschiedlich gewichtet, was proportional zur Entfernung des Datenpunkts vom Cluster-Prototyp ist.

Der Pseudocode des Algorithmus lautet wie folgt:

Experimentelle Ergebnisse

Der Autor testete die Leistung des POCs-basierten Clustering-Algorithmus anhand einiger öffentlicher Benchmark-Datensätze. Die folgende Tabelle fasst die Beschreibungen dieser Datensätze zusammen.

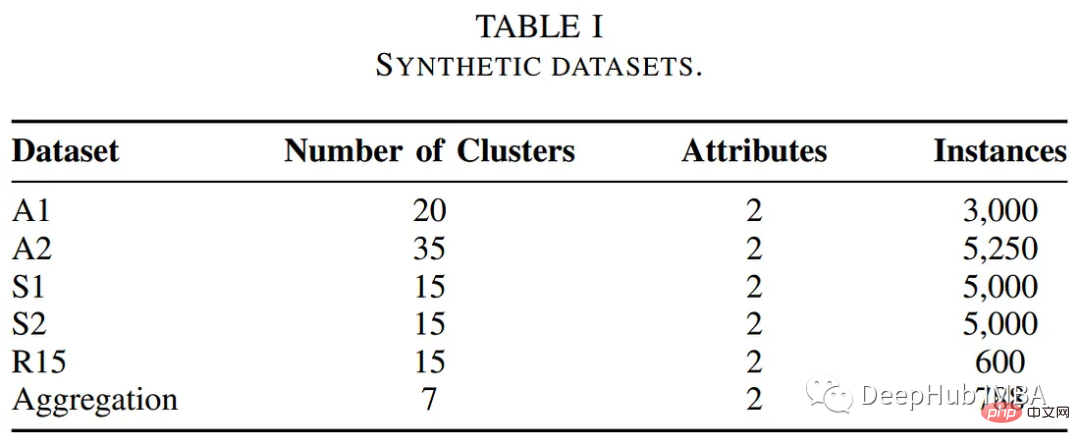
Der Autor verglich die Leistung des POCs-basierten Clustering-Algorithmus mit anderen herkömmlichen Clustering-Methoden, einschließlich K-Means- und Fuzzy-C-Means-Algorithmen. Die folgende Tabelle fasst die Bewertung hinsichtlich Ausführungszeit und Clusterfehler zusammen.

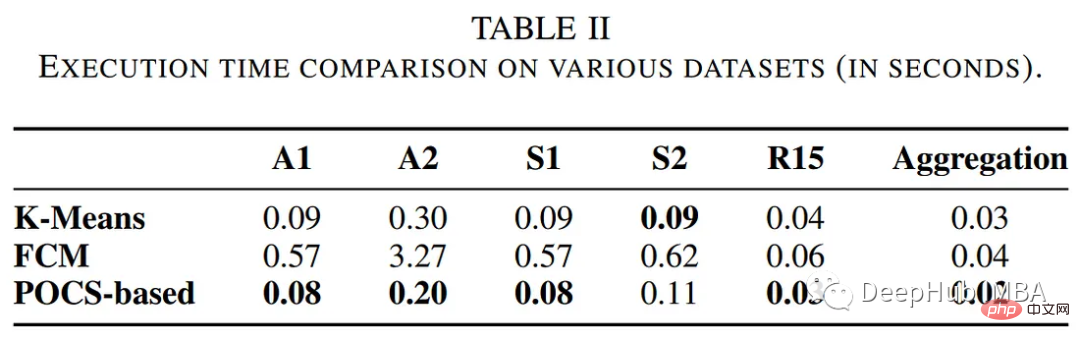
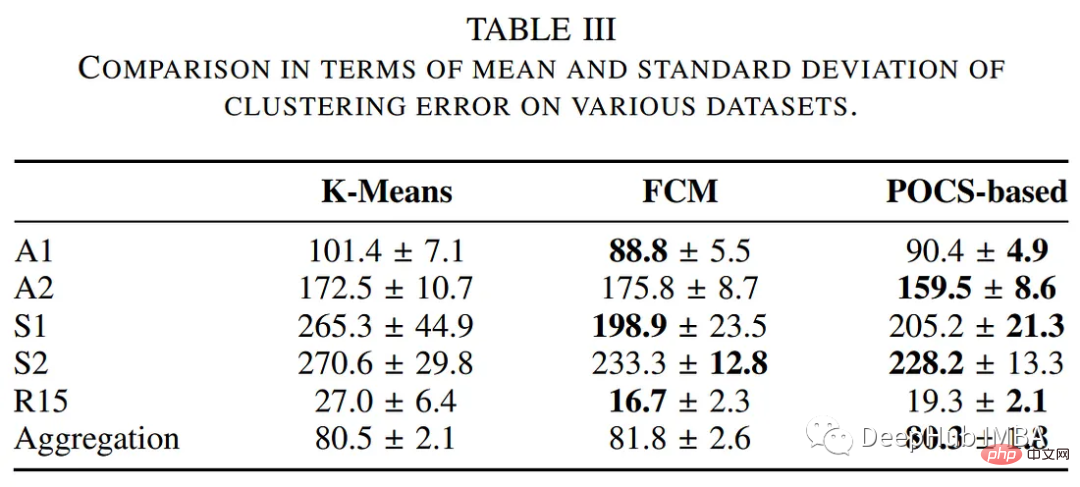
Die Clustering-Ergebnisse werden unten angezeigt:

Beispielcode

Wir verwenden diesen Algorithmus für einen sehr einfachen Datensatz. Der Autor hat ein Paket zur direkten Verwendung veröffentlicht, das wir direkt für Anwendungen verwenden können:

pip install pocs-based-clustering

Erstellen Sie einen einfachen Datensatz von 5000 Datenpunkten, zentriert auf 10 Clustern:

# Import packages
 import time
 import matplotlib.pyplot as plt
 
 from sklearn.datasets import make_blobs
 from pocs_based_clustering.tools import clustering
 
 
 # Generate a simple dataset
 num_clusters = 10
 X, y = make_blobs(n_samples=5000, centers=num_clusters, 
 cluster_std=0.5, random_state=0)
 
 plt.figure(figsize=(8,8))
 plt.scatter(X[:, 0], X[:, 1], s=50)
 plt.show()

Führen Sie Clustering durch und zeigen Sie die Ergebnisse an:

# POSC-based Clustering Algorithm
 centroids, labels = clustering(X, num_clusters, 100)
 
 # Display results
 plt.figure(figsize=(8,8))
 plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
 plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red')
 plt.show()

总结

我们简要回顾了一种简单而有效的基于投影到凸集(POCS)方法的聚类技术，称为基于POCS的聚类算法。该算法利用POCS的收敛特性应用于聚类任务，并在一定程度上实现了可行的改进。在一些基准数据集上验证了该算法的有效性。

论文的地址如下：https://arxiv.org/abs/2208.08888

作者发布的源代码在这里：https://github.com/tranleanh/pocs-based-clustering

Das obige ist der detaillierte Inhalt vonClustering-Algorithmus basierend auf der Projektion auf konvexe Mengen (POCS). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!