So finden Sie den minimalen Spanning Tree in Java
- WBOYnach vorne
- 2023-04-29 18:58:13723Durchsuche
1 Übersicht über den minimalen Spannbaum
Spannbaum (SpanningTree): Der Spannbaum eines verbundenen Diagramms bezieht sich auf a Verbundener Graph Ein Untergraph, der alle n Eckpunkte im Graphen enthält, aber nur n-1 Kanten, die ausreichen, um einen Baum zu bilden. Ein Spannbaum mit n Eckpunkten hat nur n-1 Kanten. Wenn dem Spannbaum eine weitere Kante hinzugefügt wird, bildet er definitiv einen Kreis.
Minimaler Spannbaum: Unter allen Spannbäumen in einem verbundenen Diagramm wird das Gewicht aller Kanten und der kleinste Spannbaum als minimaler Spannbaum bezeichnet.
Im Leben sind grafische Strukturen am weitesten verbreitet. Bei der Auswahl üblicher Kommunikationsnetze können Dörfer beispielsweise als Eckpunkte betrachtet werden. Wenn es einen Kommunikationspfad zwischen Dörfern gibt, wird dieser als Kante oder Bogen zwischen zwei Punkten betrachtet Kanten- oder Bogengewichtswert.
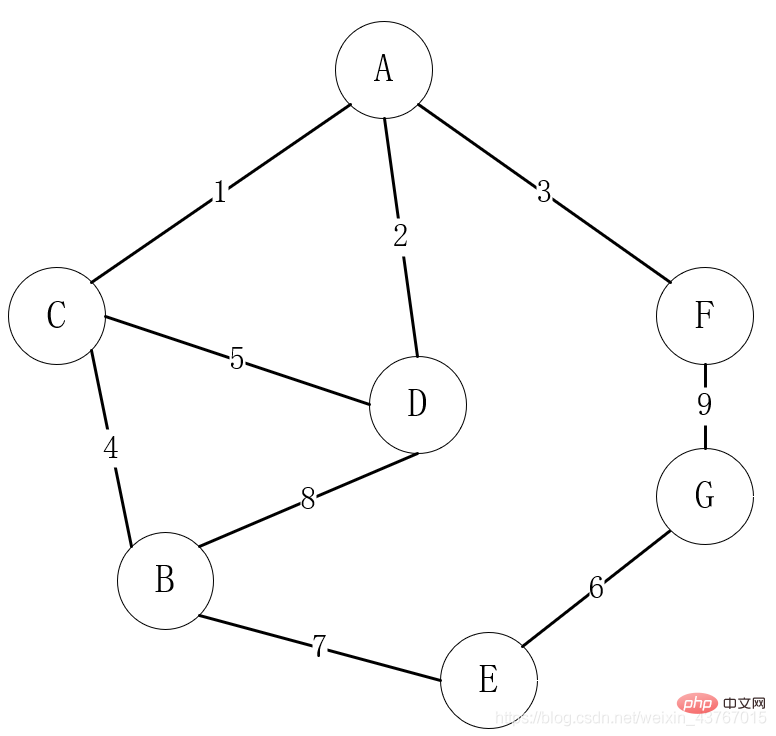
Das obige Bild zeigt einen Fall, in dem die Wahl der Route zum Aufbau eines Kommunikationsnetzwerks im Leben der Diagrammstruktur zugeordnet ist. Eckpunkte dienen als Dörfer. Wenn es Kommunikationswege zwischen Dörfern gibt, haben sie Kanten. Die Kosten für die Herstellung der Kommunikation zwischen Dörfern sind das Gewicht der Kanten.
Eine sehr häufige Anforderung ist, dass alle Dörfer, die kommunizieren können, kommunizieren müssen und die Kosten für den Kommunikationsaufbau minimal sind. Schließlich sind die Mittel „begrenzt“ und die Mittel gespart, hehe!
Das obige Problem, in ein mathematisches Modell umgewandelt, ist das Problem, den minimalen Spannbaum eines Diagramms zu finden, das heißt: Auswahl einer Route, die alle verbundenen Scheitelpunkte verbindet und die kleinste Summe der Gewichte aufweist. Es gibt viele Lösungen für dieses Problem. Die beiden klassischsten Algorithmen sind der Algorithmus von Prim und der Algorithmus von Kruskal.
2 Prims Algorithmus (Prim)
2.1 Prinzip
Prims Algorithmus beginnt an einem bestimmten Scheitelpunkt, unter der Annahme, dass alle Scheitelpunkte nicht verbunden sind, Finden Sie nach und nach die Kante mit dem geringsten Gewicht an jedem Scheitelpunkt, um sie zu verbinden und einen minimalen Spannbaum zu erstellen. Es verwendet Punkte als Ziel, um einen minimalen Spannbaum zu erstellen.
Die spezifischen Schritte sind: Wählen Sie zuerst zufällig einen Scheitelpunkt a aus, finden Sie, dass Scheitelpunkt a alle Scheitelpunkte verbinden kann, wählen Sie einen Scheitelpunkt mit einem geringen Gewicht zum Verbinden aus und suchen Sie dann einen Scheitelpunkt, der mit diesen beiden Scheitelpunkten verbunden ist oder kann verbunden werden Wählen Sie für alle Scheitelpunkte einen Scheitelpunkt mit einem geringen Gewicht aus, um ihn mit einem der Scheitelpunkte zu verbinden. Wiederholen Sie diesen Vorgang n-1-mal und wählen Sie dabei jedes Mal den Scheitelpunkt aus, der am kürzesten zu einem verbundenen Endscheitelpunkt liegt (anstelle des kürzesten Scheitelpunkts). erster Scheitelpunkt) zu verbinden, bis alle Scheitelpunkte verbunden sind und der minimale Spannbaum fertiggestellt ist.
2.2 Fallanalyse
Dieser Fall entspricht dem Fall im folgenden Implementierungscode.
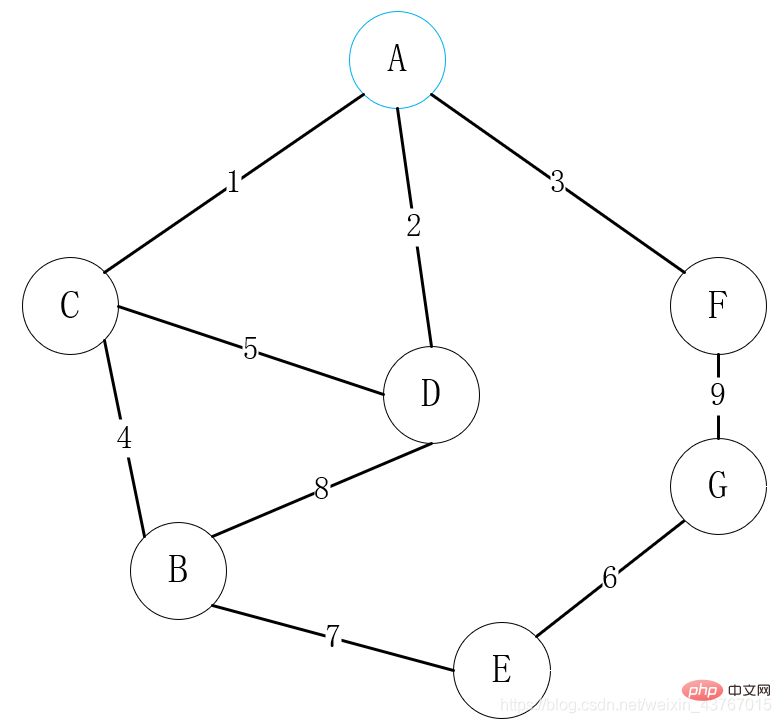
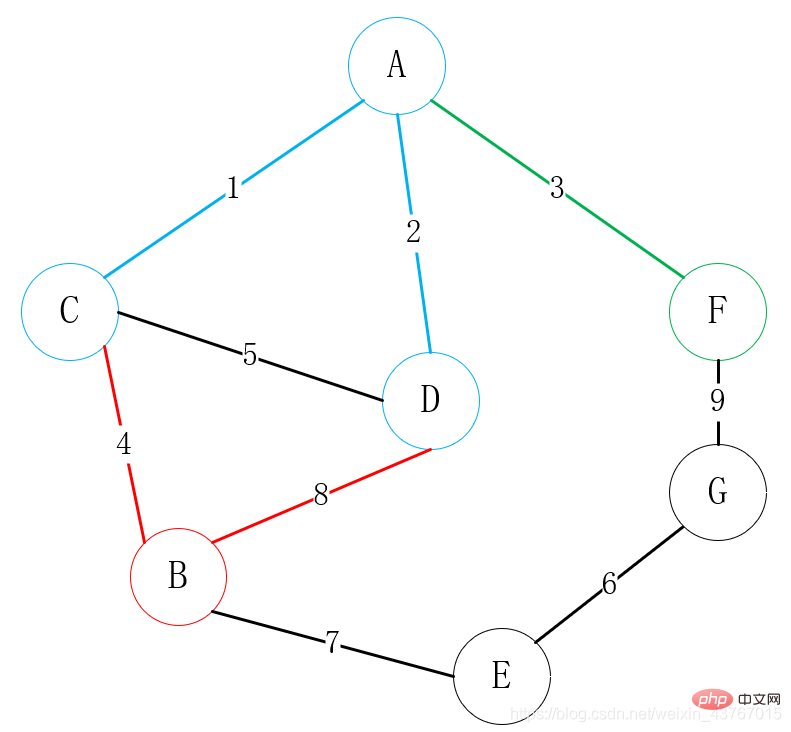
Wählen Sie in der obigen Abbildung zunächst Scheitelpunkt A als Verbindungspunkt aus, suchen Sie Scheitelpunkt A, um alle Scheitelpunkte C, D, F zu verbinden, und wählen Sie Scheitelpunkt A aus mit einem geringen Gewicht ist verbunden, hier wählen Sie A-C;
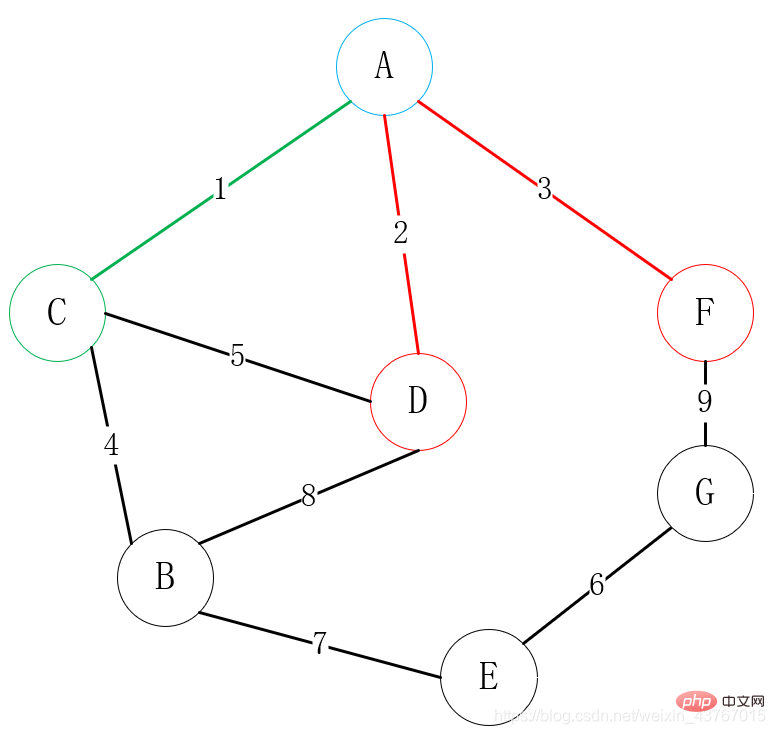
Suchen Sie dann alle Scheitelpunkte, die mit A oder C verbunden werden können (mit Ausnahme verbundener Punkte). B, D, F. Es stehen insgesamt 4 Kanten zur Auswahl: A-D, A-F, C-B, C-D. Wählen Sie einen Scheitelpunkt mit geringem Gewicht, um ihn mit einem der Scheitelpunkte zu verbinden 🎜## 🎜🎜#
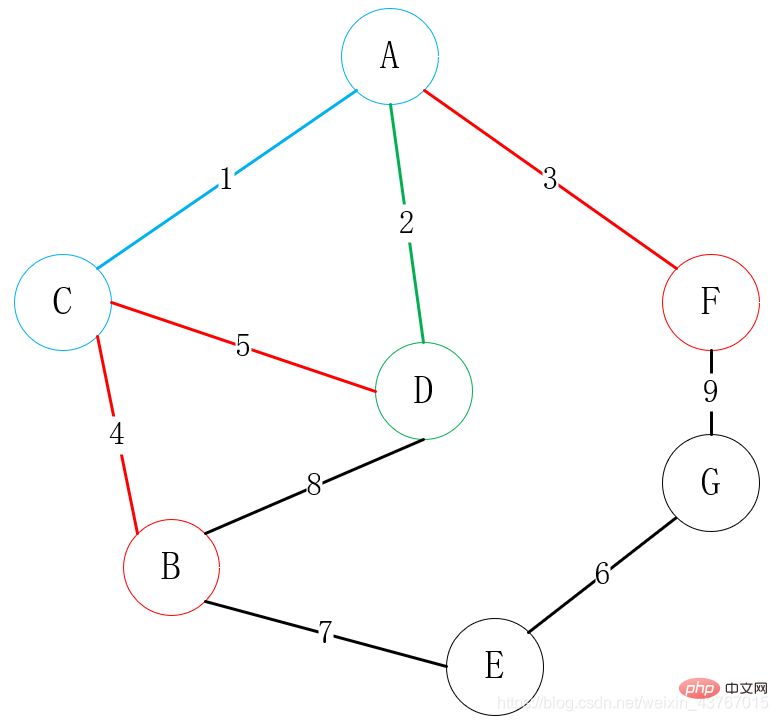Finden Sie dann alle Eckpunkte, die mit A, C oder D verbunden werden können (mit Ausnahme der verbundenen Punkte), suchen Sie B und F, es stehen 3 Kanten zur Auswahl , C-B, D-B, A-F, wählen Sie einen Scheitelpunkt mit geringem Gewicht, um ihn mit einem der Scheitelpunkte zu verbinden. Hier wählen wir offensichtlich A-F, um alle Scheitelpunkte zu verbinden, die mit C, D oder F verbunden werden können (mit Ausnahme der verbundenen Punkte). G, es stehen 3 Kanten zur Auswahl: C-B, D-B, F-G. Wählen Sie einen Scheitelpunkt mit geringem Gewicht, um ihn mit einem der Scheitelpunkte zu verbinden. Wählen Sie hier natürlich die C-B-Verbindung.
Finden Sie dann alle Scheitelpunkte, die mit A oder C oder D oder F oder B verbunden werden können (mit Ausnahme der verbundenen Punkte), finden Sie E, G, es stehen 2 Kanten zur Auswahl, B-E, F-G, wählen Sie einen Scheitelpunkt mit geringes Gewicht, um eine Verbindung mit einem der Scheitelpunkte herzustellen. Wählen Sie hier natürlich die B-E-Verbindung oder F oder B oder E (ohne verbundene Punkte), finde G, es stehen 2 Kanten zur Auswahl, E-G, F-G, wähle einen Scheitelpunkt mit geringem Gewicht aus, um ihn mit einem der Scheitelpunkte zu verbinden, hier wird offensichtlich die E-G-Verbindung ausgewählt; Der Spannbaum wurde mit einem Mindestgewicht von 23 konstruiert.
3 Kruskal-Algorithmus (Kruskal)
3.1 Prinzip
Kruskal-Algorithmus (Kruskal) wird schrittweise inkrementell entsprechend dem Gewicht des minimalen Spannbaums der Kante etabliert Ziel ist es, einen minimalen Spannbaum mit Kanten zu erstellen.
Die spezifischen Schritte sind: Behandeln Sie jeden Scheitelpunkt des gewichteten Diagramms als Wald, ordnen Sie dann die Gewichte jeder angrenzenden Kante im Diagramm in aufsteigender Reihenfolge an und beginnen Sie dann mit der Liste der angeordneten angrenzenden Kanten Kante mit dem kleinsten Gewicht, schreiben Sie den Startscheitelpunkt und den Endscheitelpunkt der Kante, verbinden Sie die Scheitelpunkte, um einen Wald zu einem Baum zu bilden, lesen Sie dann die angrenzenden Kanten der Start- und Endscheitelpunkte, extrahieren Sie zuerst die angrenzenden Kanten mit kleinen Gewichten und Verbinde die Eckpunkte weiter mit den Bäumen. Die Voraussetzung für das Hinzufügen benachbarter Kanten besteht darin, dass die dem Diagramm hinzugefügten benachbarten Kanten keinen Kreis (Ring) bilden. Dies wird wiederholt, bis n-1 Kanten hinzugefügt wurden. An diesem Punkt wird der minimale Spannbaum konstruiert.
3.2 Fallanalyse
Dieser Fall entspricht dem Fall im folgenden Implementierungscode:
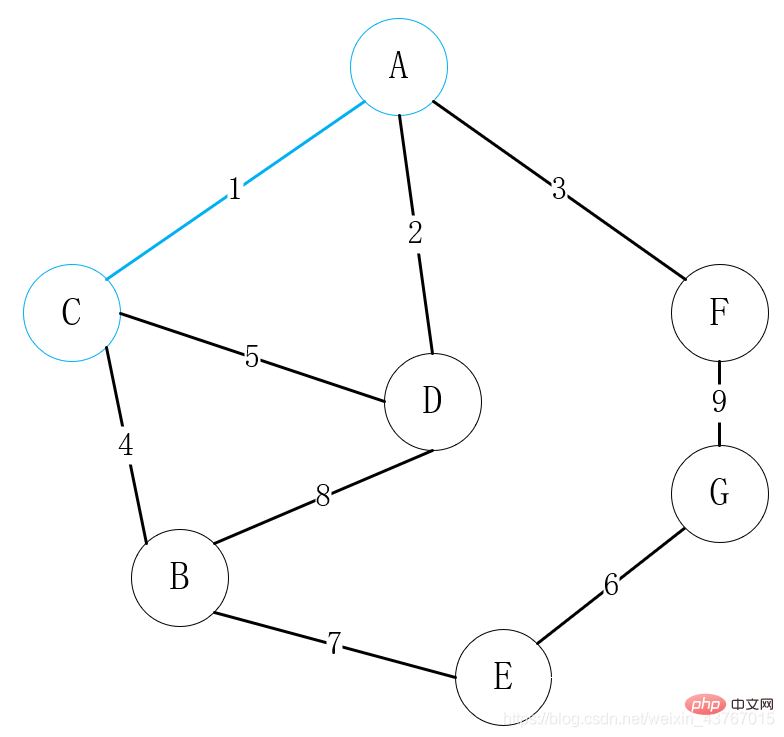
Zuerst erhalten Das Edge-Set-Array und Sortieren nach Gewicht von klein nach groß. Beim Sortieren im Code können Sie die Heap-Sortierung auch selbst implementieren. Die Ergebnisse nach dem Sortieren sind wie folgt.
Kante{von= A, bis=C, Gewicht=1}Kante{von=D, bis=A, Gewicht=2}Kante{von=A, bis=F, Gewicht=3}
Schleifen Sie die erste Kante A-C aus, stellen Sie fest, dass sie mit dem gefundenen minimalen Spannbaum keinen Zyklus bildet, und erhöhen Sie das Gesamtgewicht um 1 und fahren Sie fort; Gesamtgewicht um 2 und weiter; Erhöhen Sie das Gesamtgewicht um 3 und fahren Sie fort Baum, erhöhe das Gesamtgewicht um 4 und fahre fort; Baum, der gefunden wurde, verwerfen Sie diese Kante und fahren Sie fort; Finden Sie den minimalen Spannbaum, erhöhen Sie das Gesamtgewicht um 6 und fahren Sie fort Erhöhen Sie mit dem gefundenen minimalen Spannbaum das Gesamtgewicht um 7 und fahren Sie fort dass es eine Schleife mit dem gefundenen minimalen Spannbaum bildet. Stellen Sie fest, dass mit dem gefundenen minimalen Spannbaum eine Schleife gebildet wird, verwerfen Sie diese Kante und fahren Sie fort , dann wurde der minimale Spannbaum gefunden und das Gesamtgewicht des minimalen Spannbaums beträgt 23.
Kante{von=B, bis=C, Gewicht=4}
Kante{von=C, bis=D, Gewicht=5}
Kante{von=E, bis=G, Gewicht=6}
Kante{von=E, bis=B, Gewicht=7}
Kante{von=D, bis=B, Gewicht=8}
Kante{ von=F, bis=G, Gewicht=9}
In den obigen Schritten ist es wichtig zu bestimmen, ob ein Zyklus gebildet wird. Der übliche Ansatz besteht darin, die Eckpunkte des minimalen Spannbaums zu sortieren wurden gefunden (vom Startpunkt bis zum Endpunkt), und jedes Mal, wenn eine neue Kante hinzugefügt wird, werden der Startpunkt und der Endpunkt der neu hinzugefügten Kante verwendet, um den minimalen Binärbaum zu finden Der gefundene Endpunkt ist konsistent, was bedeutet, dass der minimale Spannbaum plus dieser Kante einen Zyklus bildet. Andernfalls bedeutet dies, dass der Endpunkt der Sortierung aktualisiert wird.
4 Adjazenzmatrix-gewichtete Diagrammimplementierung
Die Implementierung hier kann eine Klasse erstellen, die ein ungerichtetes gewichtetes Diagramm basierend auf der Adjazenzmatrix implementiert und Methoden für die Tiefendurchquerung bereitstellt Die Breiten-zuerst-Durchquerung bietet eine Methode zum Erhalten des Kantensatzarrays und zwei Methoden zum Ermitteln des minimalen Spannbaums: Prim und Kruskal.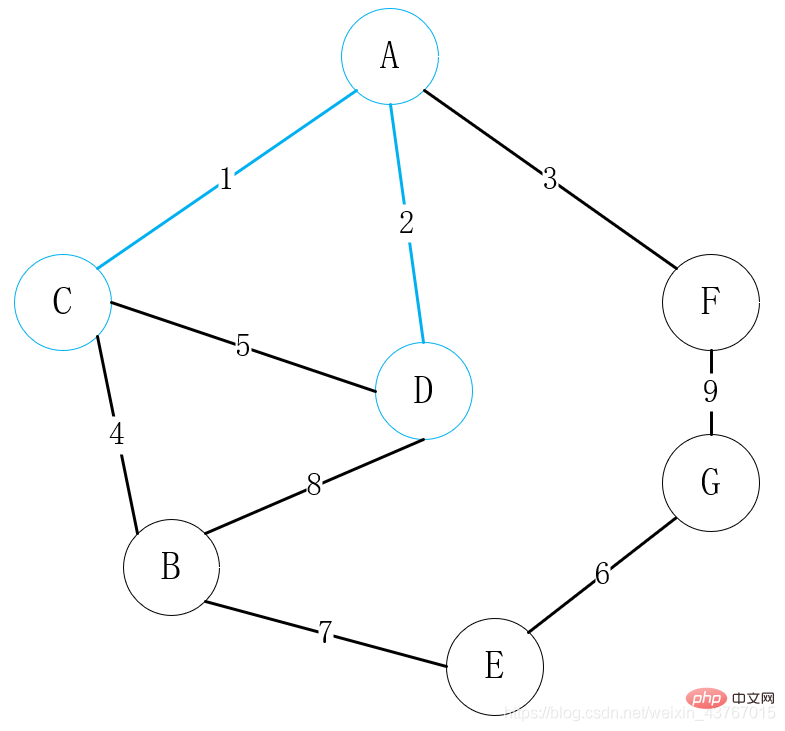 
/**
* 无向加权图邻接矩阵实现
* {@link MatrixPrimAndKruskal#MatrixPrimAndKruskal(E[], Edge[])} 构建无向加权图
* {@link MatrixPrimAndKruskal#DFS()} 深度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#BFS()} 广度优先遍历无向加权图
* {@link MatrixPrimAndKruskal#toString()} 输出无向加权图
* {@link MatrixPrimAndKruskal#prim()} Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskal()} Kruskal算法实现最小生成树
* {@link MatrixPrimAndKruskal#kruskalAndPrim()} Kruskal算法结合Prim算法实现最小生成树
* {@link MatrixPrimAndKruskal#getEdges()} 获取边集数组
*
* @author lx
* @date 2020/5/14 18:13
*/
public class MatrixPrimAndKruskal<E> {
/**
* 顶点数组
*/
private Object[] vertexs;
/**
* 邻接矩阵
*/
private int[][] matrix;
/**
*
*/
private Edge<E>[] edges;
/**
* 由于是加权图,这里设置一个边的权值上限,任何边的最大权值不能大于等于该值，在实际应用中，该值应该根据实际情况确定
*/
private static final int NO_EDGE = 99;
/**
* 边对象,具有权值,在构建加权无向图时使用
*/
private static class Edge<E> {
private E from;
private E to;
private int weight;
public Edge(E from, E to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
/**
* 创建无向加权图
*
* @param vertexs 顶点数组
* @param edges 边对象数组
*/
public MatrixPrimAndKruskal(Object[] vertexs, Edge<E>[] edges) {
//初始化边数组
this.edges = edges;
// 初始化顶点数组,并添加顶点
this.vertexs = Arrays.copyOf(vertexs, vertexs.length);
// 初始化边矩阵,并预先填充边信息
this.matrix = new int[vertexs.length][vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
if (i == j) {
this.matrix[i][j] = 0;
} else {
this.matrix[i][j] = NO_EDGE;
}
}
}
for (Edge<E> edge : edges) {
// 读取一条边的起始顶点和结束顶点索引值
int p1 = getPosition(edge.from);
int p2 = getPosition(edge.to);
//对称的两个点位都置为edge.weight,无向图可以看作相互可达的有向图
this.matrix[p1][p2] = edge.weight;
this.matrix[p2][p1] = edge.weight;
}
}
/**
* 获取某条边的某个顶点所在顶点数组的索引位置
*
* @param e 顶点的值
* @return 所在顶点数组的索引位置, 或者-1 - 表示不存在
*/
private int getPosition(E e) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == e) {
return i;
}
}
return -1;
}
/**
* 深度优先搜索遍历图,类似于树的前序遍历,
*/
public void DFS() {
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
//初始化所有顶点都没有被访问
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("DFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
DFS(i, visited);
}
}
System.out.println();
}
/**
* 深度优先搜索遍历图的递归实现,类似于树的先序遍历
* 因此模仿树的先序遍历,同样借用栈结构,这里使用的是方法的递归,隐式的借用栈
*
* @param i 顶点索引
* @param visited 访问标志数组
*/
private void DFS(int i, boolean[] visited) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
// 遍历该顶点的所有邻接点。若该邻接点是没有访问过，那么继续递归遍历领接点
for (int w = firstVertex(i); w >= 0; w = nextVertex(i, w)) {
if (!visited[w]) {
DFS(w, visited);
}
}
}
/**
* 广度优先搜索图,类似于树的层序遍历
* 因此模仿树的层序遍历,同样借用队列结构
*/
public void BFS() {
// 辅组队列
Queue<Integer> indexLinkedList = new LinkedList<>();
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("BFS: ");
for (int i = 0; i < vertexs.length; i++) {
if (!visited[i]) {
visited[i] = true;
System.out.print(vertexs[i] + " ");
indexLinkedList.add(i);
}
if (!indexLinkedList.isEmpty()) {
//j索引出队列
Integer j = indexLinkedList.poll();
//继续访问j的邻接点
for (int k = firstVertex(j); k >= 0; k = nextVertex(j, k)) {
if (!visited[k]) {
visited[k] = true;
System.out.print(vertexs[k] + " ");
//继续入队列
indexLinkedList.add(k);
}
}
}
}
System.out.println();
}
/**
* 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*
* @param v 顶点v在数组中的索引
* @return 返回顶点v的第一个邻接顶点的索引，失败则返回-1
*/
private int firstVertex(int v) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 从i=0开始*/
for (int i = 0; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*
* @param v 顶点索引
* @param w 第一个邻接点索引
* @return 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
*/
private int nextVertex(int v, int w) {
//如果索引超出范围,则返回-1
if (v < 0 || v > (vertexs.length - 1) || w < 0 || w > (vertexs.length - 1)) {
return -1;
}
/*根据邻接矩阵的规律:顶点索引v对应着边二维矩阵的matrix[v][i]一行记录
* 由于邻接点w的索引已经获取了,所以从i=w+1开始寻找*/
for (int i = w + 1; i < vertexs.length; i++) {
if (matrix[v][i] != 0 && matrix[v][i] != NO_EDGE) {
return i;
}
}
return -1;
}
/**
* 输出图
*
* @return 输出图字符串
*/
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < vertexs.length; i++) {
for (int j = 0; j < vertexs.length; j++) {
stringBuilder.append(matrix[i][j]).append("\t");
}
stringBuilder.append("\n");
}
return stringBuilder.toString();
}
/**
* Prim算法求最小生成树
*/
public void prim() {
System.out.println("prim: ");
//对应节点应该被连接的前驱节点,用来输出
//默认为0,即前驱结点为第一个节点
int[] mid = new int[matrix.length];
//如果某顶点作为末端顶点被连接，对应位置应该为true
//第一个顶点默认被连接
boolean[] connected = new boolean[matrix.length];
connected[0] = true;
//存储未连接顶点到已连接顶点的最短距离(最小权)
int[] dis = new int[matrix.length];
//首先将矩阵第一行即其他顶点到0索引顶点的权值拷贝进去
System.arraycopy(matrix[0], 0, dis, 0, matrix.length);
//存储路径长度
int sum = 0;
//最小权值
int min;
/*默认第一个顶点已经找到了,因此最多还要需要大循环n-1次*/
for (int k = 1; k < matrix.length; k++) {
min = NO_EDGE;
//最小权值的顶点的索引
int minIndex = 0;
/*寻找权值最小的且未被连接的顶点索引*/
for (int i = 1; i < matrix.length; i++) {
//排除已连接的顶点,排除权值等于0的值,这里权值等于0表示已生成的最小生成树的顶点都未能与该顶点连接
if (!connected[i] && dis[i] != 0 && dis[i] < min) {
min = dis[i];
minIndex = i;
}
}
//如果没找到,那么该图可能不是连通图,直接返回了,此时最小生成树没啥意义
if (minIndex == 0) {
return;
}
//权值和增加
sum += min;
//该新连接顶点对应的索引值变成true,表示已被连接,后续判断时跳过该顶点
connected[minIndex] = true;
//输出对应的前驱顶点到该最小顶点的权值
System.out.println(vertexs[mid[minIndex]] + " ---> " + vertexs[minIndex] + " 权值:" + min);
/*在新顶点minIndex加入之前的其他所有顶点到连接顶点最小的权值已经计算过了
因此只需要更新其他未连接顶点到新连接顶点minIndex是否还有更短的权值,有的话就更新找到距离已连接的顶点权最小的顶点*/
for (int i = 1; i < matrix.length; i++) {
//如果该顶点未连接
if (!connected[i]) {
/*如果新顶点到未连接顶点i的权值不为0,并且比原始顶点到未连接顶点i的权值还要小,那么更新对应位置的最小权值*/
if (matrix[minIndex][i] != 0 && dis[i] > matrix[minIndex][i]) {
//更新最小权值
dis[i] = matrix[minIndex][i];
//更新前驱节点索引为新加入节点索引
mid[i] = minIndex;
}
}
}
}
System.out.println("sum: " + sum);
}
/**
* Kruskal算法求最小生成树传统实现,要求知道边集数组,和顶点数组
*/
public void kruskal() {
System.out.println("Kruskal: ");
//由于创建图的时候保存了边集数组,这里直接使用就行了
//Edge[] edges = getEdges();
//this.edges=edges;
//对边集数组进行排序
Arrays.sort(this.edges, Comparator.comparingInt(o -> o.weight));
// 用于保存已有最小生成树中每个顶点在该最小树中的最终终点的索引
int[] vends = new int[this.edges.length];
//能够知道终点索引范围是[0,this.edges.length-1],因此填充edges.length表示没有终点
Arrays.fill(vends, this.edges.length);
int sum = 0;
for (Edge<E> edge : this.edges) {
// 获取第i条边的起点索引from
int from = getPosition(edge.from);
// 获取第i条边的终点索引to
int to = getPosition(edge.to);
// 获取顶点from在"已有的最小生成树"中的终点
int m = getEndIndex(vends, from);
// 获取顶点to在"已有的最小生成树"中的终点
int n = getEndIndex(vends, to);
// 如果m!=n，意味着没有形成环路,则可以添加,否则直接跳过,进行下一条边的判断
if (m != n) {
//添加设置原始终点索引m在已有的最小生成树中的终点为n
vends[m] = n;
System.out.println(vertexs[from] + " ---> " + vertexs[to] + " 权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("sum: " + sum);
//System.out.println(Arrays.toString(this.edges));
}
/**
* 获取顶点索引i的终点如果没有终点则返回顶点索引本身
*
* @param vends 顶点在最小生成树中的终点
* @param i 顶点索引
* @return 顶点索引i的终点如果没有终点则返回顶点索引本身
*/
private int getEndIndex(int[] vends, int i) {
//这里使用循环查找的逻辑,寻找的是最终的终点
while (vends[i] != this.edges.length) {
i = vends[i];
}
return i;
}
/**
* 如果没有现成的边集数组，那么根据邻接矩阵结构获取图中的边集数组
*
* @return 图的边集数组
*/
private Edge[] getEdges() {
List<Edge> edges = new ArrayList<>();
/*遍历矩阵数组 只需要遍历一半就行了*/
for (int i = 0; i < vertexs.length; i++) {
for (int j = i + 1; j < vertexs.length; j++) {
//如果存在边
if (matrix[i][j] != NO_EDGE && matrix[i][j] != 0) {
edges.add(new Edge<>(vertexs[i], vertexs[j], matrix[i][j]));
//edges[index++] = new Edge(vertexs[i], vertexs[j], matrix[i][j]);
}
}
}
return edges.toArray(new Edge[0]);
}
/**
* Kruskal结合Prim算法.不需要知道边集,只需要矩阵数组,和顶点数组
* 同样是求最小权值的边,但是有一个默认起点顶点,该起点可以是要求[0,顶点数量-1]之间的任意值，同时查找最小权的边。
* 可能会有Bug,目前未发现
*/
public void kruskalAndPrim() {
System.out.println("kruskalAndPrim: ");
//已经找到的边携带的顶点对应的索引将变为true,其余未找到边对应的顶点将是false
boolean[] connected = new boolean[matrix.length];
//这里选择第一个顶点为起点,表示以该顶点开始寻找包含该顶点的最小边
connected[0] = true;
int sum = 0, n1 = 0, n2 = 0;
//最小权值
int min;
while (true) {
min = NO_EDGE;
/*找出所有带有已找到顶点的边中,最小权值的边,只需要寻找对称矩阵的一半即可*/
//第一维
for (int i = 0; i < matrix.length; i++) {
//第二维
for (int j = i + 1; j < matrix.length; j++) {
//排除等于0的,排除两个顶点都找到了的,这里实际上已经隐含了排除环的逻辑,如果某条边的两个顶点都找到了,那么如果算上该条边,肯定会形成环
//寻找剩下的最小的权值的边
if (matrix[i][j] != 0 && connected[i] != connected[j] && matrix[i][j] < min) {
min = matrix[i][j];
n1 = i;
n2 = j;
}
}
}
//如果没找到最小权值,该图可能不是连通图,或者已经寻找完毕,直接返回
if (min == NO_EDGE) {
System.out.println(" sum:" + sum);
return;
}
//已经找到的边对应的两个顶点都置为true
connected[n1] = true;
connected[n2] = true;
//输出找到的边和最小权值
System.out.println(vertexs[n1] + " ---> " + vertexs[n2] + " 权值:" + min);
sum += min;
}
}
public static void main(String[] args) {
//顶点数组
Character[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//边数组,加权值
Edge[] edges = {
new Edge<>('A', 'C', 1),
new Edge<>('D', 'A', 2),
new Edge<>('A', 'F', 3),
new Edge<>('B', 'C', 4),
new Edge<>('C', 'D', 5),
new Edge<>('E', 'G', 6),
new Edge<>('E', 'B', 7),
new Edge<>('D', 'B', 8),
new Edge<>('F', 'G', 9)};
//构建图
MatrixPrimAndKruskal<Character> matrixPrimAndKruskal = new MatrixPrimAndKruskal<Character>(vexs, edges);
//输出图
System.out.println(matrixPrimAndKruskal);
//深度优先遍历
matrixPrimAndKruskal.DFS();
//广度优先遍历
matrixPrimAndKruskal.BFS();
//Prim算法输出最小生成树
matrixPrimAndKruskal.prim();
//Kruskal算法输出最小生成树
matrixPrimAndKruskal.kruskal();
//Kruskal算法结合Prim算法输出最小生成树,可能会有Bug,目前未发现
matrixPrimAndKruskal.kruskalAndPrim();
//获取边集数组
Edge[] edges1 = matrixPrimAndKruskal.getEdges();
System.out.println(Arrays.toString(edges1));
}
}5 Adjazenzlisten-gewichtete GraphenimplementierungDie Implementierung hier kann eine Klasse erstellen, die einen ungerichteten gewichteten Graphen basierend auf der Adjazenzliste implementiert; -first traversal Methode, stellt eine Methode zum Erhalten des Kantensatzarrays bereit und bietet zwei Methoden zum Ermitteln des minimalen Spannbaums: Prim und Kruskal. /**
* 无向加权图邻接表实现
* {@link ListPrimAndKruskal#ListPrimAndKruskal(E[], Edge[])} 构建无向加权图
* {@link ListPrimAndKruskal#DFS()} 深度优先遍历无向加权图
* {@link ListPrimAndKruskal#BFS()} 广度优先遍历无向加权图
* {@link ListPrimAndKruskal#toString()} 输出无向加权图
* {@link ListPrimAndKruskal#prim()} Prim算法实现最小生成树
* {@link ListPrimAndKruskal#kruskal()} Kruskal算法实现最小生成树
* {@link ListPrimAndKruskal#getEdges()} 获取边集数组
*
* @author lx
* @date 2020/5/14 23:31
*/
public class ListPrimAndKruskal<E> {
/**
* 顶点类
*
* @param <E>
*/
private class Node<E> {
/**
* 顶点信息
*/
E data;
/**
* 指向第一条依附该顶点的边
*/
LNode firstLNode;
public Node(E data, LNode firstLNode) {
this.data = data;
this.firstLNode = firstLNode;
}
}
/**
* 边表节点类
*/
private class LNode {
/**
* 该边所指向的顶点的索引位置
*/
int vertex;
/**
* 该边的权值
*/
int weight;
/**
* 指向下一条边的指针
*/
LNode nextLNode;
}
/**
* 边对象,具有权值,在构建加权无向图时使用
*/
private static class Edge<E> {
private E from;
private E to;
private int weight;
public Edge(E from, E to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge{" +
"from=" + from +
", to=" + to +
", weight=" + weight +
'}';
}
}
/**
* 顶点数组
*/
private Node<E>[] vertexs;
/**
* 边数组
*/
private Edge<E>[] edges;
/**
* 由于是加权图,这里设置一个边的权值上限,任何边的最大权值不能大于等于该值，在实际应用中，该值应该根据实际情况确定
*/
private static final int NO_EDGE = 99;
/**
* 创建无向加权图
*
* @param vexs 顶点数组
* @param edges 边二维数组
*/
public ListPrimAndKruskal(E[] vexs, Edge<E>[] edges) {
this.edges = edges;
/*初始化顶点数组,并添加顶点*/
vertexs = new Node[vexs.length];
for (int i = 0; i < vertexs.length; i++) {
vertexs[i] = new Node<>(vexs[i], null);
}
/*初始化边表,并添加边节点到边表尾部,即采用尾插法*/
for (Edge<E> edge : edges) {
// 读取一条边的起始顶点和结束顶点索引值
int p1 = getPosition(edge.from);
int p2 = getPosition(edge.to);
int weight = edge.weight;
/*这里需要相互添加边节点,无向图可以看作相互可达的有向图*/
// 初始化lnode1边节点
LNode lnode1 = new LNode();
lnode1.vertex = p2;
lnode1.weight = weight;
// 将LNode链接到"p1所在链表的末尾"
if (vertexs[p1].firstLNode == null) {
vertexs[p1].firstLNode = lnode1;
} else {
linkLast(vertexs[p1].firstLNode, lnode1);
}
// 初始化lnode2边节点
LNode lnode2 = new LNode();
lnode2.vertex = p1;
lnode2.weight = weight;
// 将lnode2链接到"p2所在链表的末尾"
if (vertexs[p2].firstLNode == null) {
vertexs[p2].firstLNode = lnode2;
} else {
linkLast(vertexs[p2].firstLNode, lnode2);
}
}
}
/**
* 获取某条边的某个顶点所在顶点数组的索引位置
*
* @param e 顶点的值
* @return 所在顶点数组的索引位置, 或者-1 - 表示不存在
*/
private int getPosition(E e) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i].data == e) {
return i;
}
}
return -1;
}
/**
* 将lnode节点链接到边表的最后,采用尾插法
*
* @param first 边表头结点
* @param node 将要添加的节点
*/
private void linkLast(LNode first, LNode node) {
while (true) {
if (first.vertex == node.vertex) {
return;
}
if (first.nextLNode == null) {
break;
}
first = first.nextLNode;
}
first.nextLNode = node;
}
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
for (int i = 0; i < vertexs.length; i++) {
stringBuilder.append(i).append("(").append(vertexs[i].data).append("): ");
LNode node = vertexs[i].firstLNode;
while (node != null) {
stringBuilder.append(node.vertex).append("(").append(vertexs[node.vertex].data).append("-").append(node.weight).append(")");
node = node.nextLNode;
if (node != null) {
stringBuilder.append("->");
} else {
break;
}
}
stringBuilder.append("\n");
}
return stringBuilder.toString();
}
/**
* 深度优先搜索遍历图的递归实现,类似于树的先序遍历
* 因此模仿树的先序遍历,同样借用栈结构,这里使用的是方法的递归,隐式的借用栈
*
* @param i 顶点索引
* @param visited 访问标志数组
*/
private void DFS(int i, boolean[] visited) {
//索引索引标记为true ,表示已经访问了
visited[i] = true;
System.out.print(vertexs[i].data + " ");
//获取该顶点的边表头结点
LNode node = vertexs[i].firstLNode;
//循环遍历该顶点的邻接点,采用同样的方式递归搜索
while (node != null) {
if (!visited[node.vertex]) {
DFS(node.vertex, visited);
}
node = node.nextLNode;
}
}
/**
* 深度优先搜索遍历图,类似于树的前序遍历,
*/
public void DFS() {
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
//初始化所有顶点都没有被访问
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("DFS: ");
/*循环搜索*/
for (int i = 0; i < vertexs.length; i++) {
//如果对应索引的顶点的访问标记为false,则搜索该顶点
if (!visited[i]) {
DFS(i, visited);
}
}
/*走到这一步,说明顶点访问标记数组全部为true,说明全部都访问到了,深度搜索结束*/
System.out.println();
}
/**
* 广度优先搜索图,类似于树的层序遍历
* 因此模仿树的层序遍历,同样借用队列结构
*/
public void BFS() {
// 辅组队列
Queue<Integer> indexLinkedList = new LinkedList<>();
//新建顶点访问标记数组,对应每个索引对应相同索引的顶点数组中的顶点
boolean[] visited = new boolean[vertexs.length];
//初始化所有顶点都没有被访问
for (int i = 0; i < vertexs.length; i++) {
visited[i] = false;
}
System.out.println("BFS: ");
for (int i = 0; i < vertexs.length; i++) {
//如果访问方剂为false,则设置为true,表示已经访问,然后开始访问
if (!visited[i]) {
visited[i] = true;
System.out.print(vertexs[i].data + " ");
indexLinkedList.add(i);
}
//判断队列是否有值,有就开始遍历
if (!indexLinkedList.isEmpty()) {
//出队列
Integer j = indexLinkedList.poll();
LNode node = vertexs[j].firstLNode;
while (node != null) {
int k = node.vertex;
if (!visited[k]) {
visited[k] = true;
System.out.print(vertexs[k].data + " ");
//继续入队列
indexLinkedList.add(k);
}
node = node.nextLNode;
}
}
}
System.out.println();
}
/**
* Prim算法求最小生成树
*/
public void prim() {
System.out.println("prim: ");
//对应节点应该被连接的前驱节点,用来输出
//默认为0,即前驱结点为第一个节点
int[] mid = new int[vertexs.length];
int start = 0;
int min, tmp, sum = 0;
int num = vertexs.length;
//顶点间边的权值
//存储未连接顶点到已连接顶点的最短距离(最小权)
int[] dis = new int[num];
// 初始化"顶点的权值数组"，
// 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
//首先将其他顶点到0索引顶点的权值存储进去
for (int i = 0; i < num; i++) {
dis[i] = getWeight(start, i);
}
//如果某顶点作为末端顶点被连接，对应位置应该为true
//第一个顶点默认被连接
boolean[] connected = new boolean[vertexs.length];
connected[0] = true;
/*默认第一个顶点已经找到了,因此最多还要需要大循环n-1次*/
for (int k = 1; k < num; k++) {
min = NO_EDGE;
//最小权值的顶点的索引
int minIndex = 0;
// 在未被加入到最小生成树的顶点中，找出权值最小的顶点。
for (int i = 1; i < vertexs.length; i++) {
//排除已连接的顶点,排除权值等于0的值,因为这里默认顶点指向自己的权值为0
if (!connected[i] && dis[i] != 0 && dis[i] < min) {
min = dis[i];
minIndex = i;
}
}
//如果没找到,那么该图可能不是连通图,直接返回了,此时最小生成树没啥意义
if (minIndex == 0) {
return;
}
//权值和增加
sum += min;
//该新连接顶点对应的索引值变成true,表示已被连接,后续判断时跳过该顶点
connected[minIndex] = true;
//输出对应的前驱顶点到该最小顶点的权值
System.out.println(vertexs[mid[minIndex]].data + " ---> " + vertexs[minIndex].data + " 权值:" + min);
/*在新顶点minIndex加入之前的其他所有顶点到连接顶点最小的权值已经计算过了
因此只需要更新其他顶点到新连接顶点minIndex是否还有更短的权值,有的话就更新找到距离已连接的顶点权最小的顶点*/
for (int i = 1; i < num; i++) {
//如果该顶点未连接
if (!connected[i]) {
// 获取minindex顶点到未连接顶点i的权值
tmp = getWeight(minIndex, i);
/*如果新顶点到未连接顶点i的权值不为0,并且比原始顶点到未连接顶点i的权值还要小,那么更新对应位置的最小权值*/
if (tmp != 0 && dis[i] > tmp) {
dis[i] = tmp;
//更新前驱节点索引为新加入节点索引
mid[i] = minIndex;
}
}
}
}
System.out.println("sum: " + sum);
}
/**
* 尝试获取边起点start到边终点end的边的权值,当然可能获取不到
*
* @param start 边起点
* @param end 边终点
* @return 返回权值; 如果起点和终点相同则返回0;如果边起点和边终点之间并没有边, 则返回NO_EDGE
*/
private int getWeight(int start, int end) {
//如果start=end，则返回0
if (start == end) {
return 0;
}
//获取该顶点的边表的第一个值
LNode node = vertexs[start].firstLNode;
//循环查找边表,看能否找到对应的索引=end,找不到就返回NO_EDGE,表示两个顶点未连接。
while (node != null) {
if (end == node.vertex) {
return node.weight;
}
node = node.nextLNode;
}
return NO_EDGE;
}
/**
* Kruskal算法求最小生成树,可以说邻接矩阵和邻接链表的实现方式是完全一致的
*/
public void kruskal() {
//由于创建图的时候保存了边集数组,这里直接使用就行了
//Edge[] edges = getEdges();
//this.edges=edges;
//对边集数组进行排序
Arrays.sort(this.edges, Comparator.comparingInt(o -> o.weight));
// 用于保存已有最小生成树中每个顶点在该最小树中的最终终点的索引
int[] vends = new int[this.edges.length];
//能够知道终点索引范围是[0,this.edges.length-1],因此填充edges.length表示没有终点
Arrays.fill(vends, this.edges.length);
int sum = 0;
for (Edge<E> edge : this.edges) {
// 获取第i条边的起点索引from
int from = getPosition(edge.from);
// 获取第i条边的终点索引to
int to = getPosition(edge.to);
// 获取顶点from在"已有的最小生成树"中的终点
int m = getEndIndex(vends, from);
// 获取顶点to在"已有的最小生成树"中的终点
int n = getEndIndex(vends, to);
// 如果m!=n，意味着没有形成环路,则可以添加,否则直接跳过,进行下一条边的判断
if (m != n) {
//添加设置原始终点索引m在已有的最小生成树中的终点为n
vends[m] = n;
System.out.println(vertexs[from].data + " ---> " + vertexs[to].data + " 权值:" + edge.weight);
sum += edge.weight;
}
}
System.out.println("sum: " + sum);
//System.out.println(Arrays.toString(this.edges));
}
/**
* 获取顶点索引i的终点如果没有终点则返回顶点索引本身
*
* @param vends 顶点在最小生成树中的终点
* @param i 顶点索引
* @return 顶点索引i的终点如果没有终点则返回顶点索引本身
*/
private int getEndIndex(int[] vends, int i) {
//这里使用循环查找的逻辑,寻找的是最终的终点
while (vends[i] != this.edges.length) {
i = vends[i];
}
return i;
}
/**
* 如果没有现成的边集数组，那么根据邻接表结构获取图中的边集数组
*
* @return 图的边集数组
*/
private Edge[] getEdges() {
List<Edge> edges = new ArrayList<>();
//遍历顶点数组
for (int i = 0; i < vertexs.length; i++) {
LNode node = vertexs[i].firstLNode;
while (node != null) {
//只需添加起点索引小于终点索引的边就行了
if (node.vertex > i) {
edges.add(new Edge<>(vertexs[i].data, vertexs[node.vertex].data, node.weight));
}
node = node.nextLNode;
}
}
return edges.toArray(new Edge[0]);
}
public static void main(String[] args) {
//顶点数组
Character[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//边数组,加权值
Edge[] edges = {
new Edge('A', 'C', 1),
new Edge('D', 'A', 2),
new Edge('A', 'F', 3),
new Edge('B', 'C', 4),
new Edge('C', 'D', 5),
new Edge('E', 'G', 6),
new Edge('E', 'B', 7),
new Edge('D', 'B', 8),
new Edge('F', 'G', 9)};
//构建图
ListPrimAndKruskal<Character> listPrimAndKruskal = new ListPrimAndKruskal<Character>(vexs, edges);
//输出图
System.out.println(listPrimAndKruskal);
//深度优先遍历
//DFS:
//A C B E G F D
listPrimAndKruskal.DFS();
//广度优先遍历
//BFS:
//A C D F B G E
listPrimAndKruskal.BFS();
//Prim算法求最小生成树
listPrimAndKruskal.prim();
//Kruskal算法求最小生成树
listPrimAndKruskal.kruskal();
//获取边集数组
Edge[] edges1 = listPrimAndKruskal.getEdges();
System.out.println(Arrays.toString(edges1));
}
}Das obige ist der detaillierte Inhalt vonSo finden Sie den minimalen Spanning Tree in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!