Heim >Java >javaLernprogramm >Welche Techniken gibt es für Java-Bit-Operationen?
Welche Techniken gibt es für Java-Bit-Operationen?
- PHPznach vorne
- 2023-04-29 10:34:061686Durchsuche
Was ist eine Bitoperation? Bei der Datenmethode auf Binärebene verarbeitet die Bitoperation direkt Binärdaten, die aus 0 und 1 bestehen.
Grundlegende Bitoperationen
Es gibt sechs grundlegende Bitoperationen, nämlich** AND oder NOT XOR Linksverschiebung Rechtsverschiebung* *#🎜🎜 #
Symbol| Bedienungsregeln | # 🎜🎜## 🎜🎜# | & |
|---|---|---|
| oder | Wenn beide Bits 0 sind, ist das Ergebnis 0 | |
| XOR | Wenn die beiden Bits gleich sind, ist das Ergebnis 1, wenn sie nicht gleich sind, ist das Ergebnis 0 | #🎜 🎜# | ~
| 0 ändert sich zu 1, 1 ändert sich zu 0 | # 🎜🎜# | |
Nachfolgend analysieren wir, warum dieses Ergebnis ausgegeben wird:
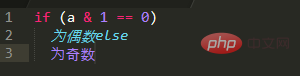
Bitoperationen werden häufig für einige kleine Operationen verwendet, da sie nur plastische Zahlen verarbeiten können, sodass ihre Einsatzmöglichkeiten begrenzt sind. Es lohnt sich jedoch, einige häufig verwendete Tipps zu beherrschen, z. B. die Beurteilung von geraden und ungeraden Zahlen, den Austausch zweier Zahlen, den Austausch von Vorzeichen und das Ermitteln absoluter Werte , usw. Wir werden sie im Folgenden einzeln vorstellen. #? Ende ist 0, es ist eine gerade Zahl. Wenn die letzte Ziffer 1 ist, ist es eine ungerade Zahl. Der Weg zur Bestimmung der Parität ist also:Ein kleines Testprogramm:# 🎜🎜#Das obige Programm gibt alle geraden Zahlen innerhalb von 1000 aus.Austausch von zwei Zahlen
(a b). Da die-Operation das Kommutativgesetz erfüllt, b( ab)=bb^a. Eine Zahl, die mit sich selbst XOR-verknüpft wird, muss 0 sein, denn wenn eine Zahl mit 0 XOR-verknüpft wird, sind 1 und 0 immer noch 1, und 0 und 0 sind immer noch 0, also offensichtlich eine Zahl und 0 Nach XOR ist es natürlich immer noch es selbst. Zu diesem Zeitpunkt wird b also der Wert a zugewiesen.Der letzte Schritt, a^=b ist a=a b, da die beiden vorherigen Schritte zeigen, dass a=(ab), b=a, also a=a
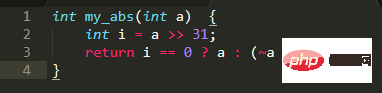
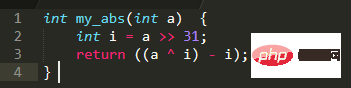
Um das Positive oder Negative zu bestimmen, können Sie das Vorzeichenbit direkt bestimmen, 31 Bits nach rechts verschieben, das Vorzeichenbit erhalten und das Positive oder Negative bestimmen# 🎜🎜#Für jede Zahl bleibt XOR mit 0 unverändert, XOR mit -1, also 0xFFFFFFFF, entspricht einer Negation. Daher kann der Absolutwert auch durch XOR-Verknüpfung von a mit i und anschließendes Subtrahieren von i erhalten werden (da i 0 oder -1 ist, bedeutet das Subtrahieren von i also entweder das Addieren von 0 oder das Addieren von 1). So können Sie den obigen Code optimieren:
Anwendung von Bitoperationen#🎜 🎜#Häufige Algorithmusfragen. Bitoperationen zur Implementierung von A+B-Operationen sind häufige Algorithmusfragen.
Lassen Sie uns nun das Prinzip der Bitoperation erklären, um die Addition zweier Zahlen zu implementieren. Zum Beispiel b : 0110#🎜🎜 #Keine Übertragssumme: 0101 Das ist 5 Übertrag: 0010 Das ist 2 Also wird a+b zu 5 + (25 0101
|
Das obige ist der detaillierte Inhalt vonWelche Techniken gibt es für Java-Bit-Operationen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!


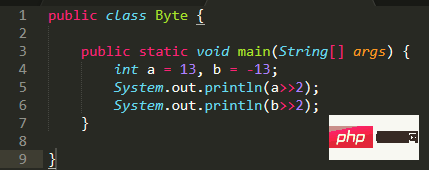 Die Ausgabe des obigen Codes:
Die Ausgabe des obigen Codes: 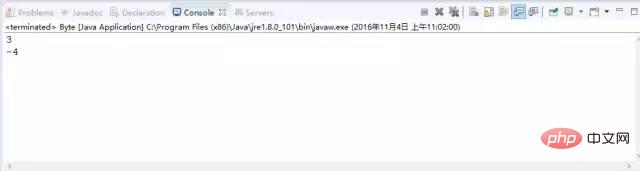
 Die Vorteile der Verwendung von Bitoperationen zum Austausch von zwei Zahlen Die dritte temporäre Variable ist nicht erforderlich (die Einschränkung besteht darin, dass nur Ganzzahlvariablen ausgetauscht werden können)
Die Vorteile der Verwendung von Bitoperationen zum Austausch von zwei Zahlen Die dritte temporäre Variable ist nicht erforderlich (die Einschränkung besteht darin, dass nur Ganzzahlvariablen ausgetauscht werden können) 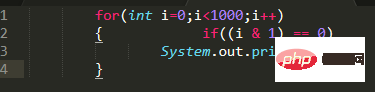 Analysieren Sie, wie der Austausch erfolgt: #🎜🎜 #Zuerst bedeutet a ^=b a=(a^b);
Analysieren Sie, wie der Austausch erfolgt: #🎜🎜 #Zuerst bedeutet a ^=b a=(a^b); b ist a= (a
b ist a= (a
 a = 3, b = 6
a = 3, b = 6