So verwenden Sie ein Dendrogramm, um visuelles Clustering in Python zu implementieren

Dendogramm

Ein Dendrogramm ist ein Diagramm, das hierarchische Beziehungen zwischen Objekten, Gruppen oder Variablen zeigt. Ein Dendrogramm besteht aus Zweigen, die an Knoten oder Clustern verbunden sind und Gruppen von Beobachtungen mit ähnlichen Merkmalen darstellen. Die Höhe eines Astes oder der Abstand zwischen den Knoten gibt an, wie unterschiedlich oder ähnlich die Gruppen sind. Das heißt, je länger die Zweige oder je größer der Abstand zwischen den Knoten, desto weniger ähnlich sind die Gruppen. Je kürzer die Zweige oder je geringer der Abstand zwischen den Knoten, desto ähnlicher sind die Gruppen.

Dendogramme eignen sich zur Visualisierung komplexer Datenstrukturen und zur Identifizierung von Untergruppen oder Datenclustern mit ähnlichen Merkmalen. Sie werden häufig in der Biologie, Genetik, Ökologie, Sozialwissenschaften und anderen Bereichen verwendet, in denen Daten basierend auf Ähnlichkeit oder Korrelation gruppiert werden können.

Hintergrundwissen:

Das Wort „Dendrogramm“ kommt von den griechischen Wörtern „dendron“ (Baum) und „gramma“ (Zeichnung). Im Jahr 1901 verwendete der britische Mathematiker und Statistiker Karl Pearson ein Baumdiagramm, um die Verwandtschaft zwischen verschiedenen Pflanzenarten darzustellen [1]. Er nannte dieses Diagramm ein „Clusterdiagramm“. Dies kann als die erste Verwendung von Dendrogrammen angesehen werden.

Datenaufbereitung

Wir werden die realen Aktienkurse mehrerer Unternehmen für die Clusterbildung nutzen. Für einen einfachen Zugriff werden die Daten mithilfe der kostenlosen API von Alpha Vantage erfasst. Alpha Vantage bietet sowohl eine kostenlose API als auch eine Premium-API. Für den Zugriff über die API ist ein Schlüssel erforderlich. Weitere Informationen finden Sie auf seiner Website.

import pandasaspd
import requests
 
 companies={'Apple':'AAPL','Amazon':'AMZN','Facebook':'META','Tesla':'TSLA','Alphabet (Google)':'GOOGL','Shell':'SHEL','Suncor Energy':'SU',
            'Exxon Mobil Corp':'XOM','Lululemon':'LULU','Walmart':'WMT','Carters':'CRI','Childrens Place':'PLCE','TJX Companies':'TJX',
            'Victorias Secret':'VSCO','MACYs':'M','Wayfair':'W','Dollar Tree':'DLTR','CVS Caremark':'CVS','Walgreen':'WBA','Curaleaf':'CURLF'}

20 ausgewählte Unternehmen aus den Branchen Technologie, Einzelhandel, Öl und Gas und anderen Branchen.

import time
 
 all_data={}
 forkey,valueincompanies.items():  
 # Replace YOUR_API_KEY with your Alpha Vantage API key
   url=f&#39;https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol={value}&apikey=<YOUR_API_KEY>&outputsize=full&#39;
   response=requests.get(url)
   data=response.json()
   time.sleep(15)
   if&#39;Time Series (Daily)&#39;indataanddata[&#39;Time Series (Daily)&#39;]:
     df=pd.DataFrame.from_dict(data[&#39;Time Series (Daily)&#39;], orient=&#39;index&#39;)
     print(f&#39;Received data for {key}&#39;)
   else:
     print("Time series data is empty or not available.")
   df.rename(columns= {&#39;1. open&#39;:key}, inplace=True)
   all_data[key]=df[key]

Der obige Code legt eine 15-sekündige Pause zwischen API-Aufrufen fest, um sicherzustellen, dass er nicht zu häufig blockiert wird.

# find common dates among all data frames
 common_dates=None
 fordf_key, dfinall_data.items():
     ifcommon_datesisNone:
         common_dates=set(df.index)
     else:
         common_dates=common_dates.intersection(df.index)
 
 common_dates=sorted(list(common_dates))
 
 # create new data frame with common dates as index
 df_combined=pd.DataFrame(index=common_dates)
 
 # reindex each data frame with common dates and concatenate horizontally
 fordf_key, dfinall_data.items():
     df_combined=pd.concat([df_combined, df.reindex(common_dates)], axis=1)

Integrieren Sie die oben genannten Daten in den von uns benötigten DF, der direkt unten verwendet werden kann

Hierarchisches Clustering

Hierarchisches Clustering ist ein Clustering-Algorithmus, der für maschinelles Lernen und Datenanalyse verwendet wird. Es verwendet eine Hierarchie verschachtelter Cluster, um ähnliche Objekte basierend auf ihrer Ähnlichkeit in Clustern zu gruppieren. Der Algorithmus kann entweder agglomerativ sein, also mit einzelnen Objekten beginnen und diese zu Clustern zusammenführen, oder divisiv, also mit einem großen Cluster beginnen und ihn rekursiv in kleinere Cluster aufteilen.

Es ist zu beachten, dass nicht alle Clustering-Methoden hierarchische Clustering-Methoden sind und Dendrogramme nur für einige wenige Clustering-Algorithmen verwendet werden können.

Clustering-Algorithmus Wir werden hierarchisches Clustering verwenden, das im Scipy-Modul bereitgestellt wird. 1. Top-Down-Clustering Anzahl der Farben. Die optimale Anzahl an Clustern ist eins weniger als die Anzahl an Farben. Gemäß dem Dendrogramm oben beträgt die optimale Anzahl von Clustern also zwei.

Eine weitere Möglichkeit, die optimale Anzahl von Clustern zu ermitteln, besteht darin, Punkte zu identifizieren, an denen sich der Abstand zwischen Clustern plötzlich ändert. Dies wird als „Kniepunkt“ oder „Ellenbogenpunkt“ bezeichnet und kann verwendet werden, um die Anzahl der Cluster zu bestimmen, die die Variation in den Daten am besten erfasst. In der obigen Abbildung können wir sehen, dass die maximale Abstandsänderung zwischen unterschiedlicher Anzahl von Clustern zwischen 1 und 2 Clustern auftritt. Auch hier beträgt die optimale Anzahl von Clustern zwei.

Erhalten Sie eine beliebige Anzahl von Clustern aus einem Dendrogramm.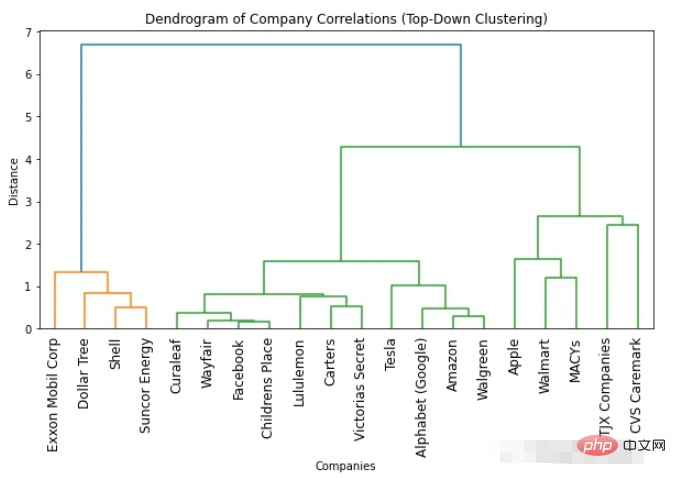

Ein Vorteil der Verwendung eines Dendrogramms besteht darin, dass Objekte durch Betrachten des Dendrogramms in eine beliebige Anzahl von Clustern gruppiert werden können. Wenn Sie beispielsweise zwei Cluster finden müssen, können Sie sich die obere vertikale Linie im Dendrogramm ansehen und sich für die Cluster entscheiden. Wenn in diesem Beispiel beispielsweise zwei Cluster erforderlich sind, gibt es vier Unternehmen im ersten Cluster und 16 Unternehmen im zweiten Cluster. Wenn wir drei Cluster benötigen, können wir den zweiten Cluster weiter in 11 und 5 Unternehmen aufteilen. Wenn Sie mehr benötigen, können Sie diesem Beispiel folgen.

2. Bottom-up-Clustering

import numpyasnp
import scipy.cluster.hierarchyassch
import matplotlib.pyplotasplt
 
 # Convert correlation matrix to distance matrix
 dist_mat=1-df_combined.corr()
 
 # Perform top-down clustering
 clustering=sch.linkage(dist_mat, method='complete')
 cuts=sch.cut_tree(clustering, n_clusters=[3, 4])
 
 # Plot dendrogram
 plt.figure(figsize=(10, 5))
 sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90)
 plt.title('Dendrogram of Company Correlations (Top-Down Clustering)')
 plt.xlabel('Companies')
 plt.ylabel('Distance')
 plt.show()

Das Dendrogramm, das wir für Bottom-up-Clustering erhalten, ähnelt dem Top-down-Clustering. Die optimale Clusteranzahl beträgt immer noch zwei (basierend auf der Anzahl der Farben und der „Wendepunkt“-Methode). Wenn wir jedoch mehr Cluster benötigen, werden einige subtile Unterschiede zu beobachten sein. Dies ist normal, da die verwendeten Methoden unterschiedlich sind, was zu geringfügigen Unterschieden in den Ergebnissen führt.

Das obige ist der detaillierte Inhalt vonSo verwenden Sie ein Dendrogramm, um visuelles Clustering in Python zu implementieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!