Analyse von Java-Beispielen für die Klassen BigInteger und BigDecimal mit großer Anzahl

BigInteger-Klasse

In Java gibt es viele Klassen, die verarbeitet werden müssen, z. B. die Integer-Klasse, aber auch die Integer-Klasse hat eine Obergrenze. Sein Maximalwert beträgt 2^31-1.

Wenn wir zu diesem Zeitpunkt eine größere Zahl darstellen möchten, kann diese nicht durch Integer dargestellt werden, daher stellt Java die Klasse BigInteger bereit.

Die von der BigInteger-Klasse unterstützten Zahlen können als unendlich bezeichnet werden, und sie unterstützt Ganzzahlen mit beliebiger Genauigkeit, was bedeutet, dass sie jeden Wert ohne Verlust genau darstellen kann.

Ich möchte hier auch betonen, dass Sie + - * /

nicht verwenden können, wenn Sie Operationen ausführen, da es sich bei dem eingehenden Nummerntyp um einen Zeichentyp handelt Verwenden Sie sie. Methoden:

add(), subtrahieren(), multiplizieren(), dividieren()

Es gibt auch einige gängige Methoden : #🎜 🎜#

equals-Methode. Vergleichen Sie

Codedemonstration:

import java.math.BigInteger;
public class Demo01 {
    public static void main(String[] args) {
        BigInteger bigInteger1 = new BigInteger("2222222222222222222222222222222");
        BigInteger bigInteger2 = new BigInteger("1111111111111111111111111111111");
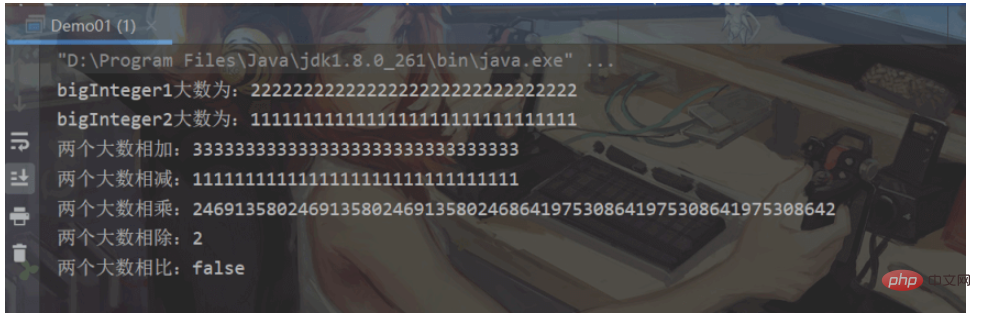
        System.out.println("bigInteger1大数为：" + bigInteger1);
        System.out.println("bigInteger2大数为：" + bigInteger2);
        System.out.println("两个大数相加：" + bigInteger1.add(bigInteger2));//加
        System.out.println("两个大数相减：" + bigInteger1.subtract(bigInteger2));//减
        System.out.println("两个大数相乘：" + bigInteger1.multiply(bigInteger2));//乘
        System.out.println("两个大数相除：" + bigInteger1.divide(bigInteger2));//除
        System.out.println("两个大数相比：" + bigInteger1.equals(bigInteger2));//equals进行比较
    }
}

Wenn bei der Division Dezimalstellen vorhanden sind, ist dies der Ort die Nachkommastellen werden abgeschnitten.

Natürlich gibt es nicht nur Integer-Typen, sondern auch Gleitkommatypen.

BigDecimal-Klasse

Natürlich kann die Genauigkeit des Gleitkommatyps auch so groß wie möglich sein.

import java.math.BigDecimal;
public class Demo02 {
    public static void main(String[] args) {
        BigDecimal bigDecimal1 = new BigDecimal("12232423432432.53241234324");
        BigDecimal bigDecimal2 = new BigDecimal("2.0");
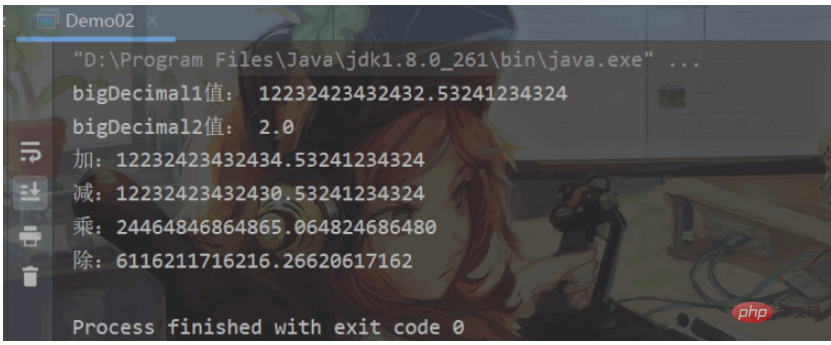
        System.out.println("bigDecimal1值： " + bigDecimal1);
        System.out.println("bigDecimal2值： " + bigDecimal2);
        System.out.println("加：" + bigDecimal1.add(bigDecimal2));
        System.out.println("减：" + bigDecimal1.subtract(bigDecimal2));
        System.out.println("乘：" + bigDecimal1.multiply(bigDecimal2));
        System.out.println("除：" + bigDecimal1.divide(bigDecimal2));
    }
}

In der BigDecimal-Methode kann es auch das Genauigkeitsproblem in der Java-Sprache besser lösen (z. B. das Ergebnis von 0,1x3 == 0,3). ist ein falsches Problem)

Das Problem der unvollständigen Division in der BigDecimal-Klasse

Aber es gibt auch einen Punkt, der gelöst werden muss Achten Sie darauf, wenn Sie BigDecimal verwenden. (Wenn es auf etwas stößt, das nicht geteilt werden kann, wird ein Fehler gemeldet.) , machen Sie einfach einen Abschnitt dafür. Nur die Anzahl der Ziffern.

Schauen wir uns zunächst eine Methode an:

public BigDecimal divisor(BigDecimal divisor, intscale, introundingMode)

#🎜 🎜 #Divisor - Divisor.

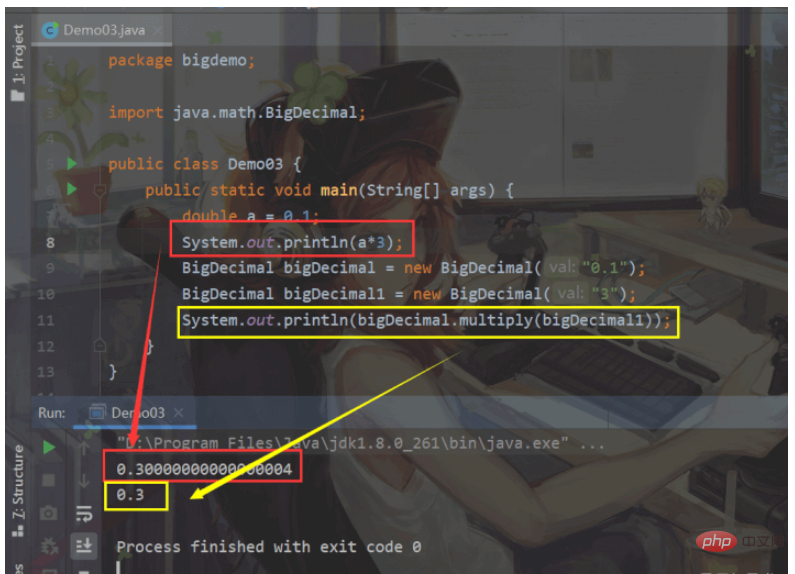
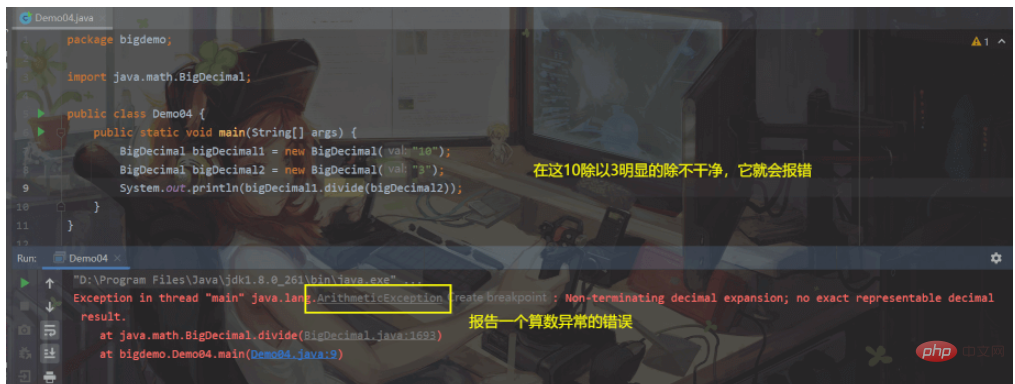
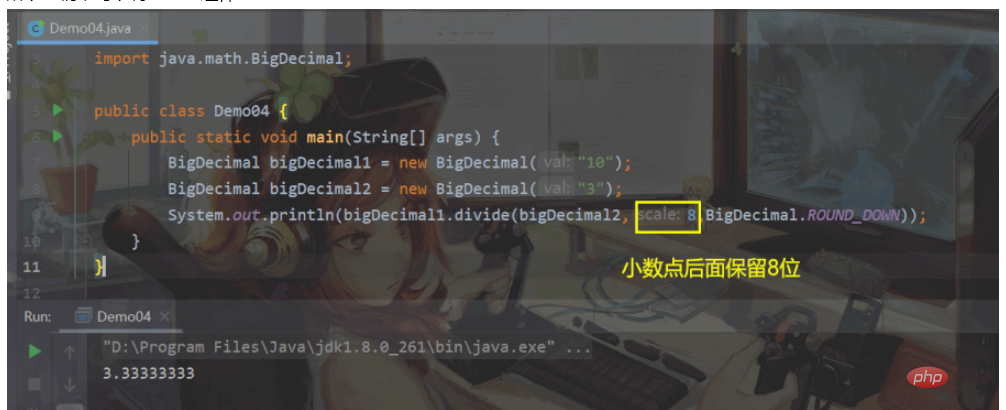
scale – Wie viele Dezimalstellen beibehalten werden sollen

roundingMode – Wählen Sie den Rundungsmodus

Damit wir es so schreiben können:

Auswahl des Rundungsmodus:

Modus

Bedeutung

ROUND_CEILINGBringe die Zahl auf positiv unendlich#🎜 🎜 #ROUND_DOWNROUND_FLOORROUND_HALF_DOWNBei Begegnung abrunden.5ROUND_HA LF_UP# 🎜 🎜#Runden Sie auf, wenn Sie auf .5 stoßen.Runden Sie auf, wenn Sie auf 5 stoßen, und schauen Sie sich die vorherige Zahl an, die größer als 5 ist oben, kleiner als 5 ist unten, gleich 5 und dann schauen Sie nach vorne.

Bringe die Zahl in Richtung 0
Bringe die Zahl in Richtung negative Unendlichkeit #🎜 🎜#
	ROUND_HALF_EVEN

Das obige ist der detaillierte Inhalt vonAnalyse von Java-Beispielen für die Klassen BigInteger und BigDecimal mit großer Anzahl. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!