Beispielanalyse von Union-Find in Java

1. Übersicht

Union-Find: eine baumartige Datenstruktur, die zur Lösung einiger Zusammenführungs- und Abfrageprobleme disjunkter Mengen verwendet wird. Beispiel: Es gibt n Dörfer. Fragen Sie ab, ob es eine Verbindungsstraße zwischen den beiden Dörfern gibt, die die beiden Dörfer verbindet zwei Die Elementmengen werden zu einer Menge zusammengeführt

2. Implementierung

Es gibt zwei gängige Implementierungsideen

Schnellsuche

Zeitliche Komplexität von Find: O(1)

Zeitliche Komplexität von Union: O (n)
Quick Union
Zeitkomplexität von Find: O(logn) kann auf O(a (n))a(n)
Zeitkomplexität von Union: O (logn) kann mithilfe von auf O(a(n))a(n)
optimiert werden. Das Array implementiert eine Baumstruktur, der Array-Index ist das Element und der im Array gespeicherte Wert ist der Wert des übergeordneten Knotens

Erstellen Sie die abstrakte Klasse Union Find

public abstract class UnionFind {
 
	 int[] parents;
	/**
	 * 初始化并查集
	 * @param capacity
	 */
	public UnionFind(int capacity){
		
		if(capacity < 0) {
			throw new IllegalArgumentException("capacity must be >=0");
		}
        //初始时每一个元素父节点（根结点）是自己
		parents = new int[capacity];
		for(int i = 0; i < parents.length;i++) {
			parents[i] = i;
		}
	}
	
   /**
     *  检查v1 v2 是否属于同一个集合
     */
	public boolean isSame(int v1,int v2) {
		return find(v1) == find(v2);
	}
 
    /**
     *  查找v所属的集合 （根节点）
     */
	public  abstract int find(int v);
 
	/**
     *  合并v1 v2 所属的集合
     */
	public abstract void union(int v1, int v2);
	
		
	// 范围检查
	public   void rangeCheck(int v)  {
		if(v<0 || v > parents.length)
			throw new IllegalArgumentException("v is out of capacity");
	}
}

2.1 Quick Find-Implementierung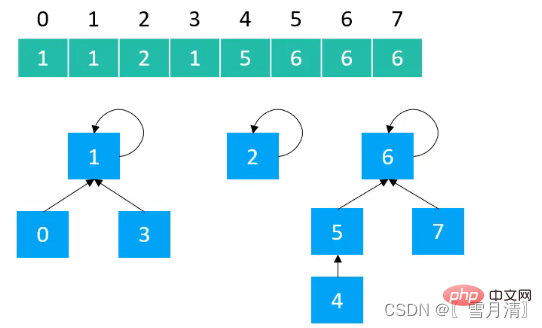

Union-Suche mit Quick Find implementiert, Baum Die maximale Höhe von Wenn der Baum unausgeglichen ist

Es gibt zwei Optimierungen Ideen: Rangoptimierung und Größenoptimierung
3.1 Größenbasierte Optimierung

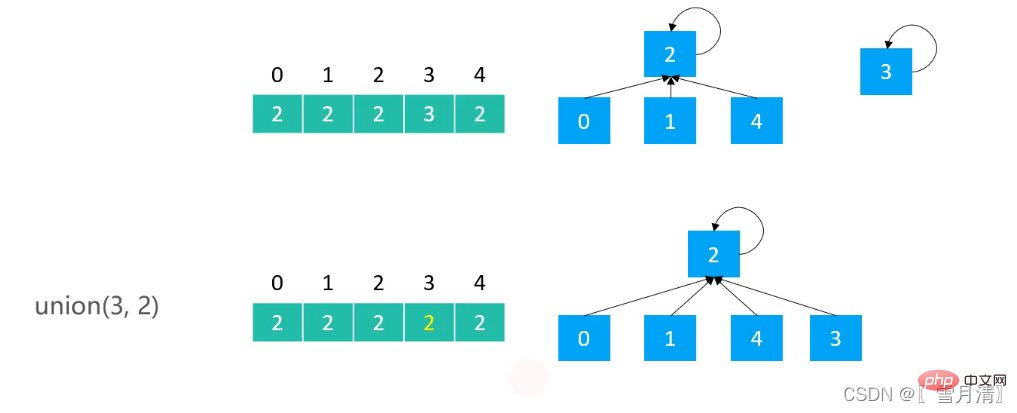Kernidee: Ein Baum mit wenigen Elementen wird auf einen Baum mit vielen Elementen gepfropft

public class UnionFind_QF extends UnionFind {
	public UnionFind_QF(int capacity) {
		super(capacity);
		
	}
 
  // 查
@Override
	public  int  find(int v) {
		rangeCheck(v);
		return parents[v];
	}
 
 // 并 将v1所在集合并到v2所在集合上
@Override
public void union(int v1, int v2) {
    // 查找v1 v2 的父（根）节点
	int p1= find(v1);
	int p2 = find(v2);
	if(p1 == p2) return;
  
    //将所有以v1的根节点为根节点的元素全部并到v2所在集合上 即父节点改为v2的父节点
	for(int i = 0; i< parents.length; i++) {
		if(parents[i] == p1) {
			parents[i] = p2;
		}
	}
	
  }
}

Größenbasierte Optimierung Es kann auch dazu führen, dass der Baum unausgeglichen ist

3.2 Rangbasierte Optimierung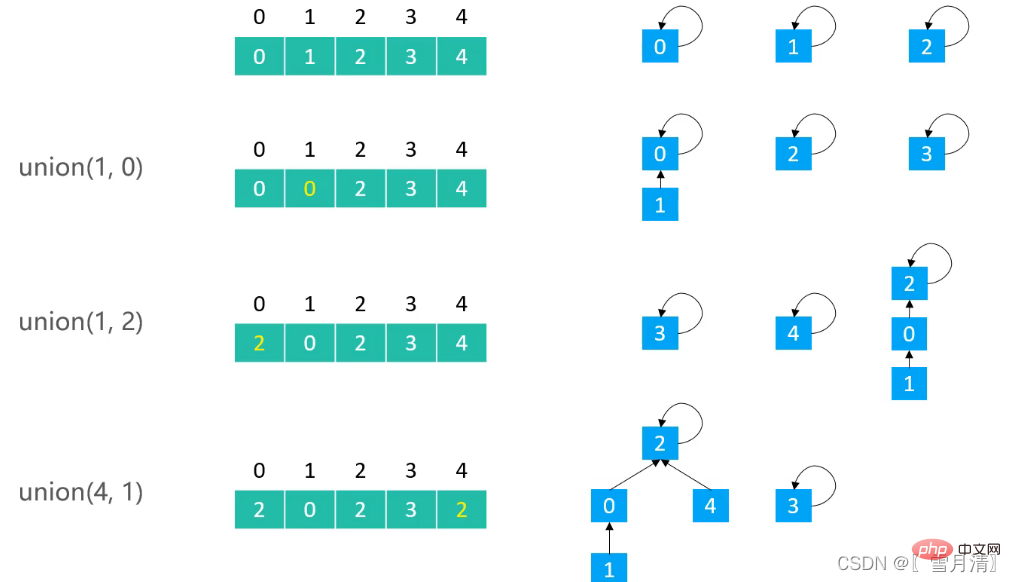

Kernidee: Einen kurzen Baum auf einen hohen Baum pfropfen

public class UnionFind_QU extends UnionFind {
 
	public UnionFind_QU(int capacity) {
		super(capacity);
		
	}
 
	//查某一个元素的根节点
	@Override
	public int find(int v) {
   //检查下标是否越界
		rangeCheck(v);
   
  // 一直循环查找节点的根节点
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
//V1 并到 v2 中
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
      //将v1 根节点 的 父节点 修改为 v2的根结点 完成合并
		parents[p1] = p2;
	}
}

Basierend auf der Rangoptimierung wird die Höhe des Baums mit zunehmender Anzahl von Gewerkschaften immer höher und höher. Dadurch wird der Suchvorgang langsamer down
Es gibt drei Ideen, die weiter optimiert werden müssen: Pfadkomprimierung, Pfadaufteilung und Pfadhalbierung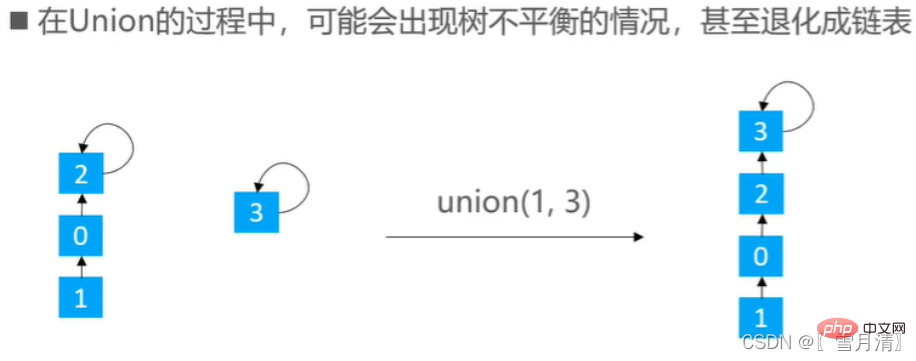

3.2.1 Pfadkomprimierung (Pfadkomprimierung)

Alle Knoten auf dem Pfad zeigen beim Suchen auf den Wurzelknoten. Dadurch wird die reduziert Höhe des Baums

public class UniondFind_QU_S extends UnionFind{
 
   // 创建sizes 数组记录 以元素（下标）为根结点的元素（节点）个数
	private int[] sizes;
 
	public UniondFind_QU_S(int capacity) {
		super(capacity);
 
		sizes = new int[capacity];
 
   //初始都为 1
		for(int i = 0;i < sizes.length;i++) {
			sizes[i] = 1;
			}
		
	}
 
	@Override
	public int find(int v) {
 
		rangeCheck(v);
 
		while (v != parents[v]) {
			v = parents[v];
		}
		return v;
	}
 
	@Override
	public void union(int v1, int v2) {
	
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
 
		//如果以p1为根结点的元素个数 小于 以p2为根结点的元素个数 p1并到p2上，并且更新p2为根结点的元素个数
	if(sizes[p1] < sizes[p2]) {
		    parents[p1] = p2;
		    sizes[p2] += sizes[p1];
		
 // 反之 则p2 并到 p1 上，更新p1为根结点的元素个数
	}else {
			parents[p2] = p1;
			sizes[p1] += sizes[p2];
		}
	}
}

Obwohl es die Höhe des Baums reduzieren kann, sind die Implementierungskosten etwas höher
3.2.2 Pfadaufteilung
Lassen Sie jeden Knoten auf dem Pfad auf seinen übergeordneten Knoten zeigen

public class UnionFind_QU_R extends UnionFind_QU {
   // 创建rank数组  ranks[i] 代表以i为根节点的树的高度
 private int[] ranks;
 
	public UnionFind_QU_R(int capacity) {
		super(capacity);
 
		ranks = new int[capacity];
 
		for(int i = 0;i < ranks.length;i++) {
			ranks[i] = 1;
		}
 
	}
    
	public void union(int v1, int v2) {
 
		int p1 = find(v1);
		int p2 = find(v2);
		if(p1 == p2) return;
    
    // p1 并到 p2 上 p2为根 树的高度不变
		if(ranks[p1] < ranks[p2]) {
			parents[p1] = p2;
			
  // p2 并到 p1 上 p1为根 树的高度不变
		} else if(ranks[p1] > ranks[p2]) {
			parents[p2] = p1;
 
		}else {
    // 高度相同 p1 并到 p2上，p2为根 树的高度+1
			parents[p1] = p2;
			ranks[p2] += 1;
		}
	}
}

3.2.3 Pfadhalbierung

Lassen Sie jeden zweiten Knoten auf dem Pfad auf seinen übergeordneten Knoten zeigen

/**
 *  Quick Union -基于rank的优化  -路径压缩
 *
 */
public class UnionFind_QU_R_PC extends UnionFind_QU_R {
 
	public UnionFind_QU_R_PC(int capacity) {
		super(capacity);
		
	}
 
	@Override
	public int find(int v) {
		rangeCheck(v);
 
		if(parents[v] != v) {
 
        //递归 使得从当前v 到根节点 之间的 所有节点的 父节点都改为根节点
			parents[v] = find(parents[v]);
		}
		return parents[v];
	}
}

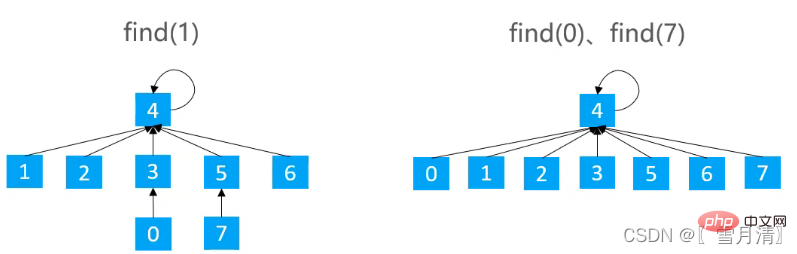Verwenden Sie Quick Union + rangbasierte Optimierung + Pfadaufteilung oder Pfadhalbierung

Es kann garantiert werden, dass sich die Werte amortisieren Die zeitliche Komplexität jeder Operation beträgt O(a(n)), a(n)

Das obige ist der detaillierte Inhalt vonBeispielanalyse von Union-Find in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!