Heim >Java >javaLernprogramm >Ausführliche Erläuterung von Beispielen zum Hinzufügen, Einfügen, Löschen und Erstellen binärer Java-Suchbäume
Ausführliche Erläuterung von Beispielen zum Hinzufügen, Einfügen, Löschen und Erstellen binärer Java-Suchbäume
- PHPznach vorne
- 2023-04-25 16:40:081623Durchsuche
①Konzept
Der binäre Suchbaum wird auch als binärer Sortierbaum bezeichnet. Er ist entweder ein leerer Baum** oder ein binärer Baum mit den folgenden Eigenschaften:
Wenn sein linker Teilbaum nicht leer ist, dann die Werte aller Knoten im linken Teilbaum sind kleiner als der Wert des Wurzelknotens
Wenn sein rechter Teilbaum nicht leer ist, dann sind die Werte aller Knoten im rechten Teilbaum größer als der Wert des Wurzelknotens
Seine linken und rechten Teilbäume sind jeweils auch der binäre Suchbaum Operation - Einfügen



public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}④Operation-Delete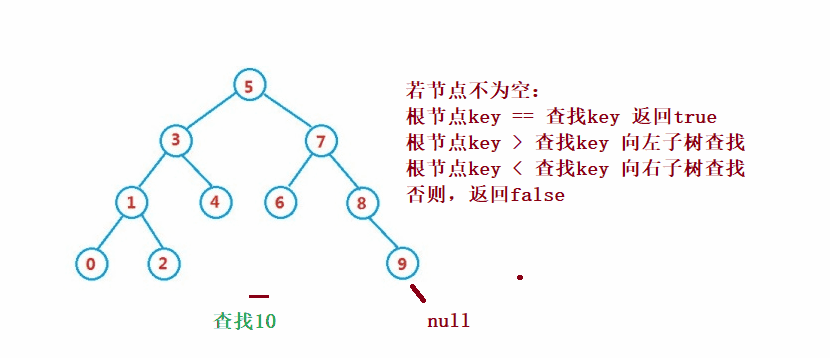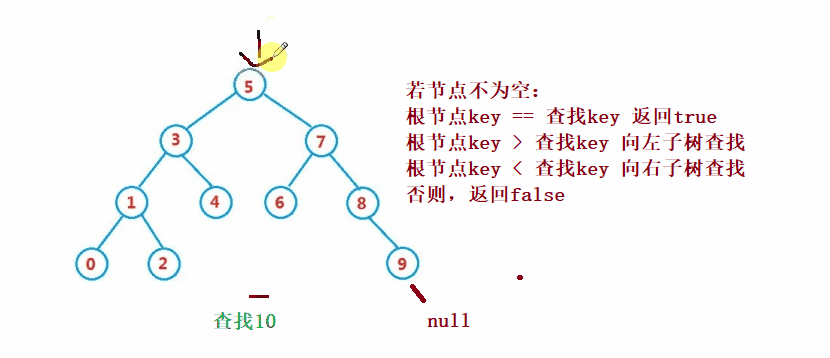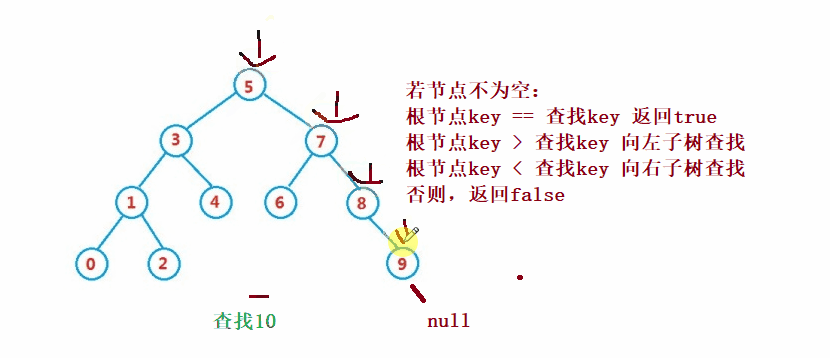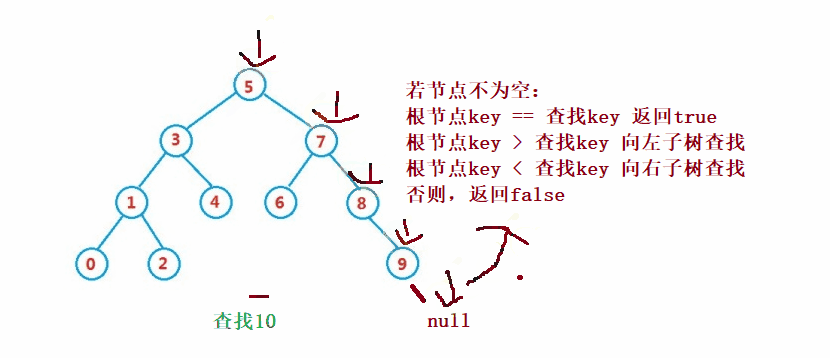 Der Löschvorgang ist komplizierter, aber sein Prinzip ist relativ einfach zu verstehen
Der Löschvorgang ist komplizierter, aber sein Prinzip ist relativ einfach zu verstehen
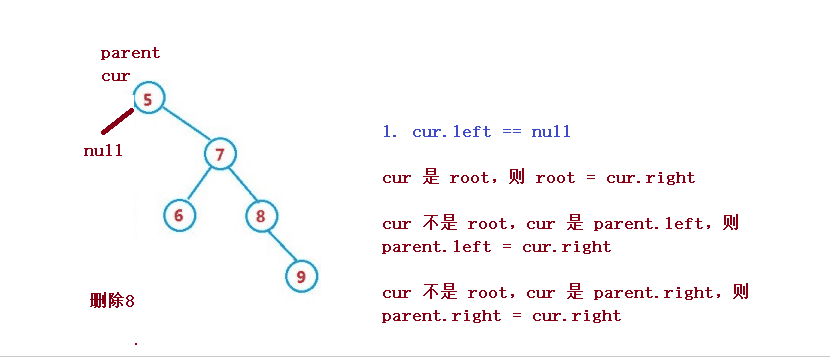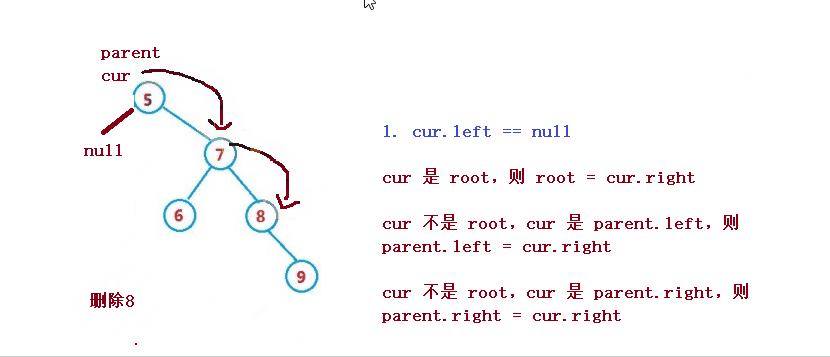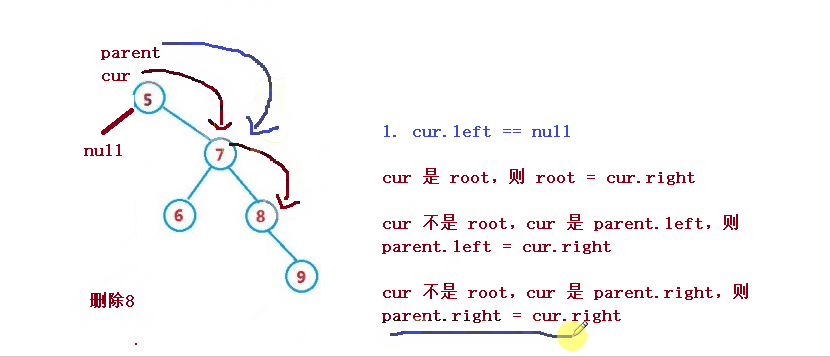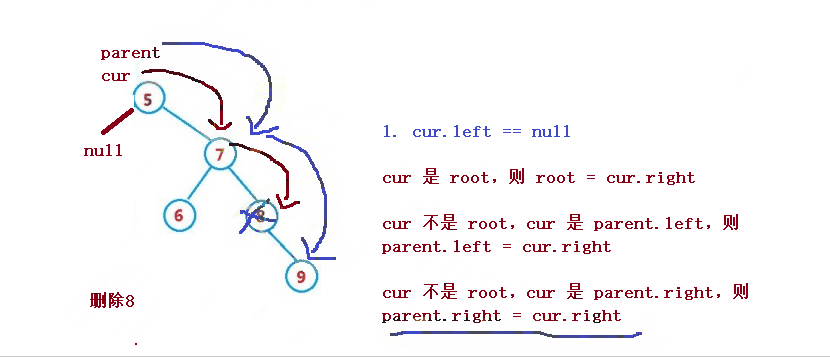
Angenommen, der zu löschende Knoten ist cur, und der übergeordnete Knoten des zu löschenden Knotens ist parent
1. cur.left == null
 2 , dann ist parent.left = cur.right
2 , dann ist parent.left = cur.right
3. cur ist nicht root, cur ist parent.right, dann ist parent.right = cur.right
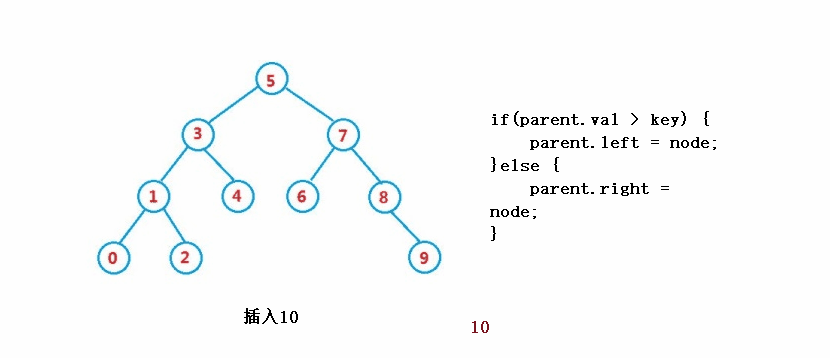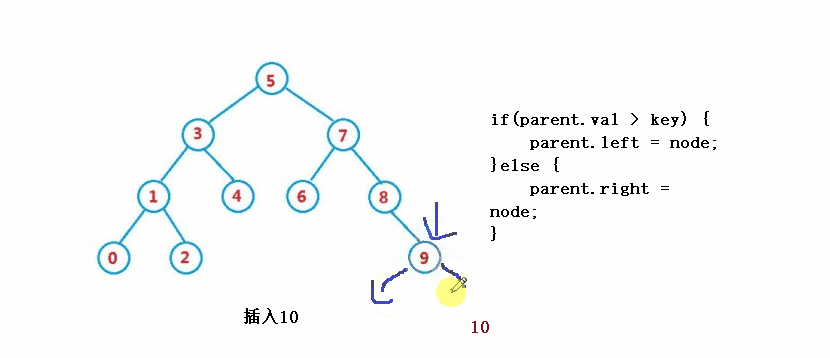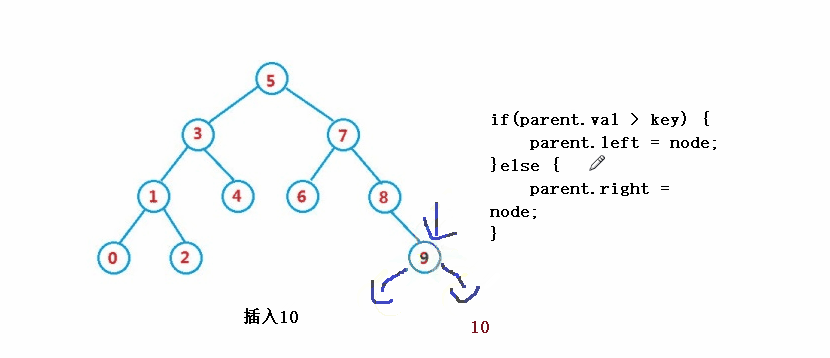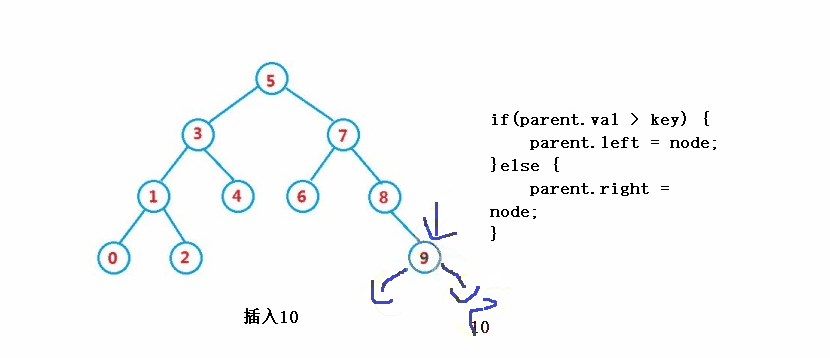
2. right == null
1. cur ist root, dann ist root = cur .left
2. cur ist nicht root, cur ist parent.left, dann ist parent.left = cur.left
3. cur ist parent.right, dann parent.right = cur.left
 3. richtig != null
3. richtig != null
Sie müssen zum Löschen die Substitutionsmethode verwenden, d Behandeln Sie das Löschproblem des Knotens
 Wenn für einen binären Suchbaum mit n Knoten die Wahrscheinlichkeit der Suche nach jedem Element gleich ist, ist die durchschnittliche Suchlänge des binären Suchbaums eine Funktion der Tiefe des Knotens im binären Suchbaum, d. h. Je tiefer der Knoten, desto mehr Vergleiche gibt es.
Wenn für einen binären Suchbaum mit n Knoten die Wahrscheinlichkeit der Suche nach jedem Element gleich ist, ist die durchschnittliche Suchlänge des binären Suchbaums eine Funktion der Tiefe des Knotens im binären Suchbaum, d. h. Je tiefer der Knoten, desto mehr Vergleiche gibt es.
Wenn jedoch für denselben Schlüsselcodesatz die Reihenfolge der Einfügung jedes Schlüsselcodes unterschiedlich ist, können binäre Suchbäume mit unterschiedlichen Strukturen erhalten werden:
Im optimalen Fall ist der binäre Suchbaum ein vollständiger binärer Baum und seine durchschnittliche Anzahl an Vergleichen beträgt:
Im schlimmsten Fall degeneriert der binäre Suchbaum zu einem einzelnen Zweigbaum und seine durchschnittliche Anzahl an Vergleichen beträgt:⑥完整代码
public class TextDemo {
public static class Node {
public int val;
public Node left;
public Node right;
public Node (int val) {
this.val = val;
}
}
public Node root;
/**
* 查找
* @param key
*/
public Node search(int key) {
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val < key) {
cur = cur.right;
}else {
cur = cur.left;
}
}
return null;
}
/**
*
* @param key
* @return
*/
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
root = node;
return true;
}
Node cur = root;
Node parent = null;
while(cur != null) {
if(cur.val == key) {
return false;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
//parent
if(parent.val > key) {
parent.left = node;
}else {
parent.right = node;
}
return true;
}
public void remove(Node parent,Node cur) {
if(cur.left == null) {
if(cur == root) {
root = cur.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = cur.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}
}
}
public void removeKey(int key) {
if(root == null) {
return;
}
Node cur = root;
Node parent = null;
while (cur != null) {
if(cur.val == key) {
remove(parent,cur);
return;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else {
parent = cur;
cur = cur.left;
}
}
}
}Das obige ist der detaillierte Inhalt vonAusführliche Erläuterung von Beispielen zum Hinzufügen, Einfügen, Löschen und Erstellen binärer Java-Suchbäume. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Wie lade ich Dateien mit zusätzlichen Parametern mithilfe von java.net.URLConnection und Multipart/Form-Data-Codierung hoch?
- Wie aktualisiere ich ein JLabel kontinuierlich mit Swing Timer und SwingWorker?
- Wie validiere ich die JTable-Zelleneingabe auf nicht positive Ganzzahlwerte?
- Was sind die Hauptunterschiede zwischen Schnittstellen und abstrakten Klassen in Java?
- Wie greife ich auf dynamische Schlüssel in verschachtelten JSON-Ergebnissen zu?

