Java-Rekursion: Konzepte und Verwendung

1. Das Konzept der Rekursion

1.

Rekursion ist: der Prozess, bei dem eine Methode selbst aufgerufen wird.

Es gibt zwei Voraussetzungen für die Verwendung der Rekursion:

1 Es gibt eine Annäherungs- und Beendigungsbedingung.

2. Rufen Sie sich selbst an.

Wie implementiert man eine Rekursion?

Der wichtigste Weg ist: Um die Rekursion zu implementieren, müssen Sie eine Rekursionsformel ableiten.

Die Art und Weise, über Rekursion nachzudenken: Denken Sie seitlich und denken Sie gemäß der rekursiven Formel.

Codeausführung: vertikale Ausführung.

2. Erklärung der Rekursion

Schauen Sie sich zunächst den folgenden Code an:

public class TestDemo {
    public static void func(){
        
        func();   //自己调用自己本身
    }
 
 
    public static void main(String[] args) {
        func();
 
    }
}

Der obige Code ist eine einfache Rekursion.

Schauen wir uns noch einmal die laufenden Ergebnisse dieses Codes an.

Bilderklärung:

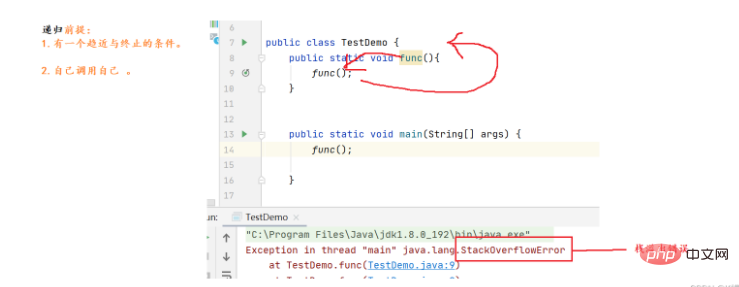
Für die Rekursion im Bild oben gibt es keine Bedingung, die dazu neigt, zu enden, sodass diese Funktion endlos rekursiv ist. Bei jeder Rekursion muss Speicher auf dem Stapel zugewiesen werden. Wenn Sie weiterhin Speicher auf dem Stapel zuweisen, läuft der Stapel möglicherweise über.

Veteranen, bitte denken Sie daran: Wenn bei der von Ihnen geschriebenen Rekursion ein Problem auftritt und die Grenze nicht korrekt gefunden wird, wird auf jeden Fall ein Fehler gemeldet. Wenn dieser Fehler gemeldet wird, muss es sich um Ihre Kündigung handeln Die Bedingung ist falsch oder das Versäumnis, eine Beendigungsbedingung zu schreiben, führt dazu, dass Sie zu tief in den rekursiven Prozess vordringen und schließlich der Stapel überläuft.

Wenn wir möchten, dass der obige Code korrekt ist, müssen wir ihm eine Beendigungsbedingung hinzufügen.

Der korrekte Code lautet wie folgt:

public class TestDemo {
    public static void func(int n){
        if(n == 1) return;
        func(n -1);
    }
 
 
    public static void main(String[] args) {
        func(3);
 
    }
}

Das Folgende vermittelt Ihnen anhand einfacher Beispiele ein tieferes Verständnis der Rekursion

2. Verwendung der Rekursion

Beispiel: Finden Sie die Fakultät von n rekursiv. Zeichnungsanalyse:

Implementierungscode:

public class TestDemo {
    public static int fac(int n){
        if(n == 1) {
            return 1;
        }
        int tmp = n * fac(n - 1);
        return tmp;
    }
    public static void main(String[] args) {
        System.out.println(fac(5));
 
    }
}

Erläuterung der Codezeichnung:

Beispiel: Ermitteln Sie die Summe von n

Zeichnungsanalyse: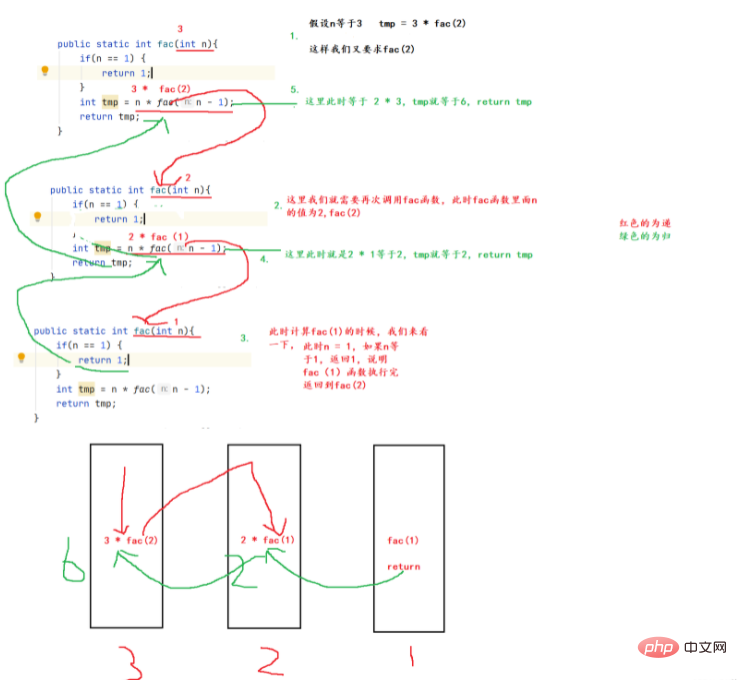

Implementierungscode:

第一种写法：
public class TestDemo {
    public static int sumAdd(int n){
        if(n == 1) {
            return 1;
        }
        int tmp = n + sumAdd(n - 1);
        return tmp;
    }
    public static void main(String[] args) {
        System.out.println(sumAdd(3));
 
    }
}
 
第二种写法：
public class TestDemo {
    public static int sumAdd(int n){
        if(n == 1) {
            return 1;
        }
       
        return n + sumAdd(n -1);
    }
    public static void main(String[] args) {
        System.out.println(sumAdd(3));
 
    }
}

Beispiel: Die rekursive Implementierung druckt jede Ziffer der Reihe nach

Zeichnung Analyse:

Implementierungscode:

public class TestDemo {
 
    public static void print(int n){
        if(n < 10){
            System.out.print(n+" ");
        }else{
            print(n/10);
            System.out.print(n%10+" ");
        }
    }
    public static void main(String[] args) {
        print(1234);
 
 
    }
}

Beispiel: Schreiben Sie eine rekursive Methode, geben Sie eine nicht negative Ganzzahl ein und geben Sie die Summe der Zahlen zurück, aus denen sie besteht. Beispiel: Wenn Sie 1729 eingeben, sollte 1+7+2+9 zurückgegeben werden.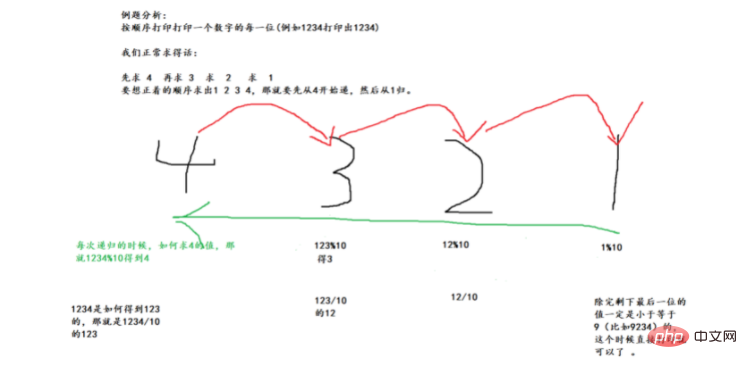

Implementierungscode:

public class TestDemo {
 
 
    public static int sumEveryone(int n){
        if(n < 10){
           return n;
        }else{
            return n%10 + sumEveryone(n/10);
        }
    }
 
    public static void main(String[] args) {
        System.out.println(sumEveryone(7910));
 
    }
 
}

Beispielfrage: Finden Sie die n-te Fibonacci-Zahl

Das obige ist der detaillierte Inhalt vonJava-Rekursion: Konzepte und Verwendung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!