|
Dies sind sehr grundlegende Kenntnisse, aber wenn Sie sie nicht zu lange verwenden, werden Sie sie unweigerlich vergessen. Sie können sie beim Codieren häufiger verwenden!
Sprechen ist günstig, zeigen Sie mir den Code.
Hinweis: Es ist wirklich schwierig, die Anwendung zu erkennen, wenn Sie diese allein besprechen. Wenn etwas nicht klar ist, können Sie sich die Zusammenfassungen anderer Leute ansehen.
Sehen wir uns die Anwendung von Bitoperationen mit einem Code an:
public final void writeInt(int v) throws IOException {
out.write((v >>> 24) & 0xFF);
out.write((v >>> 16) & 0xFF);
out.write((v >>> 8) & 0xFF);
out.write((v >>> 0) & 0xFF);
incCount(4);
}Dieser Code ist DataOutputStream 类中的一个方法,用于将一个 int 型的整数写入流中。这个方法的命名是很有意思的,它和 OutputStream 中的 public abstract void write(int b) throws IOException Diese Methode ist völlig anders. Die Parameter dieser Methode scheinen darauf hinzuweisen, dass sie eine Ganzzahl in den Stream schreiben kann, die Funktion der Methode wird jedoch nicht erraten, sondern hängt von der Beschreibung der Methode ab. Einführung in
public abstract void write(int b) throws IOException
API:
Schreibt das angegebene Byte in diesen Ausgabestream. Der allgemeine Vertrag für write besteht darin, dass ein Byte in den Ausgabestream geschrieben wird das Argument b Die 24 höherwertigen Bits von b werden ignoriert.
Es schreibt ein bestimmtes Byte in den Stream. Wir wissen, dass eine int-Variable 32 Bits und ein Byte 8 Bits belegt, also das letzte 8 Bits einer Ganzzahl vom Typ int kleiner als 256 (2^8) und eine Ganzzahl vom Typ Byte sind gleich.
Diese Methode besteht also darin, die niedrigsten 8 Bits einer int-Variablen zu schreiben und die restlichen 24 Bits zu ignorieren. Seien Sie bei dieser Methode besonders vorsichtig!
Das zu schreibende Byte sind die acht niederwertigen Bits des Arguments b. Die 24 höherwertigen Bits von b werden ignoriert.
Schreiben Sie also eine int-Variable vollständig im Fluss ist kein sehr einfaches Problem. Kehren wir zum obigen Code zurück: Er wird viermal hintereinander geschrieben, wobei jedes Mal ein Datenbyte geschrieben wird. Auf diese Weise wird eine Variable vom Typ int in 4 Bytes umgewandelt und in den Stream geschrieben.
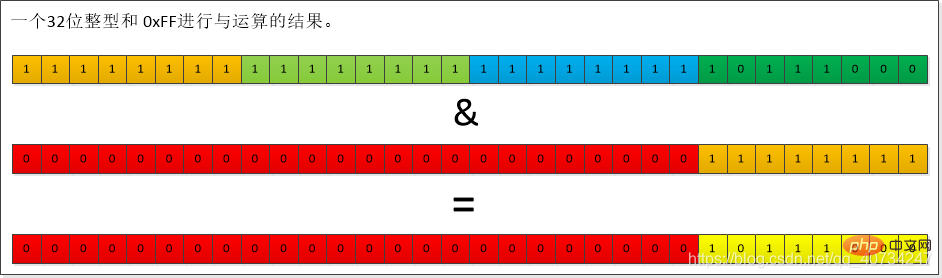
out.write((v >>> 24) & 0xFF); Diese Methode dient zum Schreiben der unteren 8-stelligen Zahl oben. Diese spezifische Implementierung wird von der entsprechenden Unterklasse bereitgestellt.
Schauen wir uns das Diagramm an: Eine einfache UND-Operation: Es ist ersichtlich, dass das Ergebnis der Operation die unteren 8 Bits beibehält. Dies ist das Ergebnis von (v>>>24) & 0xFF Betrieb.

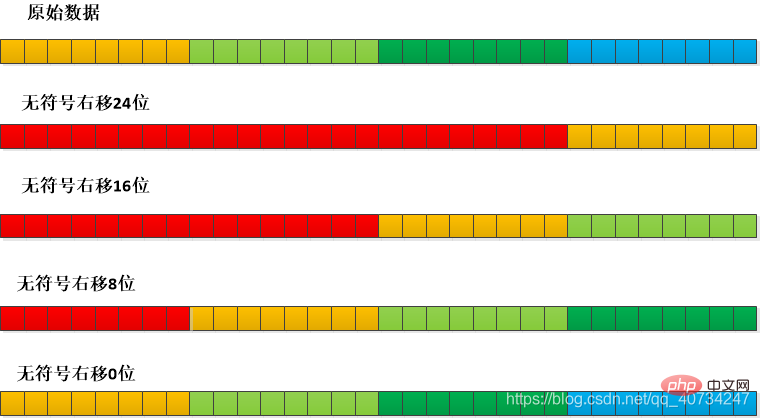
Wie erhält man also den hohen 8-Bit-Wert? Dies erfordert die Verwendung von Schiebeoperationen:

Durch die Schiebeoperation können Sie alle 8-Bit-Daten abrufen und dann die bitweise UND-Operation ausführen, um eine Ganzzahl vollständig in den Fluss zu schreiben.
Code-Demonstration
Code
package dragon;
/**
* 分析这一个方法,目前水平有限,先从最简单的做起!
* */
// public final void writeInt(int v) throws IOException {
// out.write((v >>> 24) & 0xFF);
// out.write((v >>> 16) & 0xFF);
// out.write((v >>> 8) & 0xFF);
// out.write((v >>> 0) & 0xFF);
// incCount(4);
// }
//上面这段代码是将一个32位整型,写入输出流。
//并且是将32位整型分为4个部分,每次写入8位。
//这是Java的特性。
public class DataOutputStreamAnalysis {
public static void main(String[] args) {
DataOutputStreamAnalysis analysis = new DataOutputStreamAnalysis();
analysis.analysis(65535);
}
public void analysis(int number) {
int number1, number2, number3, number4; //后面的数字表示是一个32位整型的第几个8位。
number1 = (number >>> 24) & 0xFF;
number2 = (number >>> 16) & 0xFF;
number3 = (number >>> 8) & 0xFF;
number4 = (number >>> 0) & 0xFF;
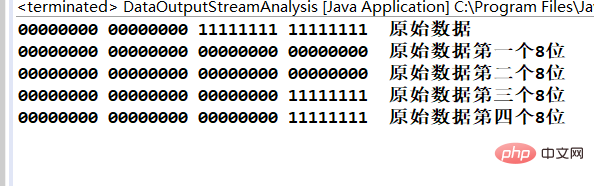
System.out.println(this.format(Integer.toBinaryString(number))+" 原始数据");
System.out.println(this.format(Integer.toBinaryString(number1))+" 原始数据第一个8位");
System.out.println(this.format(Integer.toBinaryString(number2))+" 原始数据第二个8位");
System.out.println(this.format(Integer.toBinaryString(number3))+" 原始数据第三个8位");
System.out.println(this.format(Integer.toBinaryString(number4))+" 原始数据第四个8位");
}
/**
* 输入一个二进制字符串,将其格式化,因为整型是
* 占32位的,但是转换成的二进制字符串,并没有32位*/
public String format(String bstr) {
int len = bstr.length();
StringBuilder sb = new StringBuilder(35);
for (int i = 0; i < 32-len; i++) {
sb.append("0");
}
sb.append(bstr);
sb.insert(8, " ");
sb.insert(17, " ");
sb.insert(26, " "); //前面插入一个字符后,所有字符的索引都变了!
return sb.toString();
}
}Ergebnis

Erläuterung: Der Fall negativer Zahlen wird hier nicht berücksichtigt, aber sie sind alle gleich, außer dass der Ausdruck negativer Zahlen etwas schwieriger ist. Solange Sie positive Zahlen verstehen, sind negative Zahlen kein Problem.
Anwendung von Bitoperationen
1. Bestimmen Sie, ob die Variable vom Typ int ist
if (x & 1 ==0)
System.out.println("x是偶数");
if (x & 1 == 1)
System.out.println("x是奇数");Erklärung: Dies ist immer noch leicht zu verstehen, da die letzte Verschiebung gerader Zahlen 0 sein muss. (Binäre Darstellung)
2. Nehmen Sie das k-te Bit der Variablen vom Typ int
Ausdruck: x >> k & 1 (Es wird empfohlen, Klammern hinzuzufügen, um es klarer zu machen.)
3 Setzen Sie die k-te Position der Variablen vom Typ int auf 1 Verschieben Sie 1 auf um k Bits links und führen Sie dann eine logische ODER-Verknüpfung mit der Variablen x durch. Dann wird das k-te Bit der Variablen x auf 1 gesetzt und die anderen Bits bleiben unverändert.
Ausdruck: x = x |. (1
4. Löschen Sie das k-te Bit der Variable vom Typ int auf 0 Verschieben Sie 1 um k Bits nach links, invertieren Sie die Ergebnisse, und die Ergebnisse summieren. Wenn eine logische Operation unter der Variablen ausgeführt wird, wird das k-te Bit der Variablen x auf 0 gelöscht und die anderen Bits bleiben unverändert.
Ausdrucksbits: x = x & ~(1
5. Berechnen Sie den Durchschnitt zweier Ganzzahlen
Ausdrucksbits: (x & y) + ((x ^ y) > Formel: x = x
Zum Beispiel: Erweitern Sie x um das 2-fache: x = x
Der Grund, warum bitweise Operationen empfohlen werden:
Bitweise Operationen sind schneller als arithmetische Operationen, da bitweise Operationen weniger Anweisungen erfordern und weniger Zeit für die Ausführung benötigen. Sie scheinen sehr schnell zu sein, aber die Vorteile bitweiser Operationen zeigen sich erst, wenn eine große Anzahl von Ausführungen durchgeführt wird. Schließlich werden die Computer von heute immer schneller.