Heim >Java >javaLernprogramm >Design und Analyse von Java-Algorithmen: Detaillierte Erläuterung von Beispielen für Divide-and-Conquer-Algorithmen
Design und Analyse von Java-Algorithmen: Detaillierte Erläuterung von Beispielen für Divide-and-Conquer-Algorithmen
- 王林nach vorne
- 2023-04-23 11:22:07822Durchsuche
1. Einführung
Bevor ich den Divide-and-Conquer-Algorithmus lerne, möchte ich Ihnen eine Frage stellen. Ich glaube, alle haben gerettet Geld, als sie jung waren. Wenn Eltern und Verwandte Geld geben, werden sie ab und zu Geld in ihre eigenen Schätze stecken. Es kann jedoch schwierig sein, mit einem Haufen Geld umzugehen, da die Daten im Vergleich zu Ihrem Gehirn etwas groß sind und es leicht ist, Fehler zu machen. Sie können sie in mehrere kleine Teile aufteilen und diese dann addieren, um die Gesamtsumme zu berechnen . Der Gesamtbetrag dieses Geldhaufens beträgt
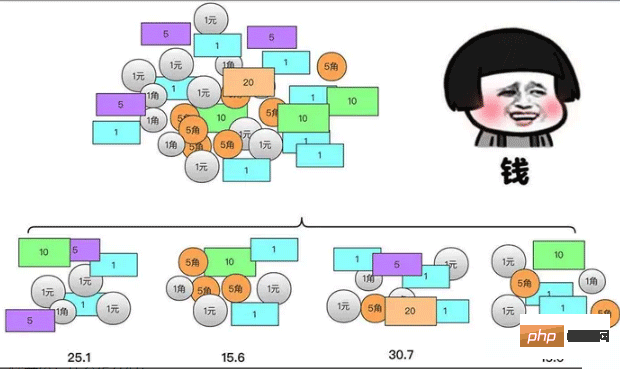
Natürlich, wenn Sie denken, dass der Betrag jedes Teils des Geldes immer noch zu groß ist, Sie kann es immer noch teilen und zusammenführen. Der Grund, warum wir das tun, liegt vor allem daran, dass:
-
Die Art und Weise, jeden kleinen Geldhaufen zu berechnen, ist die gleiche wie die größter Geldhaufen (der Unterschied liegt in der Größe)
# 🎜🎜# - Dann ist die Summe des großen Geldhaufens tatsächlich die Summe der Ergebnisse des kleinen Geldhaufens . Auf diese Weise herrscht tatsächlich eine Teile-und-Herrsche-Mentalität.
Die Beschreibung des Divide-and-Conquer-Algorithmus ist im wahrsten Sinne des Wortes leicht zu verstehen:
# 🎜 🎜#- Teilen:
Kleinere Probleme rekursiv lösen (stoppen, wenn die Abschlussschicht erreicht ist oder wenn sie gelöst werden kann)
# 🎜🎜 # Erobern: - Rekursive Lösung. Wenn das Problem klein genug ist, lösen Sie es direkt.
- Konstruieren Sie die Lösung des Unterproblems in das übergeordnete Klassenproblem
#🎜🎜 # Der allgemeine Divide-and-Conquer-Algorithmus wird im Text in zwei oder mehr rekursive Aufrufe zerlegt, und Unterklassenprobleme möchten im Allgemeinen nicht interagieren (beeinflussen sich nicht gegenseitig). Bei der Lösung eines Problems, das sehr groß und schwer direkt zu lösen ist, aber leicht zu lösen ist, wenn es klein ist und das Problem die anwendbaren Bedingungen des Divide-and-Conquer-Algorithmus erfüllt, kann der Divide-and-Conquer-Algorithmus verwendet werden .
Welche Bedingungen (Merkmale) müssen also erfüllt sein, damit Probleme mit dem Divide-and-Conquer-Algorithmus gelöst werden können? 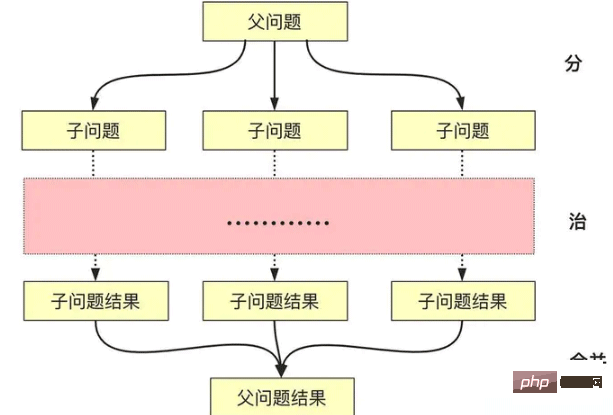 # 🎜🎜#
# 🎜🎜#
1 Das ursprüngliche Problem ist normalerweise relativ groß und schwer direkt zu lösen, kann aber leicht gelöst werden, wenn das Problem auf ein gewisses Maß reduziert wird.
- 2 . Das Problem kann mit der gleichen (ähnlichen) Lösungsmethode in mehrere kleinere Teilprobleme zerlegt werden. Und die Lösungen der Teilprobleme sind unabhängig und beeinflussen sich nicht gegenseitig.
- 3 Die Lösung des Problems kann durch Zusammenführen der durch das Problem zerlegten Teilprobleme erhalten werden.
- Sie fragen sich vielleicht, welche Beziehung zwischen dem Divide-and-Conquer-Algorithmus und der Rekursion besteht? Tatsächlich ist „Teile und herrsche“ ein wichtiger Gedanke, der sich auf den Prozess des Teilens, Eroberns und Verschmelzens von Problemen konzentriert. Rekursion ist eine Methode (ein Werkzeug), die Methoden verwendet, um sich selbst aufzurufen, um einen Hin- und Her-Prozess zu bilden, und Divide and Conquer kann mehrere solcher Hin- und Her-Prozesse nutzen.
3. Klassisches Problem des Divide-and-Conquer-Algorithmus
Für das klassische Problem des Divide-and-Conquer-Algorithmus ist seine Idee wichtig, da wir sie meistens verwenden Rekursion, um es zu implementieren, also in der Code-Implementierung Die meisten der oben genannten Punkte sind sehr einfach, und dieser Artikel konzentriert sich auch auf die Gedanken.
Das klassische Problem des Divide-and-Conquer-Algorithmus wird persönlich in zwei Kategorien unterteilt: Unterprobleme sind völlig unabhängig und Unterprobleme sind nicht völlig unabhängig.
1 Die Teilprobleme sind völlig unabhängig, was bedeutet, dass die Antwort auf die ursprüngliche Frage vollständig aus den Ergebnissen der Teilprobleme abgeleitet werden kann.
- 2. Die Teilprobleme sind möglicherweise nicht vollständig unabhängig Man muss bei der Betrachtung des Problems sorgfältig daraus lernen.
- 3.1. Binäre Suche
-
Binäre Suche ist ein Beispiel für „Teile und herrsche“, aber die binäre Suche hat ihre eigenen Besonderheiten
# 🎜🎜#
-
#🎜🎜 # Die normale Halbierung teilt ein vollständiges Intervall in zwei Intervalle. Die beiden Intervalle sollten den Wert separat ermitteln und dann das Ergebnis bestätigen. Das geordnete Intervall kann jedoch direkt bestimmen, in welchem Intervall sich das Ergebnis befindet, sodass nur eines der beiden geteilten Intervalle erforderlich ist Intervall berechnet und dann bis zum Ende fortgesetzt. Es gibt rekursive und nicht rekursive Implementierungsmethoden, aber nicht rekursive Methoden werden häufiger verwendet:
public int searchInsert(int[] nums, int target) { if(nums[0]>=target)return 0;//剪枝 if(nums[nums.length-1]==target)return nums.length-1;//剪枝 if(nums[nums.length-1]<target)return nums.length; int left=0,right=nums.length-1; while (left<right) { int mid=(left+right)/2; if(nums[mid]==target) return mid; else if (nums[mid]>target) { right=mid; } else { left=mid+1; } } return left; }3.2. Schnelle Sortierung
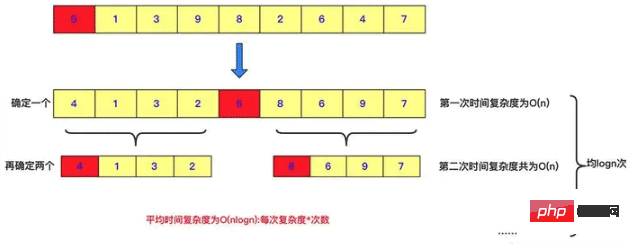
Schnelle Sortierung ist auch ein Beispiel für Teilen und Erobern. Bei jedem Durchlauf der schnellen Sortierung wird links eine Zahl ausgewählt, die kleiner als diese Zahl ist, und rechts eine Zahl, die größer als diese Zahl ist , und dann rekursiv dividieren und erobern, um das Problem zu lösen. Bei zwei Teilbereichen hat die schnelle Sortierung natürlich viel Arbeit geleistet. Wenn alle auf der untersten Ebene sortiert sind, ist der Wert dieser Sequenz der sortierte Wert. Dies ist eine Manifestation des Teilens und Herrschens.

public void quicksort(int [] a,int left,int right) { int low=left; int high=right; //下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!! if(low>high)//作为判断是否截止条件 return; int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。 while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。 { while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止 { high--; } //这样就找到第一个比它小的了 a[low]=a[high];//放到low位置 while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置 { low++; } a[high]=a[low]; } a[low]=k;//赋值然后左右递归分治求之 quicksort(a, left, low-1); quicksort(a, low+1, right); }3.3. Zusammenführungssortierung (umgekehrte Reihenfolge)
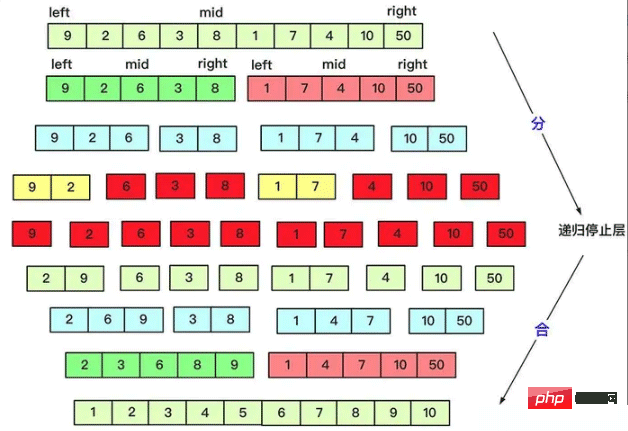
Schnellsortierung macht beim Teilen viel Arbeit, und beim Zusammenführen erfolgt die gleichmäßige Aufteilung entsprechend der Menge, während beim Zusammenführen dies bereits der Fall ist zwei mal zwei Der Reihe nach zusammenführen, da die erforderlichen Ergebnisse mit der Komplexität der Ebene O(n) zweier geordneter Sequenzen erzielt werden können. Die Verformung umgekehrter Ordnungszahlen basierend auf der Zusammenführungssortierung wird ebenfalls durch die Idee des Teilens und Eroberns gelöst. 3.4 Das Problem der maximalen Teilsequenzsumme ist beim Zusammenführen nicht dasselbe, da die Summe der Teilsequenzen ein Längenproblem mit sich bringt, sodass die korrekten Ergebnisse nicht unbedingt alle auf der linken oder rechten Seite liegen, aber die möglichen Ergebnisse sind:
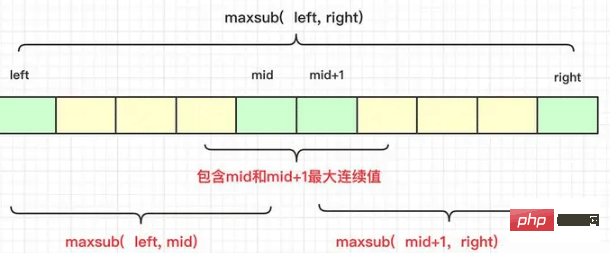
komplett auf der linken Seite die Mitte Komplett auf der rechten Seite der Mitte
- Eine Sequenz, die die beiden Knoten links und rechts der Mitte enthält
- kann in einem Bild ausgedrückt werden als:
Bei einer konkreten Betrachtung ist es daher notwendig, die Möglichkeit einer Rekursion auszuschließen. Das Ergebnis der Maximalwertzeichenfolge in der Mitte des erhaltenen Ergebnisses wird ebenfalls berechnet, um am Vergleich zwischen der linken und rechten Seite teilzunehmen.
Der für die maximale Teilsequenzsumme implementierte Code lautet:
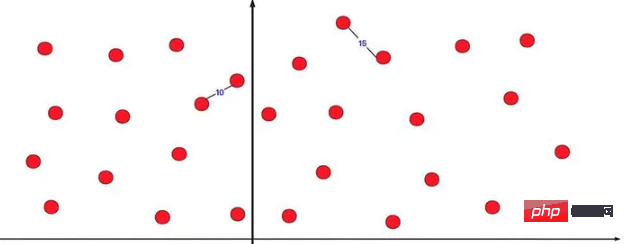
private static void mergesort(int[] array, int left, int right) { int mid=(left+right)/2; if(left<right) { mergesort(array, left, mid); mergesort(array, mid+1, right); merge(array, left,mid, right); } } private static void merge(int[] array, int l, int mid, int r) { int lindex=l;int rindex=mid+1; int team[]=new int[r-l+1]; int teamindex=0; while (lindex<=mid&&rindex<=r) {//先左右比较合并 if(array[lindex]<=array[rindex]) { team[teamindex++]=array[lindex++]; } else { team[teamindex++]=array[rindex++]; } } while(lindex<=mid)//当一个越界后剩余按序列添加即可 { team[teamindex++]=array[lindex++]; } while(rindex<=r) { team[teamindex++]=array[rindex++]; } for(int i=0;i<teamindex;i++) { array[l+i]=team[i]; } }3.5. Das nächstgelegene Punktpaar ist eine der sehr erfolgreichen Anwendungen von Teilen und Erobern. Auf der zweidimensionalen Koordinatenachse gibt es mehrere Punktkoordinaten, mit denen Sie den Abstand zwischen den beiden nächstgelegenen Punkten ermitteln können. Wenn Sie aufgefordert werden, ihn direkt zu ermitteln, ist die Aufzählung von Gewalt ein sehr, sehr großer Berechnungsaufwand Teile-und-herrsche-Methode zur Optimierung dieser Art von Problem.Wenn Sie es direkt in zwei Teile teilen und die Divide-and-Conquer-Berechnung durchführen, werden Sie auf jeden Fall feststellen, dass es ein Problem gibt, wenn der kürzeste Teil links und einer rechts liegt. Wir können es optimieren.
Berücksichtigen Sie im spezifischen Optimierungsplan die x- oder y-Dimension, teilen Sie die Daten in zwei Bereiche auf und berechnen Sie zunächst (nach derselben Methode) die kürzesten Punktpaare im linken bzw. rechten Bereich. Decken Sie es dann entsprechend dem kürzeren Abstand zwischen den beiden nach links und rechts ab, berechnen Sie den Abstand zwischen den abgedeckten linken und rechten Punkten, ermitteln Sie den kleinsten Abstand und vergleichen Sie ihn mit dem aktuell kürzesten Abstand.
Auf diese Weise können Sie viele Berechnungen einsparen. Auf diese Weise können Sie feststellen, dass bei dieser einmaligen Operation (unabhängig von Unterfällen) der rote Punkt auf der linken Seite die Entfernungsberechnung vermeidet, während die meisten roten Punkte auf der rechten Seite liegen (Zeitkomplexität von O). (n2)). Tatsächlich führt es bei der Durchführung interner Berechnungen im linken und rechten Intervall tatsächlich viele Divide-and-Conquer-Berechnungen rekursiv durch. Wie im Bild zu sehen ist:
Auf diese Weise können Sie feststellen, dass bei dieser einmaligen Operation (unabhängig von Unterfällen) der rote Punkt auf der linken Seite die Entfernungsberechnung vermeidet, während die meisten roten Punkte auf der rechten Seite liegen (Zeitkomplexität von O). (n2)). Tatsächlich führt es bei der Durchführung interner Berechnungen im linken und rechten Intervall tatsächlich viele Divide-and-Conquer-Berechnungen rekursiv durch. Wie im Bild zu sehen ist:
ac lautet: Allerdings gibt es bei dieser Art des Teilens und Herrschens ein Problem: Wenn die zweidimensionalen Koordinatenpunkte alle auf einer bestimmten Methode und auf einer bestimmten Achse gesammelt werden, ist der Effekt möglicherweise nicht offensichtlich (die Punkte liegen alle nahe beieinander). x=2 und haben wenig Einfluss auf die x-Division. Es ist notwendig, darauf zu achten. Der Code für
Allerdings gibt es bei dieser Art des Teilens und Herrschens ein Problem: Wenn die zweidimensionalen Koordinatenpunkte alle auf einer bestimmten Methode und auf einer bestimmten Achse gesammelt werden, ist der Effekt möglicherweise nicht offensichtlich (die Punkte liegen alle nahe beieinander). x=2 und haben wenig Einfluss auf die x-Division. Es ist notwendig, darauf zu achten. Der Code für 
public int maxSubArray(int[] nums) { int max=maxsub(nums,0,nums.length-1); return max; } int maxsub(int nums[],int left,int right) { if(left==right) return nums[left]; int mid=(left+right)/2; int leftmax=maxsub(nums,left,mid);//左侧最大 int rightmax=maxsub(nums,mid+1,right);//右侧最大 int midleft=nums[mid];//中间往左 int midright=nums[mid+1];//中间往右 int team=0; for(int i=mid;i>=left;i--) { team+=nums[i]; if(team>midleft) midleft=team; } team=0; for(int i=mid+1;i<=right;i++) { team+=nums[i]; if(team>midright) midright=team; } int max=midleft+midright;//中间的最大值 if(max<leftmax) max=leftmax; if(max<rightmax) max=rightmax; return max; }
Das obige ist der detaillierte Inhalt vonDesign und Analyse von Java-Algorithmen: Detaillierte Erläuterung von Beispielen für Divide-and-Conquer-Algorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!


 Auf diese Weise können Sie feststellen, dass bei dieser einmaligen Operation (unabhängig von Unterfällen) der rote Punkt auf der linken Seite die Entfernungsberechnung vermeidet, während die meisten roten Punkte auf der rechten Seite liegen (Zeitkomplexität von O). (n2)). Tatsächlich führt es bei der Durchführung interner Berechnungen im linken und rechten Intervall tatsächlich viele Divide-and-Conquer-Berechnungen rekursiv durch. Wie im Bild zu sehen ist:
Auf diese Weise können Sie feststellen, dass bei dieser einmaligen Operation (unabhängig von Unterfällen) der rote Punkt auf der linken Seite die Entfernungsberechnung vermeidet, während die meisten roten Punkte auf der rechten Seite liegen (Zeitkomplexität von O). (n2)). Tatsächlich führt es bei der Durchführung interner Berechnungen im linken und rechten Intervall tatsächlich viele Divide-and-Conquer-Berechnungen rekursiv durch. Wie im Bild zu sehen ist: 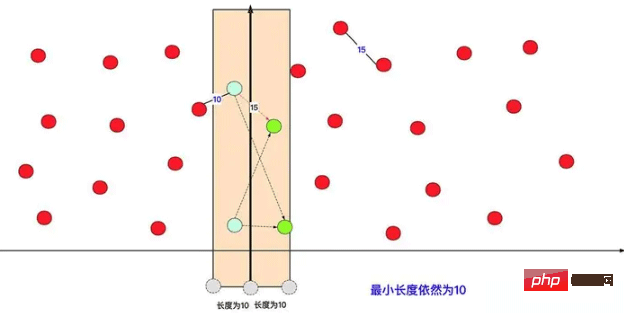 Allerdings gibt es bei dieser Art des Teilens und Herrschens ein Problem: Wenn die zweidimensionalen Koordinatenpunkte alle auf einer bestimmten Methode und auf einer bestimmten Achse gesammelt werden, ist der Effekt möglicherweise nicht offensichtlich (die Punkte liegen alle nahe beieinander). x=2 und haben wenig Einfluss auf die x-Division. Es ist notwendig, darauf zu achten. Der Code für
Allerdings gibt es bei dieser Art des Teilens und Herrschens ein Problem: Wenn die zweidimensionalen Koordinatenpunkte alle auf einer bestimmten Methode und auf einer bestimmten Achse gesammelt werden, ist der Effekt möglicherweise nicht offensichtlich (die Punkte liegen alle nahe beieinander). x=2 und haben wenig Einfluss auf die x-Division. Es ist notwendig, darauf zu achten. Der Code für