Wie verwende ich Heap, um das Top-k-Problem in Java zu lösen?

1. Was ist ein Haufen?

Heap-Struktur

Heap ist eigentlich eine Art Binärbaum, aber gewöhnliche Binärbäume speichern Daten in einer Kettenstruktur, während Heaps Daten sequentiell in Arrays speichern. Welche Art von Binärbaum eignet sich also für die sequentielle Speicherung?

Wir gehen davon aus, dass ein gewöhnlicher Binärbaum in einem Array gespeichert werden kann, dann können wir die folgende Struktur erhalten:

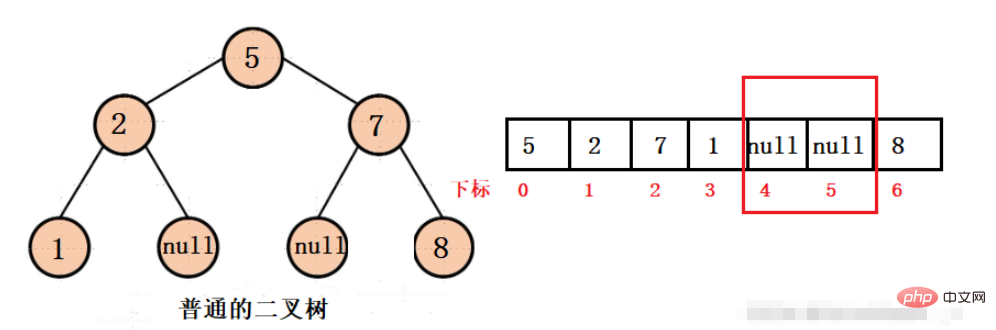
Wir können sehen, dass der Speicherplatz leer ist, wenn in der Mitte des Binärbaums ein Nullwert vorhanden ist des Arrays wird verschwendet. Was passiert also, damit der Platz nicht verschwendet wird? Das ist ein vollständiger Binärbaum.

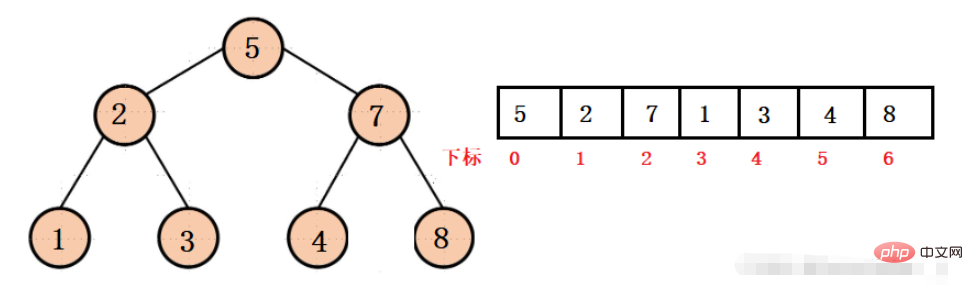
Aus der obigen Struktur können wir den Zeiger der Kettenstruktur nicht verwenden, um auf den untergeordneten Knoten oder den übergeordneten Knoten zuzugreifen. Wir können nur über den entsprechenden Index darauf zugreifen, was eigentlich relativ einfach ist.

Zum Beispiel im Bild unten:

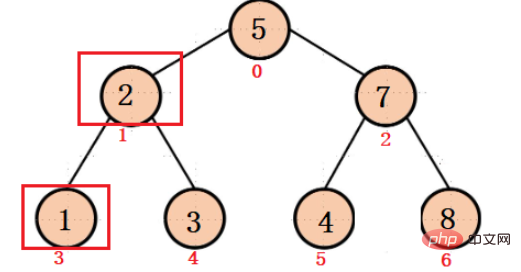
Es ist bekannt, dass der Index von 2 Knoten 1 ist, dann

Der Index seines linken Kindes ist: 2 * 2 + 1 = 3

Der Index seines rechten Kindes ist: 2 * 2 + 2 = 4

Im Gegenteil, es ist bekannt, dass der Index des 1-Knotens 3 und der Index des 3-Knotens 4 ist, also ist der Index des übergeordneten Knotens des

1-Knotens ist: (3 - 1) / 2 = 1

3 Knoten Der Index des übergeordneten Knotens ist: (4 - 1) / 2 = 1

Großer Root-Heap vs. kleiner Root-Heap

Großer Root-Heap (maximaler Heap). )

Der große Wurzelheap garantiert, dass der Wurzelknoten jedes Binärbaums größer ist als der linke und rechte Unterknoten

beginnt sich vom Wurzelknoten des letzten Teilbaums an den Wurzelknoten jedes Teilbaums anzupassen, sodass jeder Der Teilbaum wird nach unten zu einem großen Root-Heap angepasst und führt schließlich die endgültige Anpassung nach unten durch, um sicherzustellen, dass der gesamte Binärbaum ein großer Root-Heap ist (diese Anpassung dient hauptsächlich der späteren Heap-Sortierung).

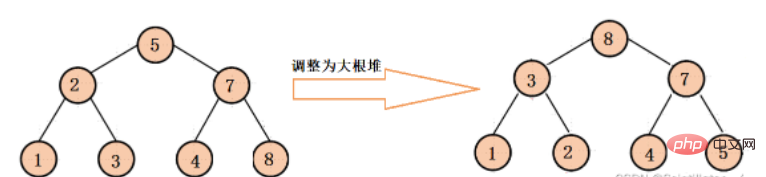
Der spezifische Anpassungsprozess ist wie folgt:

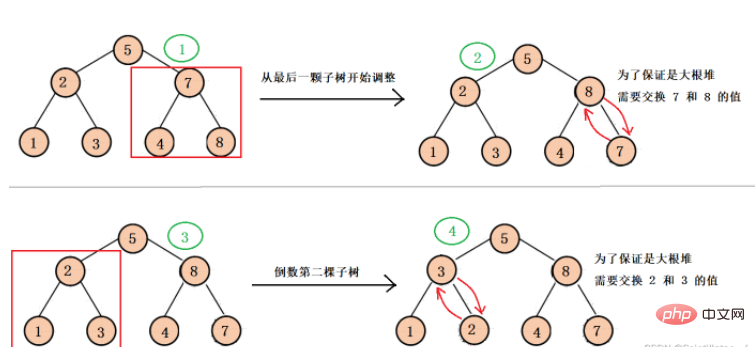
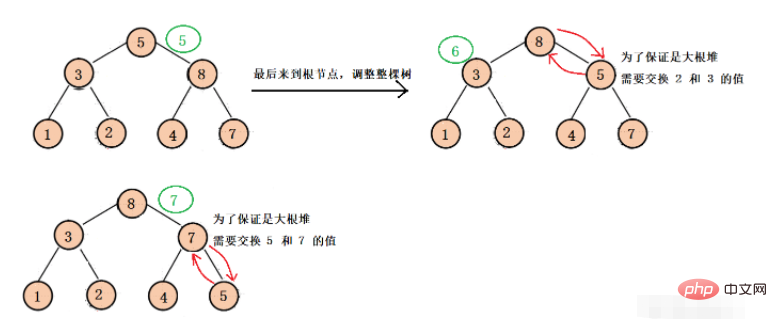
Wie implementiert man ihn mit Code?

Wir passen zuerst den letzten Teilbaum an und müssen dann den übergeordneten Wurzelknoten des letzten Teilbaums ermitteln. Wir wissen, dass der letzte Knotenindex des Arrays len - 1 ist und dieser Knoten das linke untergeordnete Element des letzten Teilbaums ist Oder das richtige Kind, entsprechend dem untergeordneten Index können Sie den Wurzelknoten-Index (übergeordnetes Element) erhalten, übergeordnetes Element – ​​Sie können jeden Unterbaum anpassen, bis Sie den Wurzelknoten erreichen, und dann zum letzten Mal nach unten anpassen, Sie können Big erhalten Haufen Wurzeln.

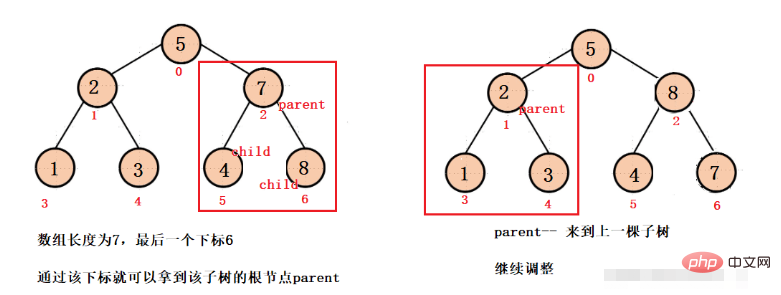
// 将数组变成大根堆结构
public void createHeap(int[] arr){
    for (int i = 0; i < arr.length; i++) {
        elem[i] = arr[i];// 放入elem[],假设不需要扩容
        usedSize++;
    }
    // 得到根节点parent, parent--依次来到每颗子树的根节点，
    for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
        // 依次向下搜索，使得每颗子树都变成大根堆
        shiftDown(parent,usedSize);
    }
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
    int child = parent*2+1;// 拿到左孩子
    while (child < len){
        // 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较 
        if (child+1 < len && (elem[child] < elem[child+1])){
            child++;
        }
        // 比较较大的孩子和父节点,看是否要交换
        int max = elem[parent] >= elem[child] ? parent : child;
        if (max == parent) break;// 如果不需要调整了，说明当前子树已经是大根堆了，直接 break
        swap(elem,parent,child);
        parent = child;// 继续向下检测，看是否要调整
        child = parent*2+1;
    }
}
public void swap(int[] arr,int i,int j){
  	int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

Kleiner Root-Heap (minimaler Heap)

Kleiner Root-Heap stellt sicher, dass der Wurzelknoten jedes Binärbaums kleiner ist als der linke und rechte untergeordnete Knoten

Der Anpassungsprozess ist der gleiche wie oben.

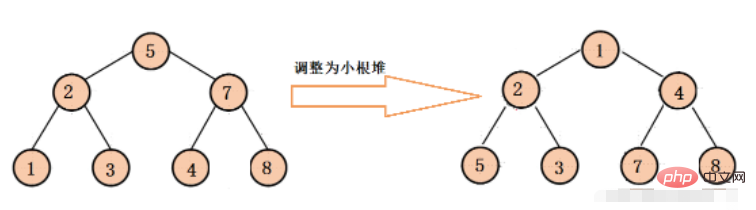
Prioritätswarteschlange (PriorityQueue)

In Java wird eine Heap-Datenstruktur (PriorityQueue) bereitgestellt, die auch als Prioritätswarteschlange bezeichnet wird. Wir erhalten ein Objekt ohne hinzugefügte Daten. Wir können hinzufügen oder Jedes Mal, wenn wir ein Element löschen oder hinzufügen, nimmt das System eine Gesamtanpassung vor und passt es wieder an einen kleinen Root-Heap an.

// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2，剩余最小的元素就是11，会被调整到堆顶，下一次弹出
System.out.println(smallHeap.poll());// 弹出11

 // 如果需要得到大根堆，在里面传一个比较器
 PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
     @Override
     public int compare(Integer o1, Integer o2) {
         return o2 - o1;
     }
 });

2. Ideen zur Lösung von Top-K-Problemen

Beispiel: Es gibt eine Reihe von Elementen und Sie werden gebeten, die ersten drei kleinsten Elemente zu finden.

Idee 1: Sortieren Sie das Array von klein nach groß und erhalten Sie die ersten 3 Elemente des Arrays. Es kann jedoch festgestellt werden, dass die zeitliche Komplexität dieser Methode zu hoch ist und nicht ratsam ist.

Idee 2: Platzieren Sie alle Elemente in einer Heap-Struktur und öffnen Sie dann drei Elemente. Jedes Popup-Element ist das kleinste im aktuellen Heap, und die drei Elemente, die angezeigt werden, sind die drei kleinsten Elemente in der Vergangenheit.

Diese Idee kann umgesetzt werden, aber wenn ich davon ausgehe, dass ich 1.000.000 Elemente habe und nur die ersten drei kleinsten Elemente aufrufe, dann wird ein Heap der Größe 1.000.000 verwendet. Die räumliche Komplexität hierfür ist zu hoch, daher wird diese Methode nicht empfohlen.

Drei Ideen:

Wir müssen die drei kleinsten Elemente erhalten und dann einen Heap mit einer Größe von 3 erstellen. Angenommen, die aktuelle Heap-Struktur ist genau mit 3 Elementen gefüllt, dann sind diese drei Elemente die aktuell kleinsten drei Elemente. Elemente. Angenommen, das vierte Element ist eines der von uns gewünschten Elemente, dann ist mindestens eines der ersten drei Elemente nicht das, was wir wollen, und es muss angezeigt werden.

Was wir erhalten möchten, sind die ersten drei kleinsten Elemente. Das größte Element in der aktuellen Heap-Struktur darf also nicht das sein, was wir wollen. Deshalb erstellen wir hier einen großen Root-Heap. Öffnen Sie das Element und fügen Sie dann das vierte Element ein, bis das gesamte Array durchlaufen ist.

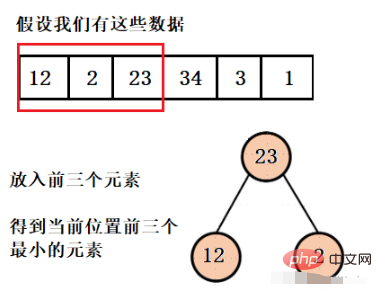
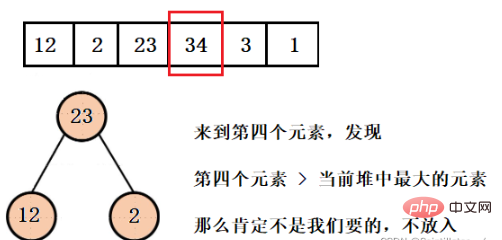
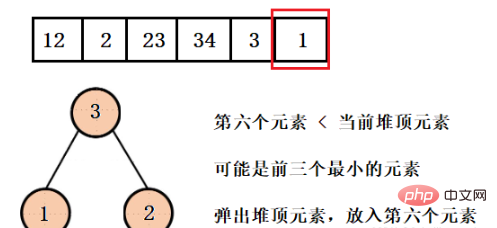
这样我们就得到了只含有前三个最小元素的堆，并且可以看到堆的大小一直都是3，而不是有多少数据就建多大的堆，然后再依次弹出元素就行了。

// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
     // 创建一个大小为 k的大根堆
     PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
         @Override
         public int compare(Integer o1, Integer o2) {
             return o2 - o1;
         }
     });
     for (int i = 0; i < arr.length; i++) {
         if (i < k){
             // 放入前 k 个元素
             maxHeap.offer(arr[i]);
         }else{
             // 从第 k+1个元素开始进行判断是否要入堆
             if (maxHeap.peek() > arr[i]){
                 maxHeap.poll();
                 maxHeap.offer(arr[i]);
             }
         }
     }
     int[] ret = new int[k];
     for (int i = 0; i < k; i++) {
         ret[i] = maxHeap.poll();
     }
     return ret;
 }

Das obige ist der detaillierte Inhalt vonWie verwende ich Heap, um das Top-k-Problem in Java zu lösen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!