Heim >Java >javaLernprogramm >So implementieren Sie den Java-Stack und die Java-Warteschlange
So implementieren Sie den Java-Stack und die Java-Warteschlange
- PHPznach vorne
- 2023-04-20 10:43:061255Durchsuche
1. Implementieren Sie eine kreisförmige Warteschlange
[OJ-Link]
Die kreisförmige Warteschlange verwendet im Allgemeinen eine Array erreichen. Wir müssen mehrere Probleme lösen.
(1) Array-Index implementiert Schleife
a Der Index steht zuletzt und weiter hinten (Offset ist kleiner als array.length): index = (index + offset) %. Array-Länge. Einfacher ausgedrückt: Wenn die Größe unseres Arrays 8 beträgt und der Index 7 erreicht, wie wir später auf 0 zurückkehren, können wir dies durch (Index + 1)% 8 erreichen.
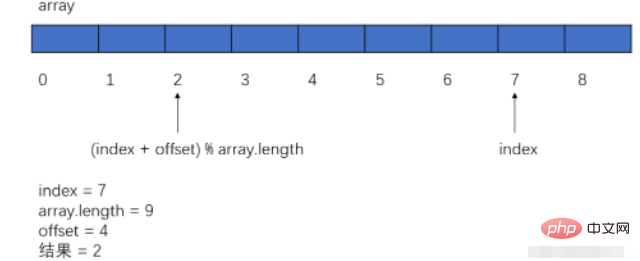
b Wenn der Index am weitesten vorne ist, treffen wir eine besondere Beurteilung und setzen ihn auf die Array-Größe minus eins.
(2) Unterscheiden Sie zwischen vollen und leeren Warteschlangen
Wir können eine Position für das Array reservieren, wenn hinten + 1 = vorne = vorne, was anzeigt, dass die Warteschlange leer ist. In diesem Fall müssen wir die Warteschlangengröße berücksichtigen, wenn wir die Array-Größe definieren. Sie muss um eins größer sein als die ursprüngliche.
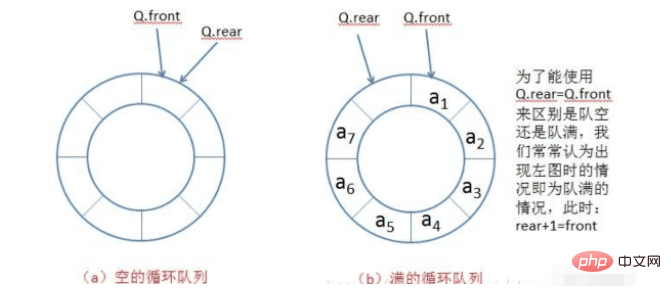
[Der Code lautet wie folgt]
class MyCircularQueue {
public int front;
public int rear;
public int[] array;
//构造方法
public MyCircularQueue(int k) {
//因为预留位置的缘故,数组的大小要定义为k+1
this.array=new int[k+1];
}
//入队
public boolean enQueue(int value) {
if(isFull()){
return false;
}
this.array[this.rear]=value;
this.rear=(this.rear+1)%this.array.length;
return true;
}
//出队
public boolean deQueue() {
if(isEmpty()){
return false;
}
this.front=(this.front+1)%this.array.length;
return true;
}
//获取队头
public int Front() {
if(isEmpty()){
return -1;
}
return this.array[front];
}
//获取队尾
public int Rear() {
if(isEmpty()){
return -1;
}
int index=-1;
if(this.rear==0){
index=this.array.length-1;
}else{
index=this.rear-1;
}
return this.array[index];
}
//判断是否为空
public boolean isEmpty() {
if(this.front==this.rear){
return true;
}
return false;
}
//判断队列是否满
public boolean isFull() {
if((this.rear+1)%this.array.length==this.front){
return true;
}
return false;
}
}2. Warteschlangenimplementierungsstapel
[ OJ-Link]
Aufgrund des First-in-Last-out-Prinzips des Stapels und des First-in-First-out-Prinzips der Warteschlange. Wir benötigen zwei Warteschlangen, um den Stapel zu implementieren. Wenn beide Warteschlangen leer sind, ist der Stapel leer.
Push: Es spielt keine Rolle, ob Sie zum ersten Mal in die Warteschlange gehen. Sie können beim Pushen einfach eine beliebige Warteschlange auswählen Zum Stapel später wird es definitiv eine Warteschlange geben, die nicht leer ist, und den Enqueue-Vorgang ausführen.
Pop: Wenn der Stapel zuerst leer ist, kann der Pop-Vorgang nicht ausgeführt werden. Wenn der Stapel nicht leer ist, muss eine leere Warteschlange vorhanden sein (Warteschlange1). . Wenn eine Warteschlange nicht leer ist (Warteschlange2), fügen Sie Elemente der Größe 1 in Warteschlange1 in Warteschlange2 ein (beachten Sie insbesondere, dass die Funktion zum Ermitteln der Größe von Warteschlange1 nicht in eine Schleife eingefügt werden kann. Wenn die Warteschlange aus der Warteschlange entfernt wird, ändert sich ihre Größe.) und schließlich das letzte Element in queue1 als Rückgabewert aus der Warteschlange entfernen.
-
Das oberste Element des Stapels abrufen (oben): Es ist fast dasselbe wie das Öffnen des Stapels, daher werde ich nicht auf Details eingehen
#🎜 🎜#
class MyStack {
private Queue<Integer> queue1;
private Queue<Integer> queue2;
//构造方法
public MyStack() {
queue1=new LinkedList<>();
queue2=new LinkedList<>();
}
//入栈
public void push(int x) {
if(!queue2.isEmpty()){
queue2.offer(x);
}else{
queue1.offer(x);
}
}
//出栈
public int pop() {
if(empty()){
return -1;
}
if(queue1.isEmpty()){
int size=queue2.size();
for(int i=0;i<size-1;++i){
int x=queue2.poll();
queue1.offer(x);
}
return queue2.poll();
}else{
int size=queue1.size();
for(int i=0;i<size-1;++i){
int x=queue1.poll();
queue2.offer(x);
}
return queue1.poll();
}
}
//获取栈顶元素
public int top() {
if(empty()){
return -1;
}
if(queue1.isEmpty()){
int x=-1;
int size=queue2.size();
for(int i=0;i<size;++i){
x=queue2.poll();
queue1.offer(x);
}
return x;
}else{
int size=queue1.size();
int x=-1;
for(int i=0;i<size;++i){
x=queue1.poll();
queue2.offer(x);
}
return x;
}
}
//判断栈是否为空
public boolean empty() {
if(queue1.isEmpty()&&queue2.isEmpty()){
return true;
}
return false;
}
}3. Stack-Implementierungswarteschlange [OJ-Link] #🎜🎜 # Es ist immer noch dasselbe wie oben, es werden zwei Stapel benötigt (Stack1, Stack2). Anders als bei der Implementierung der Stapelwarteschlange kann das Einreihen in die Warteschlange nur auf demselben Stapel ausgeführt werden. Wenn beide Stapel leer sind, ist die Warteschlange leer.
- Team betreten (Push): Es wird angegeben, dass Stack1 zum Beitritt zum Team verwendet wird. Jedes Mal, wenn Sie der Warteschlange beitreten, schieben Sie einfach stack1 in den Stack.
- Aus der Warteschlange entfernen (Pop): Erfordert Stack2, um den Vorgang zum Entfernen aus der Warteschlange durchzuführen. Wenn die Warteschlange leer ist, kann der Vorgang zum Entfernen aus der Warteschlange nicht ausgeführt werden. Wenn Stapel2 leer ist, müssen wir alle Elemente in Stapel1 in Stapel2 einfügen und dann Stapel2 entfernen. Wenn Stapel2 nicht leer ist, öffnen Sie Stapel2 einfach direkt.
- Holen Sie sich das Anfangselement der Warteschlange (Peek): Es ist dasselbe wie die Pop-Operation. Am Ende müssen Sie nur das oberste Element von Stack2 abrufen .
- [Der Code lautet wie folgt]
class MyQueue {
private Stack<Integer> stack1;
private Stack<Integer> stack2;
//构造方法
public MyQueue() {
stack1=new Stack<>();
stack2=new Stack<>();
}
//入队操作
public void push(int x) {
stack1.push(x);
}
//出队操作
public int pop() {
if(stack2.empty()){
int size=stack1.size();
for(int i=0;i<size;++i){
int x=stack1.pop();
stack2.push(x);
}
}
return stack2.pop();
}
//获取队列开头的元素
public int peek() {
if(stack2.empty()){
int size=stack1.size();
for(int i=0;i<size;++i){
int x=stack1.pop();
stack2.push(x);
}
}
return stack2.peek();
}
//判断队列是否为空
public boolean empty() {
if(stack1.empty()&&stack2.empty()){
return true;
}
return false;
}
}4. Implementieren Sie den Mindeststapel
[OJ-Link]
Tatsächlich ist es notwendig, das kleinste Element des Stapels innerhalb der zeitlichen Komplexität von O(1) zu finden. Zur Implementierung sind zwei Stapel erforderlich, und ein Stapel wird für Popp- und Push-Vorgänge verwendet. Stellen Sie einfach sicher, dass das oberste Element des anderen Stapels unabhängig von Ihrer Vorgehensweise das kleinste Element des aktuellen Stapels ist.
Es gibt zwei Stapel, Stapel1 und Stapel2, und die Operationen der Station befinden sich alle in Stapel1:
- In den Stapel schieben: Wenn ja Wird zum ersten Mal in den Stapel geschoben, müssen wir es in Stapel2 legen und dann auf den Stapel schieben. Vergleichen Sie das geschobene Element mit dem obersten Element von Stapel2 in Stack2.
- Pop: Wenn Stack1 geöffnet wird, wird es mit dem obersten Element von Stack2 verglichen, wenn es mit dem obersten Element von Stack2 übereinstimmt.
- Dadurch wird sichergestellt, dass das oberste Element von Stack2 immer das kleinste Element von Stack1 ist. Hinweis: Wenn in Stapel1 zwei identische Mindestelemente in den Stapel geschoben werden, muss Stapel2 in den Stapel geschoben werden.
【Code lautet wie folgt】
class MinStack {
private Stack<Integer> stack1;
private Stack<Integer> stack2;
//构造方法
public MinStack() {
stack1=new Stack<>();
stack2=new Stack<>();
}
//入栈
public void push(int val) {
stack1.push(val);
if(stack2.empty()){
stack2.push(val);
}else{
if(val<=stack2.peek()){
stack2.push(val);
}
}
}
//出栈
public void pop() {
int x=stack1.pop();
if(x==stack2.peek()){
stack2.pop();
}
}
//获取栈顶元素
public int top() {
return stack1.peek();
}
//获取栈的最小元素
public int getMin() {
return stack2.peek();
}
}Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Java-Stack und die Java-Warteschlange. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

