So implementieren Sie einen genetischen Algorithmus mit Python

遗传算法 ist eine stochastische globale Such- und Optimierungsmethode, die durch Nachahmung des biologischen Evolutionsmechanismus in der Natur entwickelt wurde. Sie basiert auf Darwins Evolutionstheorie und Mendels Genetiktheorie. Sein Kern ist eine effiziente, parallele, globale Suchmethode, die während des Suchprozesses automatisch Wissen über den Suchraum erfassen und akkumulieren und den Suchprozess adaptiv steuern kann, um die optimale Lösung zu erhalten. Genetische Algorithmusoperationen nutzen das Prinzip des Überlebens des Stärkeren, um in jeder Generation des genetischen Algorithmus sukzessive eine nahezu optimale Lösung in der potenziellen Lösungspopulation zu generieren, entsprechend dem Fitnesswert des Individuums in der Problemdomäne und aus der natürlichen Genetik Für die individuelle Auswahl wird eine der chinesischen Literatur entlehnte Rekonstruktionsmethode verwendet, um eine neue Näherungslösung zu generieren. Dieser Prozess führt zur Evolution von Individuen in der Population, und die daraus resultierenden neuen Individuen sind, genau wie Veränderungen in der Natur, anpassungsfähiger an die Umwelt als die ursprünglichen Individuen.

Spezifische Schritte des genetischen Algorithmus:

(1) Initialisierung: Setzen Sie den Evolutionsgenerationszähler auf t=0, legen Sie die maximale Evolutionsgeneration T, die Crossover-Wahrscheinlichkeit und die Mutationswahrscheinlichkeit fest und generieren Sie zufällig M Individuen als Anfangspopulation P

(2) Einzelbewertung: Berechnen Sie die Fitness jedes Einzelnen in der Population P

(3) Auswahloperation: Wenden Sie den Auswahloperator auf die Population an. Basierend auf der individuellen Fitness wird das optimale Individuum ausgewählt, um es direkt an die nächste Generation zu vererben, oder es werden neue Individuen durch paarweise Überkreuzung generiert und dann an die nächste Generation vererbt. (4) Crossover-Operation: Unter der Kontrolle der Crossover-Wahrscheinlichkeit werden zwei Individuen hergestellt in der Gruppe sind Kreuzen Sie die beiden

(5) Mutationsoperation: Unter der Kontrolle der Mutationswahrscheinlichkeit werden die Individuen in der Population mutiert, das heißt, die Gene eines bestimmten Individuums werden zufällig angepasst

(6) Nach der Auswahl, Crossover und Mutationsoperationen, wir erhalten die nächste Generationsgruppe P1.

Wiederholen Sie die obigen (1) bis (6), bis die genetische Generation T ist, verwenden Sie das Individuum mit der während des Evolutionsprozesses erhaltenen optimalen Fitness als optimale Lösungsausgabe und beenden Sie die Berechnung.

Traveling Salesman Problem (TSP): Es gibt n Städte. Ein Verkäufer muss von einer der Städte aus starten, alle Städte besuchen und dann in die Stadt zurückkehren, in der er begonnen hat, um den kürzesten Weg zu finden.

Bei der Anwendung des genetischen Algorithmus zur Lösung des TSP-Problems sind einige Konventionen erforderlich. Ein Gen ist eine Reihe von Stadtsequenzen, und die Fitness ist die Distanzsumme der Stadtsequenzen gemäß diesem Gen.

1.2 Experimenteller Code

import random
import math
import matplotlib.pyplot as plt
# 读取数据
f=open("test.txt")
data=f.readlines()
# 将cities初始化为字典，防止下面被当成列表
cities={}
for line in data:
    #原始数据以\n换行，将其替换掉
    line=line.replace("\n","")
    #最后一行以EOF为标志，如果读到就证明读完了，退出循环
    if(line=="EOF"):
        break
    #空格分割城市编号和城市的坐标
    city=line.split(" ")
    map(int,city)
    #将城市数据添加到cities中
    cities[eval(city[0])]=[eval(city[1]),eval(city[2])]
 
# 计算适应度，也就是距离分之一，这里用伪欧氏距离
def calcfit(gene):
    sum=0
    #最后要回到初始城市所以从-1，也就是最后一个城市绕一圈到最后一个城市
    for i in range(-1,len(gene)-1):
        nowcity=gene[i]
        nextcity=gene[i+1]
        nowloc=cities[nowcity]
        nextloc=cities[nextcity]
        sum+=math.sqrt(((nowloc[0]-nextloc[0])**2+(nowloc[1]-nextloc[1])**2)/10)
 
    return 1/sum
 
# 每个个体的类，方便根据基因计算适应度
class Person:
    def __init__(self,gene):
        self.gene=gene
        self.fit=calcfit(gene)
class Group:
    def __init__(self):
        self.GroupSize=100  #种群规模
        self.GeneSize=48    #基因数量，也就是城市数量
        self.initGroup()
        self.upDate()
    #初始化种群，随机生成若干个体
    def initGroup(self):
        self.group=[]
        i=0
        while(i<self.GroupSize):
            i+=1
            #gene如果在for以外生成只会shuffle一次
            gene=[i+1 for i in range(self.GeneSize)]
            random.shuffle(gene)
            tmpPerson=Person(gene)
            self.group.append(tmpPerson)
 
    #获取种群中适应度最高的个体
    def getBest(self):
        bestFit=self.group[0].fit
        best=self.group[0]
        for person in self.group:
            if(person.fit>bestFit):
                bestFit=person.fit
                best=person
        return best
    #计算种群中所有个体的平均距离
    def getAvg(self):
        sum=0
        for p in self.group:
            sum+=1/p.fit
        return sum/len(self.group)
    #根据适应度，使用轮盘赌返回一个个体，用于遗传交叉
    def getOne(self):
        #section的简称，区间
        sec=[0]
        sumsec=0
        for person in self.group:
            sumsec+=person.fit
            sec.append(sumsec)
        p=random.random()*sumsec
        for i in range(len(sec)):
            if(p>sec[i] and p<sec[i+1]):
                #这里注意区间是比个体多一个0的
                return self.group[i]
    #更新种群相关信息
    def upDate(self):
        self.best=self.getBest()
# 遗传算法的类，定义了遗传、交叉、变异等操作
class GA:
    def __init__(self):
        self.group=Group()
        self.pCross=0.35    #交叉率
        self.pChange=0.1    #变异率
        self.Gen=1  #代数
 
    #变异操作
    def change(self,gene):
        #把列表随机的一段取出然后再随机插入某个位置
        #length是取出基因的长度，postake是取出的位置，posins是插入的位置
        geneLenght=len(gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(0, geneLenght - 1)
        newGene = gene[:]       # 产生一个新的基因序列，以免变异的时候影响父种群
        newGene[index1], newGene[index2] = newGene[index2], newGene[index1]
        return newGene
 
    #交叉操作
    def cross(self,p1,p2):
        geneLenght=len(p1.gene)
        index1 = random.randint(0, geneLenght - 1)
        index2 = random.randint(index1, geneLenght - 1)
        tempGene = p2.gene[index1:index2]   # 交叉的基因片段
        newGene = []
        p1len = 0
        for g in p1.gene:
              if p1len == index1:
                    newGene.extend(tempGene)     # 插入基因片段
                    p1len += 1
              if g not in tempGene:
                    newGene.append(g)
                    p1len += 1
        return newGene
 
    #获取下一代
    def nextGen(self):
        self.Gen+=1
        #nextGen代表下一代的所有基因
        nextGen=[]
        #将最优秀的基因直接传递给下一代
        nextGen.append(self.group.getBest().gene[:])
        while(len(nextGen)<self.group.GroupSize):
            pChange=random.random()
            pCross=random.random()
            p1=self.group.getOne()
            if(pCross<self.pCross):
                p2=self.group.getOne()
                newGene=self.cross(p1,p2)
            else:
                newGene=p1.gene[:]
            if(pChange<self.pChange):
                newGene=self.change(newGene)
            nextGen.append(newGene)
        self.group.group=[]
        for gene in nextGen:
            self.group.group.append(Person(gene))
            self.group.upDate()
 
    #打印当前种群的最优个体信息
    def showBest(self):
        print("第{}代\t当前最优{}\t当前平均{}\t".format(self.Gen,1/self.group.getBest().fit,self.group.getAvg()))
 
    #n代表代数，遗传算法的入口
    def run(self,n):
        Gen=[]  #代数
        dist=[] #每一代的最优距离
        avgDist=[]  #每一代的平均距离
        #上面三个列表是为了画图
        i=1
        while(i<n):
            self.nextGen()
            self.showBest()
            i+=1
            Gen.append(i)
            dist.append(1/self.group.getBest().fit)
            avgDist.append(self.group.getAvg())
        #绘制进化曲线
        plt.plot(Gen,dist,&#39;-r&#39;)
        plt.plot(Gen,avgDist,&#39;-b&#39;)
        plt.show()
 
ga=GA()
ga.run(3000)
print("进行3000代后最优解：",1/ga.group.getBest().fit)

1.3 Experimentelle Ergebnisse

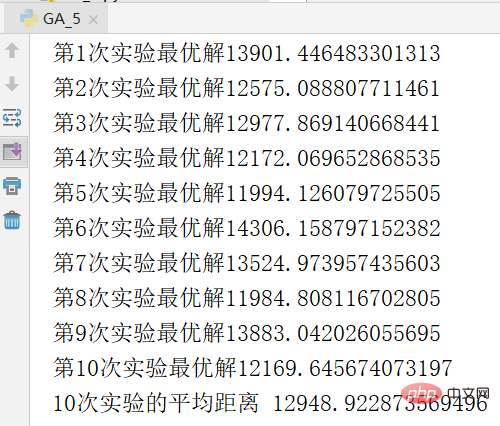
Das Bild unten ist ein Screenshot der Ergebnisse eines Experiments

Um die Eventualität des Experiments zu vermeiden, wurde das Experiment wiederholt 10 Mal und berechneter Durchschnitt, die Ergebnisse sind wie folgt.

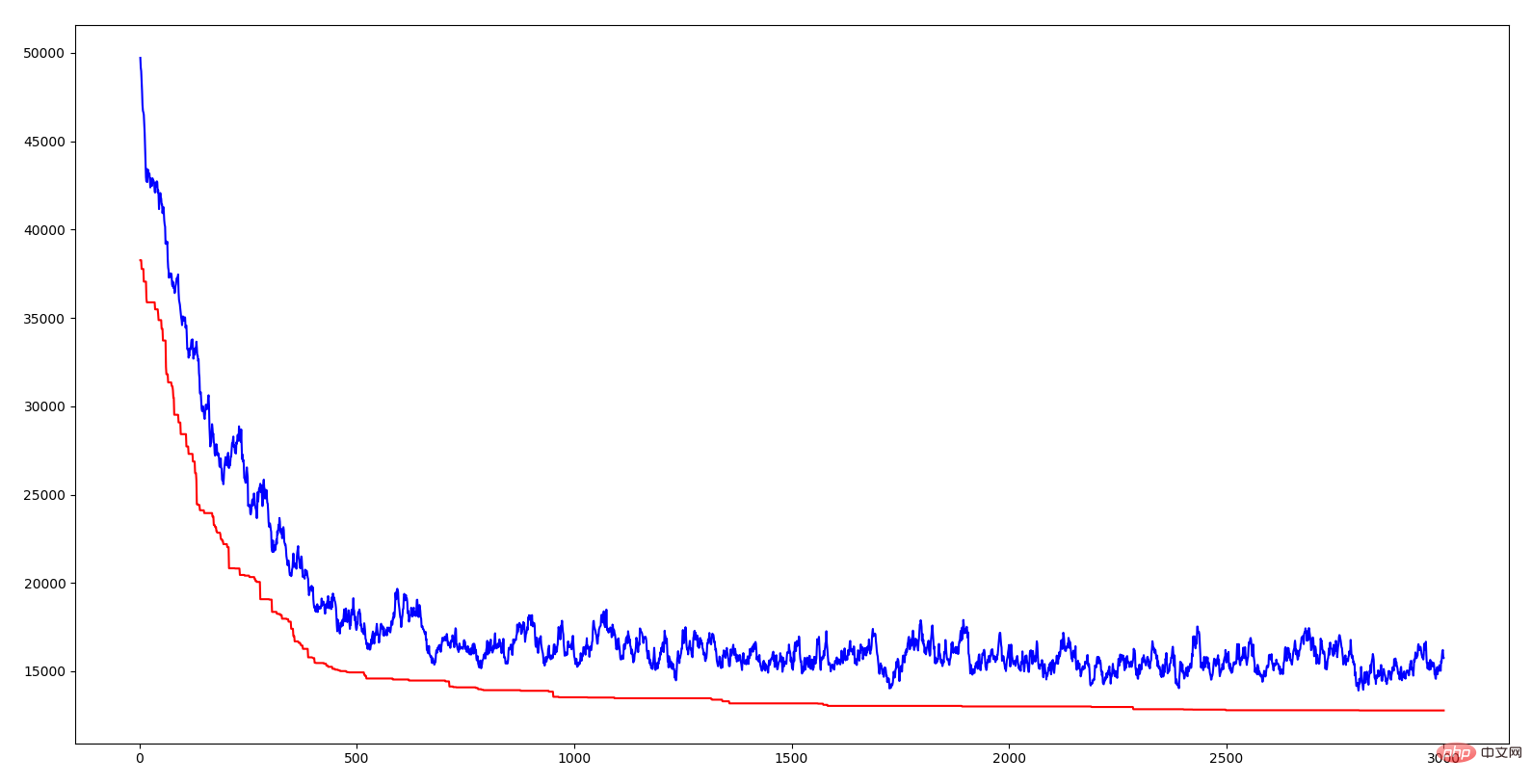Die Abszisse in der obigen Abbildung ist die Algebra, die Ordinate ist der Abstand, die rote Kurve ist der Abstand des optimalen Individuums jeder Generation und die blaue Kurve ist der durchschnittliche Abstand jeder Generation. Es ist zu erkennen, dass beide Linien einen Abwärtstrend aufweisen, was bedeutet, dass sie sich weiterentwickeln. Die Verringerung der durchschnittlichen Entfernung weist darauf hin, dass sich dieses hervorragende Merkmal aufgrund der Entstehung hervorragender Gene (d. h. einer bestimmten städtischen Sequenz) schnell auf die gesamte Bevölkerung ausbreitet. Genau wie in der Natur können nur diejenigen überleben, die über Gene verfügen, die sich an die Umwelt anpassen. Dementsprechend überleben diejenigen mit hervorragenden Genen. Die Bedeutung der Einführung von Crossover-Rate und Mutationsrate in den Algorithmus besteht darin, die aktuellen hervorragenden Gene sicherzustellen und zu versuchen, bessere Gene zu generieren. Wenn sich alle Individuen kreuzen, können einige hervorragende Gensegmente verloren gehen. Wenn sich keines kreuzt, können zwei hervorragende Gensegmente nicht zu besseren Genen kombiniert werden. Wenn es keine Variation gibt, können keine besser an die Umwelt angepassten Individuen erzeugt werden. Ich muss seufzen, dass die Weisheit der Natur so mächtig ist.

Das oben erwähnte Genfragment ist eine kurze Stadtsequenz in TSP. Wenn die Distanzsumme einer bestimmten Sequenz relativ klein ist, bedeutet dies, dass diese Sequenz eine relativ gute Durchlaufreihenfolge für diese Städte darstellt. Der genetische Algorithmus erreicht eine kontinuierliche Optimierung der TSP-Lösung durch die Kombination dieser hervorragenden Fragmente. Die Kombinationsmethode basiert auf der Weisheit der Natur, der Vererbung, der Mutation und dem Überleben des Stärksten.

1.4 Zusammenfassung des Experiments

1. Wie erreicht man das „Überleben des Stärkeren“ im Algorithmus?

Das sogenannte Survival of the Fittest bedeutet die Erhaltung hervorragender Gene und die Eliminierung von Genen, die nicht für die Umwelt geeignet sind. Im obigen GA-Algorithmus verwende ich Roulette, das heißt, im genetischen Schritt (ob Crossover oder nicht) wird jedes Individuum anhand seiner Fitness ausgewählt. Auf diese Weise können Personen mit hoher Fitness mehr Nachkommen bekommen und so das Ziel des Überlebens des Stärkeren erreichen.

Während des spezifischen Implementierungsprozesses habe ich beim ersten Screening von Personen im genetischen Schritt einen Fehler gemacht und diese Person jedes Mal aus der Gruppe gelöscht. Wenn ich jetzt darüber nachdenke, war dieser Ansatz sehr dumm. Obwohl ich damals bereits Roulette implementiert hatte, würde es dazu führen, dass jedes Individuum gleichermaßen Nachkommen zur Welt bringt. Das sogenannte Roulette ist nur ein Weg Lassen Sie diejenigen mit hoher Fitness zuerst vererben. Dieser Ansatz weicht völlig von der ursprünglichen Absicht des „survival of the fittest“ ab. Der richtige Ansatz besteht darin, Individuen zur Vererbung auszuwählen und sie dann wieder in die Population aufzunehmen. Dadurch kann sichergestellt werden, dass Individuen mit hoher Fitness mehrfach vererbt werden, mehr Nachkommen hervorbringen und gleichzeitig hervorragende Gene weiter verbreiten wird nur wenige Nachkommen hervorbringen oder direkt eliminiert werden.

2. Wie kann sichergestellt werden, dass die Entwicklung immer in eine positive Richtung verläuft?

Die sogenannte Vorwärtsprogression bedeutet, dass die optimalen Individuen der nächsten Generation mehr oder genauso anpassungsfähig an die Umwelt sein müssen wie die vorherige Generation. Die von mir angewandte Methode besteht darin, dass das optimale Individuum direkt in die nächste Generation übergeht, ohne an Operationen wie der Crossover-Mutation beteiligt zu sein. Dies kann verhindern, dass die umgekehrte Evolution aufgrund dieser Operationen die derzeit besten Gene „kontaminiert“.

Während des Implementierungsprozesses bin ich auch auf ein anderes Problem gestoßen, unabhängig davon, ob es durch die Übergabe als Referenz oder als Wert verursacht wurde. Eine Liste wird für die Überkreuzung und Mutation einzelner Gene verwendet. Bei der Übergabe der Liste in Python handelt es sich tatsächlich um eine Referenz. Dies führt dazu, dass die eigenen Gene der Person nach der Überkreuzung und Mutation geändert werden. Das Ergebnis ist eine sehr langsame Evolution, begleitet von einer umgekehrten Evolution.

3. Wie erreicht man Crossover?

Wählen Sie die Fragmente eines Individuums aus und fügen Sie sie in ein anderes Individuum ein, und platzieren Sie die nicht duplizierten Gene der Reihe nach an anderen Stellen.

Bei der Implementierung dieses Schritts habe ich diese Funktion aufgrund meines inhärenten Verständnisses für das Verhalten echter Chromosomen beim Studium der Biologie falsch implementiert: „Homologe Chromosomen kreuzen sich und tauschen homologe Segmente aus“. Ich habe nur die Fragmente der beiden Personen an derselben Position ausgetauscht, um die Überkreuzung zu vervollständigen. Offensichtlich ist dieser Ansatz falsch und wird zur Verdoppelung der Städte führen.

4. Als ich anfing, diesen Algorithmus zu schreiben, habe ich ihn halb OOP und halb prozessorientiert geschrieben.

Bei den anschließenden Tests stellte ich fest, dass es mühsam war, Parameter zu ändern und einzelne Informationen zu aktualisieren, also habe ich alles auf OOP geändert, was es viel bequemer machte. OOP bietet große Flexibilität und Einfachheit für die Simulation realer Probleme wie diesem.

5. Wie kann das Auftreten lokaler optimaler Lösungen verhindert werden?

Während des Testprozesses wurde festgestellt, dass gelegentlich lokale optimale Lösungen auftauchen, die sich über einen längeren Zeitraum nicht weiterentwickeln werden, und dass die Lösungen zu diesem Zeitpunkt weit von der optimalen Lösung entfernt sind. Obwohl es nahe an der optimalen Lösung liegt, ist es auch nach späteren Anpassungen immer noch ein „lokales Optimum“, da es die optimale Lösung noch nicht erreicht hat.

Der Algorithmus konvergiert am Anfang sehr schnell, wird aber im weiteren Verlauf immer langsamer oder bewegt sich überhaupt nicht mehr. Da im späteren Stadium alle Individuen relativ ähnliche hervorragende Gene haben, ist der Einfluss des Crossovers auf die Evolution zu diesem Zeitpunkt sehr schwach und die Hauptantriebskraft der Evolution wird zur Mutation, und Mutation ist ein gewalttätiger Algorithmus. Wenn Sie Glück haben, können Sie schnell zu einem besseren Individuum mutieren, aber wenn Sie kein Glück haben, müssen Sie warten.

Die Lösung zur Verhinderung lokaler optimaler Lösungen besteht darin, die Populationsgröße zu erhöhen, sodass es zu mehr individuellen Mutationen kommt und eine größere Wahrscheinlichkeit besteht, weiterentwickelte Individuen hervorzubringen. Der Nachteil einer Vergrößerung der Population besteht darin, dass die Berechnungszeit jeder Generation länger wird, was bedeutet, dass sich die beiden gegenseitig hemmen. Obwohl eine große Populationsgröße letztendlich lokale optimale Lösungen vermeiden kann, dauert es lange, bis jede Generation die optimale Lösung findet, während dies bei einer kleineren Populationsgröße nicht der Fall sein wird, obwohl die Berechnungszeit jeder Generation schnell ist nach mehreren Generationen gelöst wird, fällt in ein lokales Optimum.

Eine mögliche Optimierungsmethode besteht darin, in den frühen Stadien der Evolution eine kleinere Populationsgröße zu verwenden, um die Evolution zu beschleunigen. Wenn die Fitness einen bestimmten Schwellenwert erreicht, erhöhen Sie die Populationsgröße und die Mutationsrate, um die Entstehung lokal optimaler Lösungen zu vermeiden. . Diese dynamische Anpassungsmethode wird verwendet, um das Gleichgewicht zwischen der Recheneffizienz jeder Generation und der Gesamtrecheneffizienz abzuwägen.

Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen genetischen Algorithmus mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!