Verabschiedung! Python-Schleifen, Vektorisierung ist erstaunlich

Wir haben Schleifen in fast allen Programmiersprachen kennengelernt. Standardmäßig beginnen wir also bei jeder sich wiederholenden Operation mit der Implementierung von Schleifen. Aber wenn wir es mit vielen Iterationen (Millionen/Milliarden Zeilen) zu tun haben, ist die Verwendung von Schleifen eine echte Qual, und Sie könnten stundenlang stecken bleiben, nur um später festzustellen, dass es nicht funktioniert. An dieser Stelle wird die Implementierung der Vektorisierung in Python äußerst wichtig.

Was ist Vektorisierung?

Vektorisierung ist eine Technik zur Implementierung von (NumPy)-Array-Operationen an Datensätzen. Im Hintergrund werden alle Elemente des Arrays oder der Reihe gleichzeitig bearbeitet (im Gegensatz zu einer „for“-Schleife, die jeweils eine Zeile bearbeitet).

In diesem Blog werden wir uns einige Anwendungsfälle ansehen, bei denen wir Python-Schleifen einfach durch Vektorisierung ersetzen können. Dies wird Ihnen helfen, Zeit zu sparen und Ihre Kenntnisse im Programmieren zu verbessern.

Anwendungsfall 1: Ermitteln der Summe von Zahlen

Schauen wir uns zunächst ein einfaches Beispiel für das Ermitteln der Summe von Zahlen in Python mithilfe von Schleifen und Vektoren an.

Schleifen verwenden

import time 
start = time.time()

# 遍历之和
total = 0
# 遍历150万个数字
for item in range(0, 1500000):
total = total + item

print('sum is:' + str(total))
end = time.time()

print(end - start)

#1124999250000
#0.14 Seconds

Vektorisierung verwenden

import numpy as np

start = time.time()

# 向量化和--使用numpy进行向量化
# np.range创建从0到1499999的数字序列
print(np.sum(np.arange(1500000)))

end = time.time()
print(end - start)

##1124999250000
##0.008 Seconds

Die Ausführungszeit der Vektorisierung beträgt etwa das 18-fache im Vergleich zur Iteration mit Bereichsfunktionen. Dieser Unterschied wird bei der Arbeit mit Pandas DataFrame deutlicher.

Anwendungsfall 2: Mathematische DataFrame-Operationen

In der Datenwissenschaft verwenden Entwickler bei der Arbeit mit Pandas DataFrame Schleifen, um neue abgeleitete Spalten für mathematische Operationen zu erstellen.

Im Beispiel unten sehen wir, dass Schleifen in solchen Anwendungsfällen leicht durch Vektorisierung ersetzt werden können.

DataFrame erstellen

DataFrame sind tabellarische Daten in Form von Zeilen und Spalten.

Wir erstellen einen Pandas-DataFrame mit 5 Millionen Zeilen und 4 Spalten, gefüllt mit Zufallswerten zwischen 0 und 50.

import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randint(0, 50, 
size=(5000000, 4)),
columns=('a','b','c','d'))
df.shape
# (5000000, 5)
df.head()

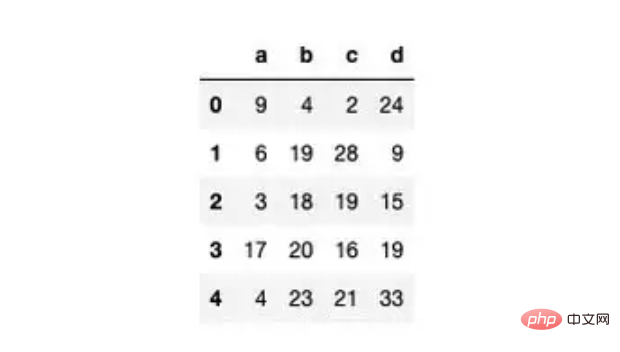
Wir erstellen eine neue Spalte „Verhältnis“, um das Verhältnis der Spalten „d“ und „c“ zu ermitteln.

Schleifen verwenden

import time 
start = time.time()

# Iterating through DataFrame using iterrows
for idx, row in df.iterrows():
# creating a new column 
df.at[idx,'ratio'] = 100 * (row["d"] / row["c"])
end = time.time()
print(end - start)
### 109 Seconds

Vektorisierung verwenden

start = time.time()
df["ratio"] = 100 * (df["d"] / df["c"])

end = time.time()
print(end - start)
### 0.12 seconds

Wir können eine deutliche Verbesserung im DataFrame erkennen, die Vektorisierung ist fast 1000-mal schneller im Vergleich zu Schleifen in Python.

Anwendungsfall 3: If-else-Anweisung auf DataFrame

Wir haben viele Operationen implementiert, die die Verwendung einer Logik vom Typ „if-else“ erfordern. Wir können diese Logik leicht durch vektorisierte Operationen in Python ersetzen.

Schauen Sie sich das Beispiel unten an, um es besser zu verstehen (wir werden den in Anwendungsfall 2 erstellten DataFrame verwenden).

Stellen Sie sich vor, wie Sie eine neue Spalte „e“ basierend auf einigen Bedingungen der verlassenen Spalte „a“ erstellen.

Schleifen verwenden

import time 
start = time.time()

# Iterating through DataFrame using iterrows
for idx, row in df.iterrows():
if row.a == 0:
df.at[idx,'e'] = row.d
elif (row.a <= 25) & (row.a > 0):
df.at[idx,'e'] = (row.b)-(row.c)
else:
df.at[idx,'e'] = row.b + row.c

end = time.time()

print(end - start)
### Time taken: 177 seconds

Vektorisierung verwenden

start = time.time()
df['e'] = df['b'] + df['c']
df.loc[df['a'] <= 25, 'e'] = df['b'] -df['c']
df.loc[df['a']==0, 'e'] = df['d']end = time.time()
print(end - start)
## 0.28007707595825195 sec

Im Vergleich zu Python-Schleifen mit if-else-Anweisungen sind vektorisierte Operationen 600-mal schneller als Schleifen.

Anwendungsfall 4: Maschinelles Lernen/Deep-Learning-Netzwerke lösen

Deep Learning erfordert, dass wir mehrere komplexe Gleichungen lösen, und das für Millionen und Abermilliarden von Gleichungsreihen. Das Ausführen von Schleifen in Python zur Lösung dieser Gleichungen ist sehr langsam, weshalb die Vektorisierung die beste Lösung ist.

Zum Beispiel möchten Sie die y-Werte für Millionen von Zeilen in der folgenden multilinearen Regressionsgleichung berechnen.

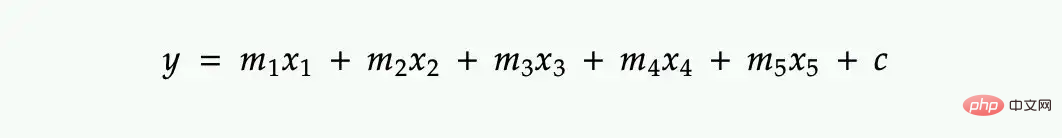
Wir können Schleifen durch Vektorisierung ersetzen. Die Werte von

m1,m2,m3... werden durch Lösen der obigen Gleichung unter Verwendung von Millionen von Werten bestimmt, die x1,x2,x3... entsprechen (sehen Sie sich zur Vereinfachung einfach einen einfachen Multiplikationsschritt an).

Erstellen Sie Daten

>>> import numpy as np
>>> # 设置 m 的初始值 
>>> m = np.random.rand(1,5)
array([[0.49976103, 0.33991827, 0.60596021, 0.78518515, 0.5540753]])
>>> # 500万行的输入值
>>> x = np.random.rand(5000000,5)

mithilfe von Schleifen

import numpy as np
m = np.random.rand(1,5)
x = np.random.rand(5000000,5)

total = 0
tic = time.process_time()

for i in range(0,5000000):
total = 0
for j in range(0,5):
total = total + x[i][j]*m[0][j] 

zer[i] = total 

toc = time.process_time()
print ("Computation time = " + str((toc - tic)) + "seconds")

####Computation time = 28.228 seconds

mithilfe der Vektorisierung

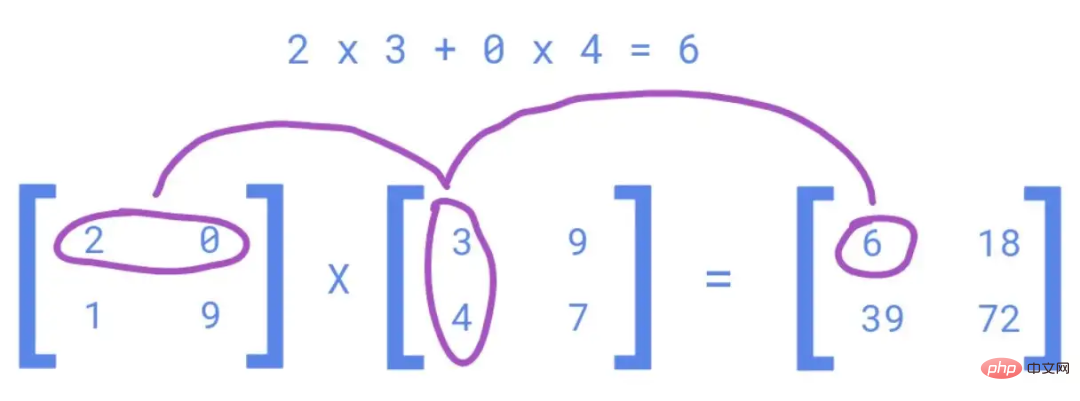
tic = time.process_time()

#dot product 
np.dot(x,m.T) 

toc = time.process_time()
print ("Computation time = " + str((toc - tic)) + "seconds")

####Computation time = 0.107 seconds

np.dot implementiert die Matrixmultiplikation von Vektoren im Ende. Im Vergleich zu Schleifen in Python ist es 165-mal schneller.

Am Ende geschrieben

Die Vektorisierung in Python ist sehr schnell, und wenn Sie mit sehr großen Datensätzen arbeiten, wird empfohlen, der Vektorisierung Vorrang vor Schleifen zu geben. Auf diese Weise werden Sie sich mit der Zeit allmählich daran gewöhnen, Code gemäß den Ideen der Vektorisierung zu schreiben.

Das obige ist der detaillierte Inhalt vonVerabschiedung! Python-Schleifen, Vektorisierung ist erstaunlich. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!