Heim >Backend-Entwicklung >Python-Tutorial >Python implementiert 12 Algorithmen zur Dimensionsreduktion
Python implementiert 12 Algorithmen zur Dimensionsreduktion
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-04-12 22:55:131876Durchsuche
Hallo zusammen, ich bin Peter~
Die Informationen zu verschiedenen Dimensionsreduktionsalgorithmen im Internet sind uneinheitlich und die meisten von ihnen stellen keinen Quellcode bereit. Hier ist ein GitHub-Projekt, das Python verwendet, um 11 klassische Datenextraktionsalgorithmen (Datendimensionalitätsreduzierung) zu implementieren, darunter: PCA, LDA, MDS, LLE, TSNE usw., mit relevanten Informationen und Anzeigeeffekten, die sich sehr gut für Anfänger und maschinelles Lernen eignen diejenigen, die gerade mit dem Data Mining begonnen haben.
Warum müssen wir eine Datendimensionalitätsreduktion durchführen?
Die sogenannte Dimensionsreduktion besteht darin, einen Satz von Vektoren Zi mit einer Anzahl von d zu verwenden, um die Vektoren Xi darzustellen mit einer Reihe von D. Nützliche Informationen, darunter d
Normalerweise werden wir feststellen, dass die Dimensionen der meisten Datensätze Hunderte oder sogar Tausende betragen und die Dimensionen des klassischen MNIST 64 betragen .

MNIST Handschriftlicher Zifferndatensatz
Aber in tatsächlichen Anwendungen benötigen die nützlichen Informationen, die wir verwenden, nicht so viele hohe Dimensionen , und die Anzahl der erforderlichen Proben nimmt mit jeder zusätzlichen Dimension exponentiell zu, was direkt zu einer großen „Dimensionalitätskatastrophe“ führen kann. Durch die Reduzierung der Datendimensionalität kann Folgendes erreicht werden:
#🎜🎜 #- Erleichterung des Datensatzes zu verwenden
- Sicherstellen, dass Variablen voneinander unabhängig sind
- Reduzieren Sie die Kosten für Algorithmusberechnungen
- Lineare Dimensionsreduktionsmethode: PCA, ICA LDA, LFA, LPP (lineare Darstellung von LE)
- Nichtlineare Dimensionsreduktionsmethode:
- # 🎜 🎜# Nichtlineare Dimensionsreduktionsmethode basierend auf Kernelfunktionen – KPCA, KICA, KDA
Nichtlineare Dimensionsreduktionsmethode (Flussmusterlernen) basierend auf Eigenwerten – ISOMAP, LLE, LE, LPP, LTSA , MVU
Heucoder, ein Masterstudent mit Schwerpunkt Computertechnologie am Harbin Institute of Technology, hat PCA, KPCA, LDA, MDS, ISOMAP, LLE, TSNE, AutoEncoder, FastICA, SVD zusammengestellt. Es gibt insgesamt Es werden zwölf klassische Dimensionsreduktionsalgorithmen in LE und LPP sowie relevante Informationen, Codes und Anzeigen bereitgestellt. Im Folgenden wird hauptsächlich der PCA-Algorithmus als Beispiel verwendet, um die spezifischen Operationen des Dimensionsreduktionsalgorithmus vorzustellen.
Dimensionalitätsreduktionsalgorithmus der Hauptkomponentenanalyse (PCA)
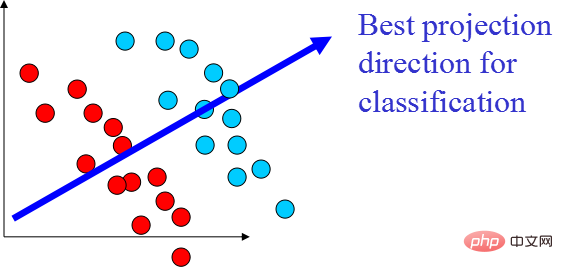
PCA ist eine Zuordnungsmethode, die auf der Zuordnung vom hochdimensionalen Raum zum niedrigdimensionalen Raum basiert und auch die grundlegendste ist Unüberwachte Reduktionsmethode Das Ziel des Dimensionsalgorithmus besteht darin, in die Richtung zu projizieren, in der sich die Daten am stärksten ändern, oder in die Richtung, in der der Rekonstruktionsfehler minimiert wird. Es wurde 1901 von Karl Pearson vorgeschlagen und ist eine lineare Dimensionsreduktionsmethode. Die mit PCA verbundenen Prinzipien werden oft als Theorie der maximalen Varianz oder Theorie des minimalen Fehlers bezeichnet. Beide haben das gleiche Ziel, aber der Prozessfokus ist unterschiedlich.
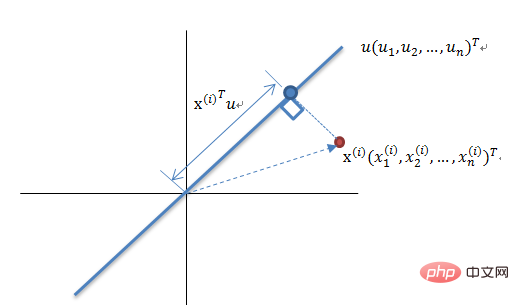 Dimensionalitätsreduktionsprinzip der Theorie der maximalen Varianz
Dimensionalitätsreduktionsprinzip der Theorie der maximalen Varianz
Reduzieren eines Satzes N-dimensionaler Vektoren auf K-dimensional (K ist größer als 0, kleiner als N), besteht das Ziel darin, K orthogonale Einheitenbasen auszuwählen, der COV(X,Y) jedes Feldes ist 0 und die Varianz des Feldes ist so groß wie möglich. Daher bedeutet die maximale Varianz, dass die Varianz der Projektionsdaten maximiert wird. In diesem Prozess müssen wir den besten Projektionsraum Wnxk, die beste Kovarianzmatrix usw. des Datensatzes Xmxn finden. Der Algorithmusablauf ist:
. #🎜🎜 #Algorithmuseingabe: Datensatz Xmxn;
- Berechnen Sie den Mittelwert Eigenwerte und entsprechende Eigenvektoren der Kovarianzmatrix COV;
- Platzieren Sie die Eigenwerte von groß nach klein. Sortieren Sie, wählen Sie die größten k aus und verwenden Sie dann die entsprechenden k Eigenvektoren als Spaltenvektoren, um die zu bilden Eigenvektormatrix Wnxk;
- Berechnen Sie XnewW, dh projizieren Sie den Datensatz Xnew auf die ausgewählten Eigenvektoren und erhalten Sie so den dimensionsreduzierten Datensatz XnewW, den wir benötigen.
- Minimum-Fehler-Theorie-Dimensionalitätsreduktionsprinzip
-
Der minimale Fehler ist die lineare Projektion, die die durchschnittlichen Projektionskosten minimiert. In diesem Prozess müssen wir Parameter wie die quadratische Fehlerbewertungsfunktion J0(x0) finden.
- PCA-Codeimplementierung (Principal Component Analysis)

Der Code für den PCA-Algorithmus lautet wie folgt:
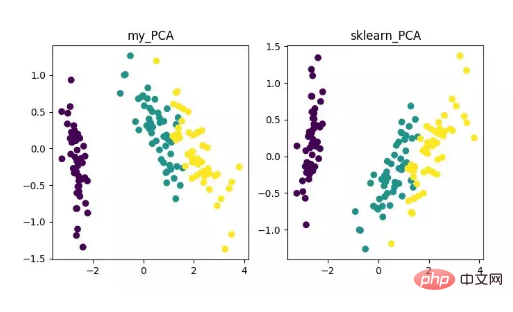
from __future__ import print_function from sklearn import datasets import matplotlib.pyplot as plt import matplotlib.cm as cmx import matplotlib.colors as colors import numpy as np %matplotlib inline def shuffle_data(X, y, seed=None): if seed: np.random.seed(seed) idx = np.arange(X.shape[0]) np.random.shuffle(idx) return X[idx], y[idx] # 正规化数据集 X def normalize(X, axis=-1, p=2): lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis)) lp_norm[lp_norm == 0] = 1 return X / np.expand_dims(lp_norm, axis) # 标准化数据集 X def standardize(X): X_std = np.zeros(X.shape) mean = X.mean(axis=0) std = X.std(axis=0) # 做除法运算时请永远记住分母不能等于 0 的情形 # X_std = (X - X.mean(axis=0)) / X.std(axis=0) for col in range(np.shape(X)[1]): if std[col]: X_std[:, col] = (X_std[:, col] - mean[col]) / std[col] return X_std # 划分数据集为训练集和测试集 def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None): if shuffle: X, y = shuffle_data(X, y, seed) n_train_samples = int(X.shape[0] * (1-test_size)) x_train, x_test = X[:n_train_samples], X[n_train_samples:] y_train, y_test = y[:n_train_samples], y[n_train_samples:] return x_train, x_test, y_train, y_test # 计算矩阵 X 的协方差矩阵 def calculate_covariance_matrix(X, Y=np.empty((0,0))): if not Y.any(): Y = X n_samples = np.shape(X)[0] covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0)) return np.array(covariance_matrix, dtype=float) # 计算数据集 X 每列的方差 def calculate_variance(X): n_samples = np.shape(X)[0] variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0))) return variance # 计算数据集 X 每列的标准差 def calculate_std_dev(X): std_dev = np.sqrt(calculate_variance(X)) return std_dev # 计算相关系数矩阵 def calculate_correlation_matrix(X, Y=np.empty([0])): # 先计算协方差矩阵 covariance_matrix = calculate_covariance_matrix(X, Y) # 计算 X, Y 的标准差 std_dev_X = np.expand_dims(calculate_std_dev(X), 1) std_dev_y = np.expand_dims(calculate_std_dev(Y), 1) correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T)) return np.array(correlation_matrix, dtype=float) class PCA(): """ 主成份分析算法 PCA,非监督学习算法. """ def __init__(self): self.eigen_values = None self.eigen_vectors = None self.k = 2 def transform(self, X): """ 将原始数据集 X 通过 PCA 进行降维 """ covariance = calculate_covariance_matrix(X) # 求解特征值和特征向量 self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance) # 将特征值从大到小进行排序,注意特征向量是按列排的,即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 个特征值对应的特征向量 idx = self.eigen_values.argsort()[::-1] eigenvalues = self.eigen_values[idx][:self.k] eigenvectors = self.eigen_vectors[:, idx][:, :self.k] # 将原始数据集 X 映射到低维空间 X_transformed = X.dot(eigenvectors) return X_transformed def main(): # Load the dataset data = datasets.load_iris() X = data.data y = data.target # 将数据集 X 映射到低维空间 X_trans = PCA().transform(X) x1 = X_trans[:, 0] x2 = X_trans[:, 1] cmap = plt.get_cmap('viridis') colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))] class_distr = [] # Plot the different class distributions for i, l in enumerate(np.unique(y)): _x1 = x1[y == l] _x2 = x2[y == l] _y = y[y == l] class_distr.append(plt.scatter(_x1, _x2, color=colors[i])) # Add a legend plt.legend(class_distr, y, loc=1) # Axis labels plt.xlabel('Principal Component 1') plt.ylabel('Principal Component 2') plt.show() if __name__ == "__main__": main()Schließlich erhalten wir die Ergebnisse der Dimensionsreduzierung wie folgt. Wenn Sie beispielsweise feststellen, dass die Anzahl der Merkmale (D) viel größer als die Anzahl der Stichproben (N) ist, können Sie einen kleinen Trick verwenden, um die Komplexitätsumwandlung des PCA-Algorithmus zu implementieren.

Anzeige des PCA-Dimensionalitätsreduktionsalgorithmus
Obwohl dieser Algorithmus klassisch und häufig verwendet wird, sind seine Mängel natürlich auch sehr offensichtlich. Es kann die lineare Korrelation sehr gut entfernen, aber bei Korrelationen höherer Ordnung ist der Effekt gering. Gleichzeitig besteht die Prämisse der PCA-Implementierung darin, davon auszugehen, dass die Hauptmerkmale der Daten in orthogonaler Richtung verteilt sind Für nicht orthogonale Richtungen gibt es mehrere Richtungen mit großen Abweichungen, und der Effekt von PCA wird stark reduziert.
Andere Dimensionsreduktionsalgorithmen und Codeadressen
- KPCA (Kernel-PCA)
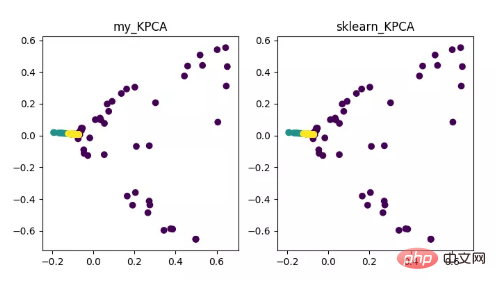
KPCA ist das Produkt der Kombination von Kernel-Technologie und PCA. Der Hauptunterschied zu PCA besteht darin, dass die Kernelfunktion bei der Berechnung der Kovarianzmatrix verwendet wird Das heißt, nach dem Kernel Die Kovarianzmatrix nach der Funktionszuordnung.
Die Einführung der Kernelfunktion kann das Problem der nichtlinearen Datenzuordnung sehr gut lösen. kPCA kann nichtlineare Daten einem hochdimensionalen Raum zuordnen, wobei Standard-PCA verwendet wird, um sie einem anderen niedrigdimensionalen Raum zuzuordnen.

Anzeige des KPCA-Dimensionalitätsreduktionsalgorithmus
Codeadresse:
https://github.com/heucoder/dimensionality_reduction_alo_codes/blob/master/codes/PCA/KPCA.py
- LDA (Lineare Diskriminanzanalyse)
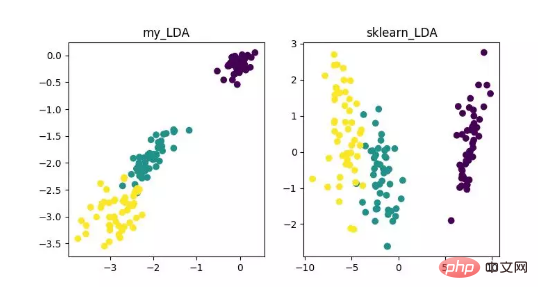
LDA ist eine Technologie, die zur Merkmalsextraktion verwendet werden kann. Ihr Ziel ist es, den Unterschied zwischen Klassen zu maximieren und den Unterschied innerhalb der Klasse zu minimieren, um Aufgaben wie die Klassifizierung effektiv zu erleichtern separate Proben verschiedener Klassen. LDA kann die Recheneffizienz im Datenanalyseprozess verbessern und die durch die Dimensionalitätskatastrophe verursachte Überanpassung bei Modellen, die nicht reguliert werden können, reduzieren.

Anzeige des LDA-Dimensionalitätsreduktionsalgorithmus
Codeadresse:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LDA
- MDS (mehrdimensionale Skalierung)
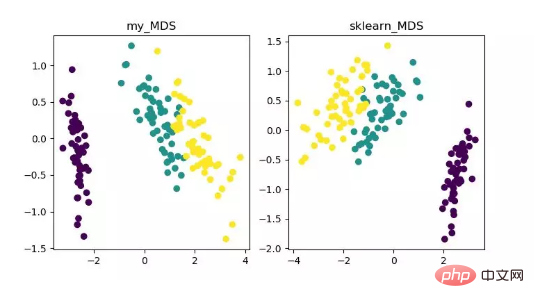
MDS ist mehrdimensional Die Skalierungsanalyse ist eine traditionelle Methode zur Dimensionsreduktion, die die Wahrnehmung und Präferenzen von Forschungsobjekten durch intuitive räumliche Karten darstellt. Diese Methode berechnet den Abstand zwischen zwei beliebigen Abtastpunkten, sodass der relative Abstand nach der Projektion in einen niedrigdimensionalen Raum beibehalten werden kann, um eine Projektion zu erreichen.
Da MDS in sklearn eine iterative Optimierungsmethode verwendet, werden im Folgenden sowohl iterative als auch nicht iterative Methoden implementiert. Anzeige des Algorithmus zur Reduzierung der MDS-Dimensionalität Dieser Algorithmus kann die Mängel des MDS-Algorithmus bei nichtlinear strukturierten Datensätzen gut beheben.
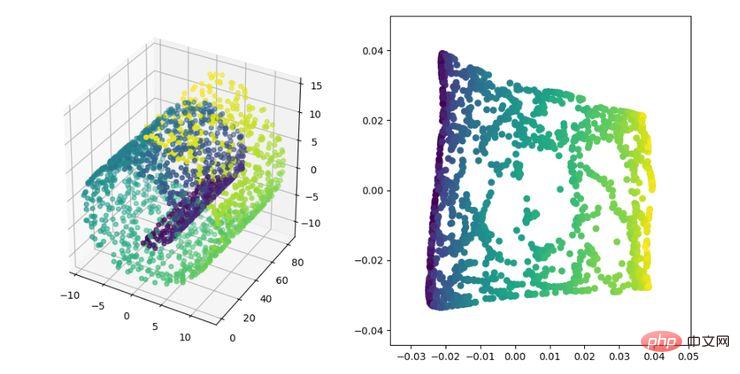
Der MDS-Algorithmus behält den Abstand zwischen den Proben nach der Dimensionsreduzierung bei, während der Isomap-Algorithmus ein Nachbarschaftsdiagramm einführt, das nur die Entfernung zwischen benachbarten Punkten berechnet und dann den Abstand zwischen ihnen aufrechterhält Distanz. Anzeige des Algorithmus zur Reduzierung der ISOMAP-Dimensionalität , ein nichtlinearer Dimensionsreduktionsalgorithmus. Die Kernidee dieses Algorithmus besteht darin, dass jeder Punkt durch eine lineare Kombination mehrerer benachbarter Punkte näherungsweise rekonstruiert werden kann und dann die hochdimensionalen Daten in einen niedrigdimensionalen Raum projiziert werden, sodass die lokale lineare Rekonstruktion zwischen ihnen beibehalten wird Datenpunkte haben eine Beziehung, das heißt, sie haben den gleichen Rekonstruktionskoeffizienten. Bei der sogenannten Mannigfaltigkeitsreduzierung ist der Effekt viel besser als bei PCA.

Anzeige des LLE-Dimensionalitätsreduktionsalgorithmus
Codeadresse:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LLE
- t-SNE
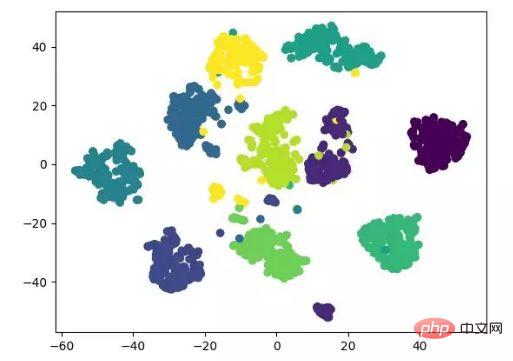
t-SNE ist auch eine Art Nicht -lineare Reduktion Der Dimensionsalgorithmus eignet sich sehr gut zum Reduzieren hochdimensionaler Daten auf zwei oder drei Dimensionen zur Visualisierung. Es handelt sich um einen unbeaufsichtigten Algorithmus für maschinelles Lernen, der den Datentrend in niedrigen Breitengraden (zwei oder drei Dimensionen) basierend auf dem ursprünglichen Trend der Daten rekonstruiert.
Die folgende Ergebnisanzeige bezieht sich auf den Quellcode und kann auch mit Tensorflow implementiert werden (keine manuelle Aktualisierung der Parameter erforderlich).

t-SNE-Dimensionalitätsreduktionsalgorithmus-Anzeige
Codeadresse:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/T-SNE
- LE(Laplace-Eigenkarten)
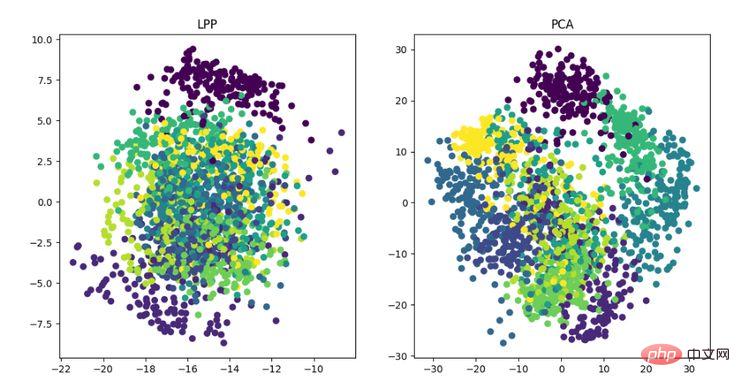
LE ist die Laplace-Feature-Map, die dem LLE-Algorithmus etwas ähnelt. Sie konstruiert auch die Beziehung zwischen Daten aus einer lokalen Perspektive. Seine intuitive Idee besteht darin, zu hoffen, dass Punkte, die miteinander in Beziehung stehen (im Diagramm verbundene Punkte), im dimensionsreduzierten Raum so nah wie möglich sind, um eine Lösung zu erhalten, die die geometrische Struktur der Mannigfaltigkeit widerspiegeln kann . Anzeige des LE-Algorithmus zur Dimensionsreduktion Die Idee des lokal erhaltenden Projektionsalgorithmus ähnelt der Laplace-Eigenkarte. Die Kernidee besteht darin, eine Projektionsabbildung zu erstellen, indem die Nachbarstrukturinformationen eines Datensatzes bestmöglich erhalten bleiben. LPP unterscheidet sich jedoch von LE darin, die Projektion direkt zu erhalten Ergebnis, das die Lösung der Projektionsmatrix erfordert.

Anzeige des LPP-Dimensionalitätsreduktionsalgorithmus
Codeadresse:
https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/LPP
- *Über den Autor des Projekts „dimensionality_reduction_alo_codes“
Heu Coder ist derzeit Masterstudent in Computertechnologie am Harbin Institute of Technology. Er trägt den Spitznamen „Super Love Learning“ auf Zhihu .com/heucoder.
Github-Projektadresse:
https://github.com/heucoder/dimensionality_reduction_alo_codes
Das obige ist der detaillierte Inhalt vonPython implementiert 12 Algorithmen zur Dimensionsreduktion. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!