Verwenden Sie Python, um die automatische Verfolgung von Raketen zu implementieren, super brennend!

Hallo zusammen, ich bin Bruder J.

Das ist ohne mathematische Grundlage schwer zu berechnen. Aber wenn wir Computer haben, ist das anders. Wenn wir uns auf die extrem hohe Rechengeschwindigkeit von Computern verlassen, können wir dies erreichen, indem wir die Idee der Differenzierung nutzen und ein wenig einfache Kenntnisse der Trigonometrie hinzufügen.

Okay, werfen wir ohne weiteres einen Blick auf das Algorithmusprinzip:

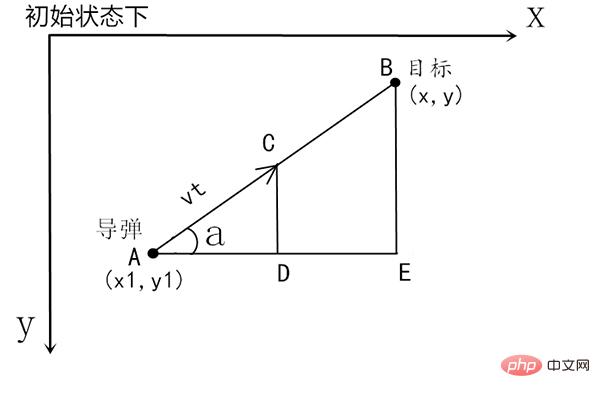
Da wir später Pygame verwenden werden, ist sein Koordinatensystem die y-Achse nach unten, also verwenden wir auch y hier. Abwärtskoordinatensystem.

Die allgemeine Idee des Algorithmus besteht darin, die Zeit t auf der Grundlage der obigen Abbildung in ausreichend kleine Segmente zu unterteilen (z. B. 1/1000, je kleiner die Zeitscheibe ist, desto genauer ist sie). Wie oben, um die Laufrichtung der Rakete (d. h. ∠a) und die zurückgelegte Distanz (d. h. vt=|AC|) zu berechnen. Zu diesem Zeitpunkt bewegt sich das Ziel erneut in der zweiten Zeitscheibe und dann Der gerade berechnete Punkt C wird zum zweiten Mal. Zu diesem Zeitpunkt wird in der zweiten Zeitscheibe ein Dreieck am Punkt C und dem neuen Zielpunkt konstruiert, um ein neues vt zu berechnen, und tritt dann in die dritte Zeitscheibe ein und so weiter.

Angenommen, die Anfangskoordinaten der Rakete und des Ziels sind (x1, y1), (x, y) und konstruieren ein rechtwinkliges Dreieck ABE. Dieses Dreieck wird verwendet, um die Sinus- und Kosinuswerte von ∠ zu ermitteln a, da vt von Ihnen selbst festgelegt wird, müssen wir berechnen, um wie viel sich die x- und y-Koordinaten von Punkt A verschoben haben. Der Wert der Bewegung ist die Länge von AD und CD. Diese beiden können mit vt cos(a) multipliziert werden ) bzw. sin(a).

Berechnen Sie sin(a) und cos(a), Sinus über Steigung, Cosinus neben Steigung, und die Hypotenuse kann mit der Zweipunkt-Abstandsformel berechnet werden, das heißt:

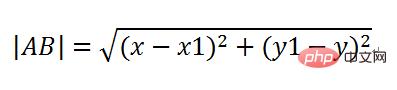
Also

Die Länge von AC beträgt: Die Geschwindigkeit der Rakete wird mit der Zeit multipliziert, was |AC|=vt ist, und dann können die Längen von AD und CD berechnet werden. Nachdem diese Zeitscheibe verstrichen ist, sollte die Rakete an der neuen Position erscheinen C, und seine Koordinaten sind der alte Punkt A. x erhöht AD und y minus CD.

Die neuen Koordinaten von Punkt C sind also:

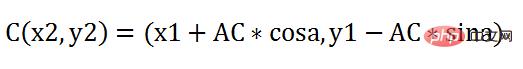
Wiederholen Sie diesen Vorgang einfach immer wieder. Um es anschaulicher zu machen, fügen wir den ersten Zeitabschnitt und den zweiten Zeitabschnitt zusammen:

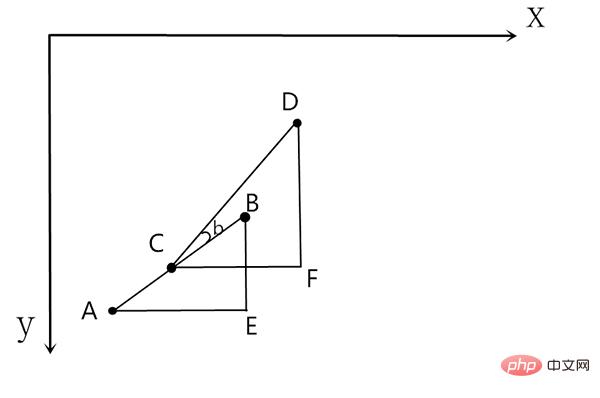
Das erste durch die Zeitscheibe konstruierte Dreieck ist ABE. Nach einer Zeitscheibe wandert das Ziel von Punkt B zu Punkt D. Die Rakete befindet sich zu diesem Zeitpunkt an Punkt C, daher wird ein neues Dreieck-CDF erstellt und der Berechnungsprozess wiederholt von Okay

Okay, da ich in letzter Zeit die Pygame-Bibliothek von Python verwendet habe, um kleine Spiele zu erstellen, werden wir Pygame verwenden, um diesen Effekt zu demonstrieren:

Der sehr einfache Code lautet wie folgt:

rrree

Wenn die Rakete nur als Partikel betrachtet wird, reicht der obige Algorithmus nicht aus, da ein Partikel nicht gedreht werden muss, unabhängig davon, ob es sich um einen Kopf oder einen Schwanz handelt dass sich das von Ihnen geladene Raketenbild nicht dreht, wenn es sehr klein ist. Es scheint kein Problem zu geben. Aber das Drehen in Pygame ist keine leichte Aufgabe. Lassen Sie uns zunächst das Bild durch ein Rechteck ersetzen und dann die Rotationsfunktion hinzufügen, um den Effekt zu sehen. Denn der Koordinatenpunkt des Bildes ist der obere linke Eckpunkt Wenn wir möchten, dass die Koordinaten des Bildes an der Spitze des Pfeils fixiert werden, reduzieren Sie einfach die tatsächliche Druckposition x des Bildes, indem Sie die Länge des Bildes reduzieren, und y, indem Sie die Breite um die Hälfte reduzieren. Aber der tatsächliche Betriebseffekt ist nicht gut:

大致方向相同，但是图片箭头的尖点并没有一直跟随鼠标，这是为什么呢。经过一番研究，我发现原来是这个图旋转的机制问题，我们看看旋转后的图片变成什么样了：

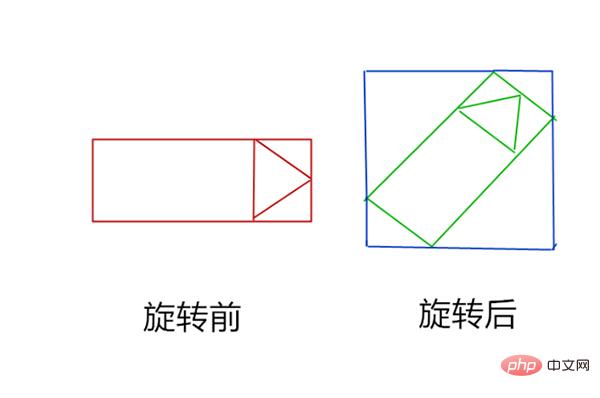
旋转后的图片变成了蓝色的那个范围，根据旋转角度的不同，所变成的图片大小也不一样，我们看旋转90的情况

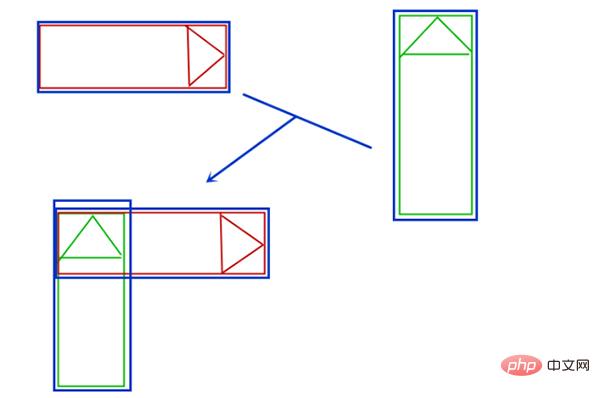
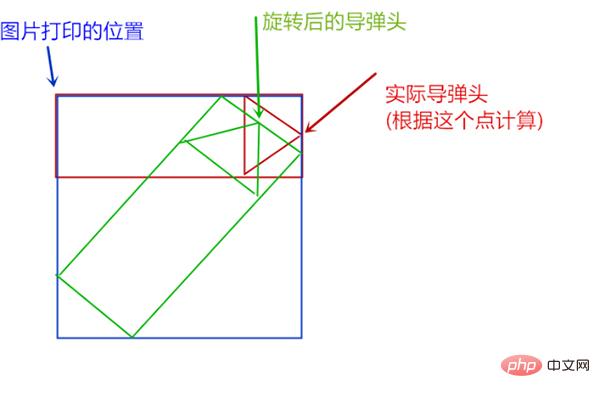
我们发现，旋转后的图片不仅面积变大了，导弹头的位置也变了。那应该怎么解决这个问题呢？思路是，每一次旋转图片以后，求出旋转图的头位置（图中的绿色箭头点），然后把绿图的打印位置移动一下，下，x，y分别移动两个头的距离，就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置，移动后应该是这样的：

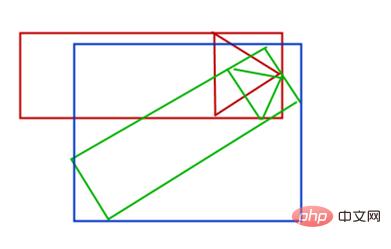
这样，两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同，旋转角在不同象限参数不一样，所以我们分为这四种情况

1，2象限

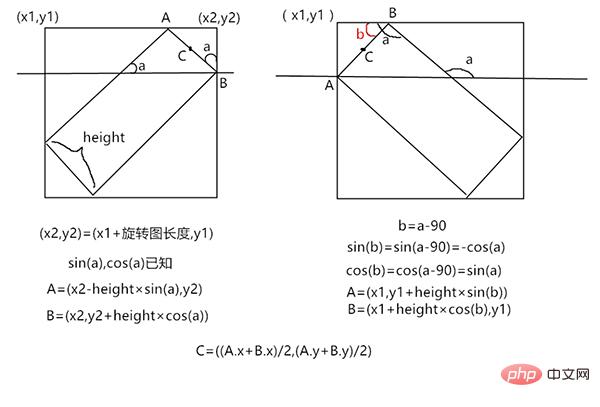
3，4象限，它的旋转只有正负0—180，所以3，4象限就是负角

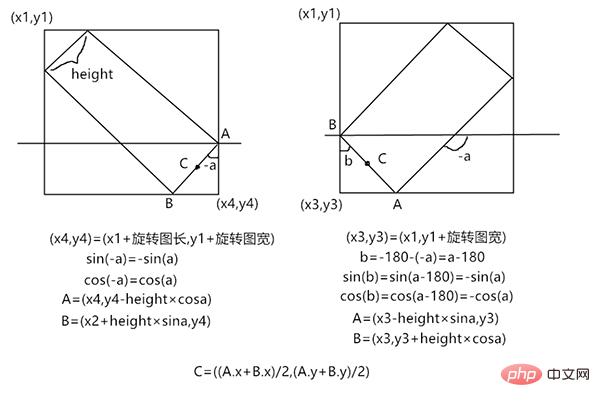
显示图片的时候我们将他移动

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)  

所以最后我们加入相关算法代码，效果就比较完美了

大功告成，最后附上全部的算法代码

import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()

以上便是用Python模拟导弹自动追踪的代码实例。

Das obige ist der detaillierte Inhalt vonVerwenden Sie Python, um die automatische Verfolgung von Raketen zu implementieren, super brennend!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!