Detaillierte Erläuterung der Prinzipien und Implementierung des minimalen und maximalen Heaps von Java-Datenstrukturen

Dieser Artikel vermittelt Ihnen relevantes Wissen über Java In der Informatik ist die Implementierung von Heap eine spezielle Baumstruktur, die eine Baumstruktur auf einem Array aufbauen und die Eigenschaften des Heaps erfüllen kann Über den Heap in der Java-Datenstruktur können Interessierte mehr erfahren.

Empfohlene Studie: „Java-Video-Tutorial“

1. Einführung

Geschichte des Heaps

Die Datenstruktur des Heaps hat viele Formen, einschließlich: 2-3 Heap, B-Heap, Fibonacci-Binär Heap, und der am häufigsten verwendete binäre Heap in der Java-API ist der binäre Heap, der zur Implementierung von Prioritätswarteschlangen verwendet wird. Er wurde 1964 von JWJ Williams als Datenstruktur für den Heap-Sortieralgorithmus eingeführt. Darüber hinaus ist der Heap auch in mehreren effizienten Graphalgorithmen wie dem Dijkstra-Algorithmus sehr wichtig.

2. Heap-Datenstruktur

In der Informatik ist die Implementierung von Heap eine spezielle Datenstruktur, die auf einem Array basiert und die Eigenschaften des Heaps erfüllt ist ein übergeordneter Knoten von C, dann sollte der Schlüssel (oder Wert) von P kleiner oder gleich dem entsprechenden Wert von C sein.

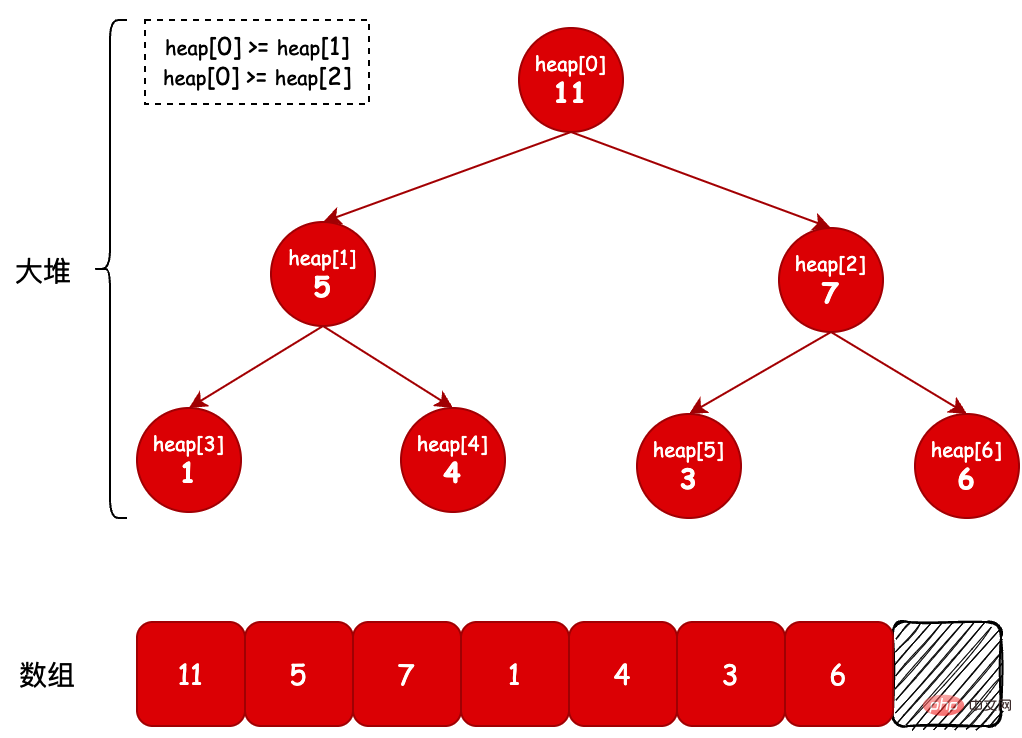
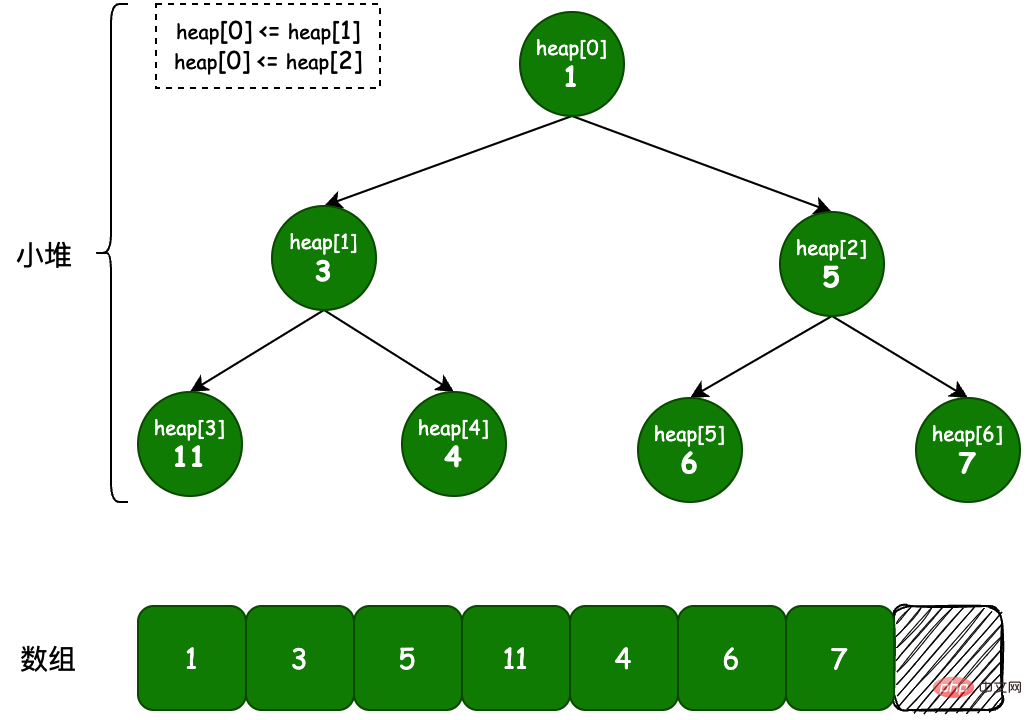Max Heap: Genau das Gegenteil der Definition von Min Heap. Im Max Heap (Max Heap) ist der Schlüssel (oder Wert) von P größer als der entsprechende Wert von C.

3. Heap-Code-Implementierung

1. Implementierungseinführung

Die Implementierung des Heaps in der Java-API spiegelt sich hauptsächlich in der Implementierung des Verzögerungswarteschlangen-Binär-Heaps wider Erfahren Sie separat mehr über die Implementierung von Small Heap und Large Heap.

Aus der Einführung in die Datenstruktur des Heaps können wir erkennen, dass der einzige Unterschied zwischen einem kleinen Heap und einem großen Heap in der Art der Sortierung der Elemente besteht. Das heißt, beim Speichern und Abrufen von Elementen sowie beim Füllen und Entfernen von Elementen ist die Sortiermethode unterschiedlich.

2. Heap-Implementierung

Beim Speichern von Elementen im Heap werden die Elemente am Ende der Warteschlange verglichen und während des Speichervorgangs nach oben migriert, um ihren Eigenschaften zu folgen.

private void siftUpComparable(int k, E x) {
    logger.info("【入队】元素：{} 当前队列：{}", JSON.toJSONString(x), JSON.toJSONString(queue));
    while (k > 0) {
        // 获取父节点Idx，相当于除以2
        int parent = (k - 1) >>> 1;
        logger.info("【入队】寻找当前节点的父节点位置。k：{} parent：{}", k, parent);
        Object e = queue[parent];
        // 如果当前位置元素，大于父节点元素，则退出循环
        if (compareTo(x, (E) e) >= 0) {
            logger.info("【入队】值比对，父节点：{} 目标节点：{}", JSON.toJSONString(e), JSON.toJSONString(x));
            break;
        }
        // 相反父节点位置大于当前位置元素，则进行替换
        logger.info("【入队】替换过程，父子节点位置替换，继续循环。父节点值：{} 存放到位置：{}", JSON.toJSONString(e), k);
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
    logger.info("【入队】完成 Idx：{} Val：{} \r\n当前队列：{} \r\n", k, JSON.toJSONString(x), JSON.toJSONString(queue));
}

Die Implementierung des Hinzufügens der Add-Methode zum Heap ruft schließlich die siftUpComparable-Methode zur sortierenden Verarbeitung auf. Diese Sortiermethode „compareTo“ wird durch bestimmte MinHeap- und MaxHeap-Methoden implementiert.

Nehmen Sie als Beispiel das Heap-Element 2, wie in der Abbildung gezeigt.

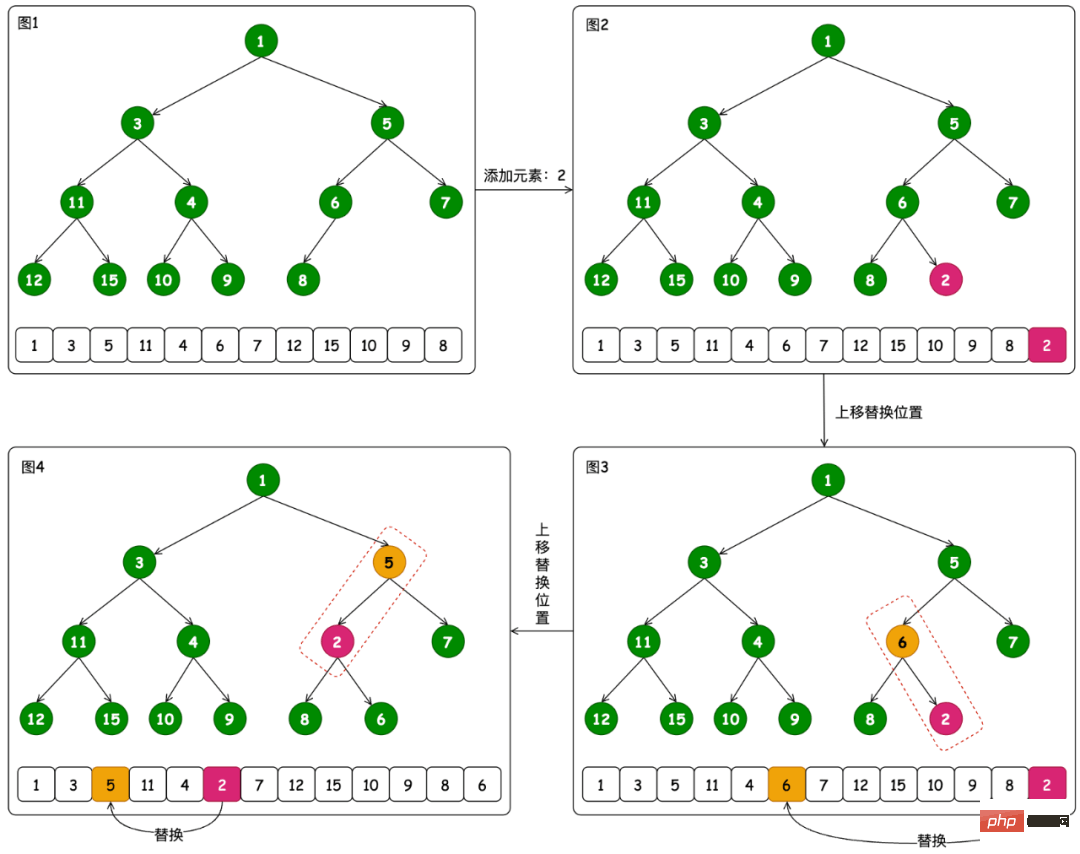Hängen Sie zuerst Element 2 an das Ende der Warteschlange, berechnen Sie dann die Position des übergeordneten Knotens durch (k - 1) >>>, vergleichen und beurteilen Sie den Austausch mit dem entsprechenden Element.

Der Austauschvorgang umfasst 2->6, 2->5, danach werden die Elemente gespeichert.

3. Das Verlassen von Elementen aus dem Heap ist eigentlich sehr einfach. Löschen Sie einfach das Stammelement und öffnen Sie es direkt. Die verbleibenden Schritte sind jedoch kompliziert, da nach der Migration des Stammelements ein weiteres Mindestelement für die Migration zum anderen Ende gefunden werden muss. Dieser Prozess ist genau das Gegenteil des Betretens des Heaps. Es handelt sich um einen Prozess der kontinuierlichen Abwärtsmigration.

private void siftDownComparable(int k, E x) {
    // 先找出中间件节点
    int half = size >>> 1;
    while (k < half) {
        // 找到左子节点和右子节点，两个节点进行比较，找出最大的值
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        // 左子节点与右子节点比较，取最小的节点
        if (right < size && compareTo((E) c, (E) queue[right]) > 0) {
            logger.info("【出队】左右子节点比对，获取最小值。left：{} right：{}", JSON.toJSONString(c), JSON.toJSONString(queue[right]));
            c = queue[child = right];
        }
        // 目标值与c比较，当目标值小于c值，退出循环。说明此时目标值所在位置适合，迁移完成。
        if (compareTo(x, (E) c) <= 0) {
            break;
        }
        // 目标值小于c值，位置替换，继续比较
        logger.info("【出队】替换过程，节点的值比对。上节点：{} 下节点：{} 位置替换", JSON.toJSONString(queue[k]), JSON.toJSONString(c));
        queue[k] = c;
        k = child;
    }
    // 把目标值放到对应位置
    logger.info("【出队】替换结果，最终更换位置。Idx：{} Val：{}", k, JSON.toJSONString(x));
    queue[k] = x;
}

Elemente kontinuierlich nach unten migrieren. Bei diesem Vorgang werden die Werte des linken und rechten untergeordneten Knotens verglichen und der kleinste ermittelt. Daher wird der gesamte Vorgang mühsamer sein als das Betreten des Stapels.

Hier nehmen wir Popup-Element 1 als Beispiel und ersetzen dann das Element am Ende des Heaps an der entsprechenden Position. Der gesamte Vorgang ist in 6 Bilder unterteilt.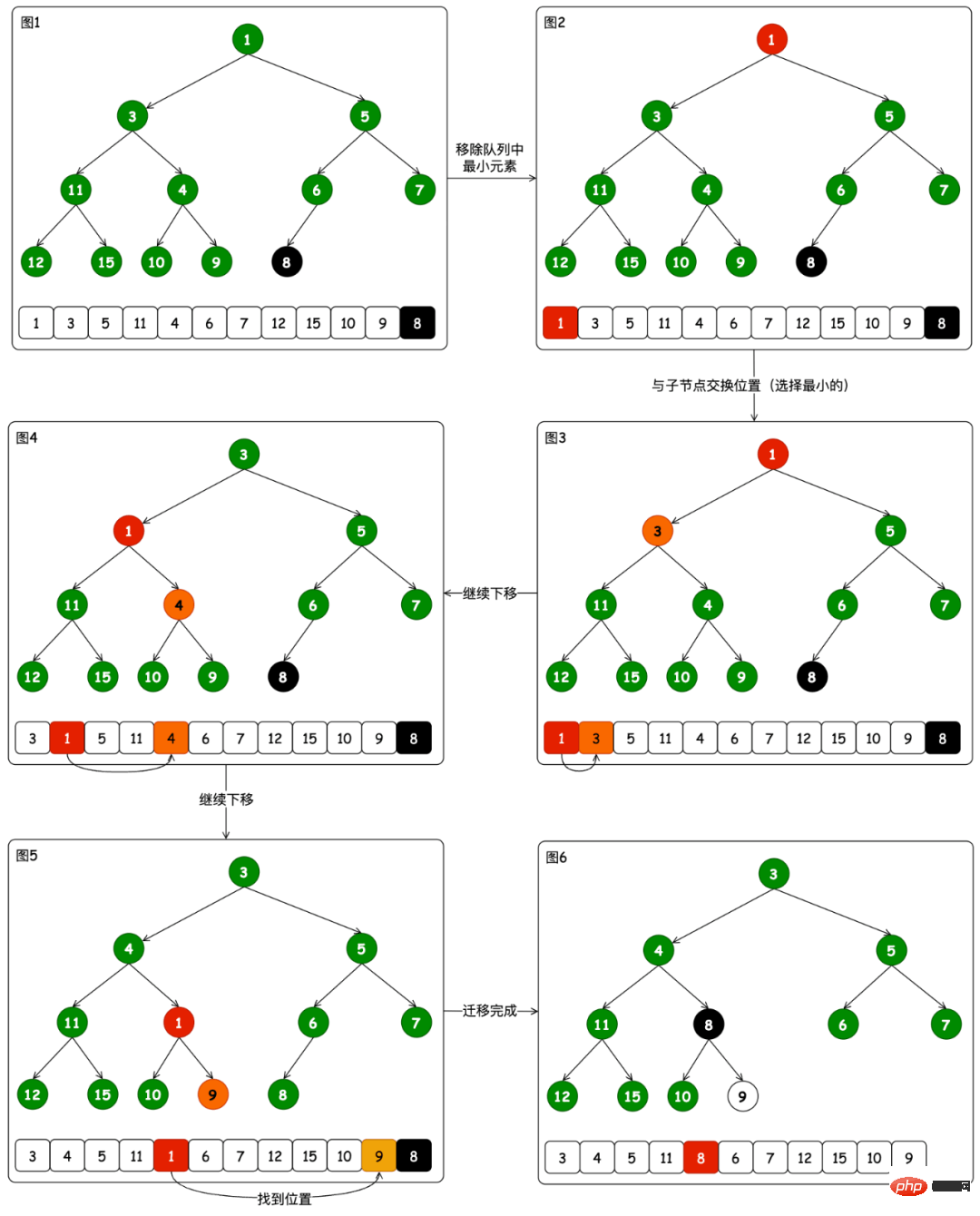

Abbildung 1 bis Abbildung 2: Suchen Sie das Stammelement, das angezeigt werden soll.

Von Abbildung 3 bis Abbildung 4: Verschieben Sie das Stammelement nach unten, vergleichen Sie es mit den untergeordneten Elementen und ersetzen Sie die Position. Wenn diese Position mit 8 verglichen wird und kleiner als 8 ist, wandert sie weiter nach unten.

• Von Abbildung 4 bis Abbildung 5 setzen Sie die Migration fort. Die beiden Unterelemente, die der Position des ursprünglichen Knotens 4 entsprechen, sind beide größer als 8. Sie können zu diesem Zeitpunkt anhalten.
• Abbildung 5 bis Abbildung 6: Ändern Sie die Elementposition und ersetzen Sie das Element am Ende der Warteschlange an der Position, die der Abwärtsmigrationserkennung von Element 1 entspricht.
• 4. Kleine Heap-Implementierung

Kleiner Heap ist ein positiver Sequenzvergleich

public class MinHeap extends Heap<Integer> {

    @Override
    public int compareTo(Integer firstElement, Integer secondElement) {
        return firstElement.compareTo(secondElement);
    }

}

Test

@Test
public void test_min_heap() {
    MinHeap heap = new MinHeap();
    // 存入元素
    heap.add(1);
    heap.add(3);
    heap.add(5);
    heap.add(11);
    heap.add(4);
    heap.add(6);
    heap.add(7);
    heap.add(12);
    heap.add(15);
    heap.add(10);
    heap.add(9);
    heap.add(8);
    // 弹出元素
    while (heap.peek() != null){
        logger.info("测试结果：{}", heap.poll());
    }
}

Ergebnis

17:21:30.053 [main] INFO queue.PriorityQueue – [Enqueue] Element: 3 Aktuelle Warteschlange: [1,null,null,null,null,null,null,null,null,null,null,null]
17: 21:30.055 [main] INFO queue.PriorityQueue – [Enqueue] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 1 übergeordneter Knoten: 0
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 1 Zielknoten: 3
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 1 Wert: 3
Aktuelle Warteschlange: [1,3,null,null,null,null,null,null,null,null,null]

17:21:30.056 [Haupt] INFO-Warteschlange .PriorityQueue – [Enqueue] Element: 5 Aktuelle Warteschlange: [1,3,null,null,null,null,null,null,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue – [ Geben Sie die Warteschlange ein] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 2 übergeordneter Knoten: 0
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 1 Zielknoten: 5
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 2 Wert: 5
Aktuelle Warteschlange: [1,3,5,null,null,null,null,null,null,null,null]

17:21:30.056 [Haupt] INFO-Warteschlange .PriorityQueue – [Warteschlange eingeben] Element: 11 Aktuelle Warteschlange: [1,3,5,null,null,null,null,null,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue – [Betreten Sie die Warteschlange] Suchen Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 3 übergeordneter Knoten: 1
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 3 Zielknoten: 11
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 3 Val: 11
Aktuelle Warteschlange: [1,3,5,11,null,null,null,null,null,null,null]

17:21:30.056 [Haupt] INFO-Warteschlange .PriorityQueue – [Enqueue] Element: 4 Aktuelle Warteschlange: [1,3,5,11,null,null,null,null,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue – [ Geben Sie die Warteschlange ein] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 4 übergeordneter Knoten: 1
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 3 Zielknoten: 4
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 4 Wert: 4
Aktuelle Warteschlange: [1,3,5,11,4,null,null,null,null,null,null]

17:21:30.056 [Haupt] INFO-Warteschlange .PriorityQueue – [Warteschlange eingeben] Elemente: 6 Aktuelle Warteschlange: [1,3,5,11,4,null,null,null,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue – [Betreten Sie die Warteschlange] Suchen Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 5 übergeordneter Knoten: 2
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 5 Zielknoten: 6
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 5 Val: 6
Aktuelle Warteschlange: [1,3,5,11,4,6,null,null,null,null,null]

17:21:30.056 [Haupt] INFO-Warteschlange .PriorityQueue – [Warteschlange eingeben] Element: 7 Aktuelle Warteschlange: [1,3,5,11,4,6,null,null,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue – [Betreten Sie die Warteschlange] Suchen Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 6 übergeordneter Knoten: 2
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 5 Zielknoten: 7
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 6 Val: 7
Aktuelle Warteschlange: [1,3,5,11,4,6,7,null,null,null,null] 17:21:30.056 [main] INFO queue.PriorityQueue - [Enter Queue] Element: 12 Aktuelle Warteschlange: [1,3,5,11,4,6,7,null,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue - [Enter Team] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 7 übergeordneter Knoten: 3
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 11 Zielknoten: 12
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 7 Val: 12
Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,null,null,null]

17:21:30.056 [Haupt] INFO-Warteschlange .PriorityQueue – [Enqueue] Element: 15 Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,null,null,null]
17:21:30.056 [main] INFO queue.PriorityQueue – [ Geben Sie die Warteschlange ein] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 8 übergeordneter Knoten: 3
17:21:30.056 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 11 Zielknoten: 15
17:21:30.057 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 8 Val: 15
Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,null,null]

17:21:30.057 [Haupt] INFO-Warteschlange .PriorityQueue – [Enqueue] Elemente: 10 Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,null,null]
17:21:30.057 [main] INFO queue.PriorityQueue – [ Geben Sie die Warteschlange ein] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 9 übergeordneter Knoten: 4
17:21:30.057 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 4 Zielknoten: 10
17:21:30.057 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 9 Val: 10
Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,10,null]

17:21:30.057 [Haupt] INFO-Warteschlange .PriorityQueue – [Enqueue] Element: 9 Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,10,null]
17:21:30.057 [main] INFO queue.PriorityQueue – [ Geben Sie die Warteschlange ein] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k:10 Elternteil:4
17:21:30.057 [main] INFO queue.PriorityQueue – [Enter Queue] Wertevergleich, übergeordneter Knoten: 4 Zielknoten: 9
17:21:30.057 [main] INFO queue.PriorityQueue – [Enter Queue] Abschluss-IDx: 10 Wert: 9
Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,10,9]

17:21:30.057 [Haupt] INFO queue.PriorityQueue – [Warteschlange betreten] Elemente: 8 Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,10,9,null,null,null,null,null,null,null,null,null,null,null ,null,null]
17:21:30.057 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 11 übergeordneter Knoten: 5
17:21:30.057 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 6 Zielknoten: 8
17:21:30.057 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 11 Val: 8
Aktuelle Warteschlange: [1,3,5,11,4,6,7,12,15,10,9,8,null,null,null,null,null, null,null,null,null,null,null,null]

17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 1 Unterer Knoten: 3 Positionsersetzung
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 11 rechts: 4
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue]-Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 3 Unterer Knoten: 4 Positionsersetzung
17:21:30.057 [main] INFO queue.PriorityQueue - [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 10 rechts: 9
17:21:30.057 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 4 Val: 8
17:21:30.057 [main] INFO heap.__test__.HeapTest – Testergebnis: 1
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 3 Unterer Knoten: 4 Positionsersetzung
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 11 rechts: 8
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 4 Unterer Knoten: 8 Positionsersetzung
17:21:30.057 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 4 Val: 9
17:21:30.057 [main] INFO heap.__test__.HeapTest – Testergebnis: 3
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Vergleich der linken und rechten untergeordneten Knoten , Holen Sie sich den Mindestwert. links: 8 rechts: 5
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue]-Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 4 Unterer Knoten: 5 Positionsersetzung
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 5 Unterer Knoten: 6 Positionsersetzung
17:21:30.057 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 5 Val: 10
17:21:30.057 [main] INFO heap.__test__.HeapTest – Testergebnis: 4
17:21:30.057 [main] INFO queue.PriorityQueue – [Dequeue] Vergleich der linken und rechten untergeordneten Knoten , Holen Sie sich den Mindestwert. links: 8 rechts: 6
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 5 Unterer Knoten: 6 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 10 rechts: 7
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue]-Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 6 Unterer Knoten: 7 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 6 Val: 15
17:21:30.058 [main] INFO heap.__test__.HeapTest – Testergebnis: 5
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Vergleich der linken und rechten untergeordneten Knoten , Holen Sie sich den Mindestwert. links: 8 rechts: 7
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue]-Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 6 Unterer Knoten: 7 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 7 Unterer Knoten: 10 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 5 Val: 12
17:21:30.058 [main] INFO heap.__test__.HeapTest – Testergebnis: 6
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 7 Unterer Knoten: 8 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 11 rechts: 9
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue]-Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 8 Unterer Knoten: 9 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 4 Val: 15
17:21:30.058 [main] INFO heap.__test__.HeapTest – Testergebnis: 7
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 8 Unterer Knoten: 9 Positionsersetzung
17:21:30.058 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 9 Unterer Knoten: 11 Positionsersatz
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：3 Val：12
17:21:30.058 [main] INFO heap.__test__.HeapTest - 测试结果：8
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】左右子节点比对，获取最小值。left：11 right：10
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：9 下节点：10 位置替换
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：2 Val：15
17:21:30.058 [main] INFO heap.__test__.HeapTest - 测试结果：9
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：10 下节点：11 位置替换
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：1 Val：12
17:21:30.058 [main] INFO heap.__test__.HeapTest - 测试结果：10
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换过程，节点的值比对。上节点：11 下节点：12 位置替换
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：1 Val：15
17:21:30.058 [main] INFO heap.__test__.HeapTest - 测试结果：11
17:21:30.058 [main] INFO queue.PriorityQueue - 【出队】替换结果，最终更换位置。Idx：0 Val：15
17:21:30.058 [main] INFO heap.__test__.HeapTest - 测试结果：12
17:21:30.058 [main] INFO heap.__test__.HeapTest - 测试结果：15

Process finished with exit code 0
小堆就是一个正序的输出结果，从小到大的排序和输出。
小堆空间：[1,3,5,11,4,6,7,12,15,10,9,8,null,null,null,null,null,null,null,null,null,null,null,null]

• 小堆就是一个正序的输出结果，从小到大的排序和输出。
• 小堆空间：[1,3,5,11,4,6,7,12,15,10,9,8,null,null,null,null,null,null,null,null,null,null,null,null]

5. 大堆实现

小堆是一个反序比对

public class MaxHeap extends Heap<Integer> {

    @Override
    public int compareTo(Integer firstElement, Integer secondElement) {
        return secondElement.compareTo(firstElement);
    }

}

测试

@Test
public void test_max_heap() {
    MaxHeap heap = new MaxHeap();
    // 存入元素
    heap.add(1);
    heap.add(3);
    heap.add(5);
    heap.add(11);
    heap.add(4);
    heap.add(6);
    heap.add(7);
    heap.add(12);
    heap.add(15);
    heap.add(10);
    heap.add(9);
    heap.add(8);
    // 弹出元素
    while (heap.peek() != null){
        logger.info("测试结果：{}", heap.poll());
    }
}

结果

17:23:45.079 [main] INFO queue.PriorityQueue – [Enqueue] Element: 3 Aktuelle Warteschlange: [1,null,null,null,null,null,null,null,null,null,null]
17: 23:45.081 [main] INFO queue.PriorityQueue – [Enqueue] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 1 parent: 0
17:23:45.081 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 1 Gespeichert an Position: 1
17:23:45.081 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Abgeschlossene Idx: 0 Wert: 3
Aktuelle Warteschlange: [3,1,null,null,null, null,null,null,null,null,null]

17:23:45.081 [main] INFO queue.PriorityQueue – [Enqueue] Element: 5 Aktuelle Warteschlange: [3,1,null,null,null,null, null ,null,null,null,null]
17:23:45.081 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 2 parent: 0
17:23:45.081 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 3 Gespeichert an Position: 2
17:23:45.081 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Abgeschlossene ID: 0 Wert: 5
Aktuelle Warteschlange: [5,1,3,null,null, null,null,null,null,null,null]

17:23:45.081 [main] INFO queue.PriorityQueue – [Enqueue] Element: 11 Aktuelle Warteschlange: [5,1,3,null,null,null, null ,null,null,null,null]
17:23:45.081 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 3 parent: 1
17:23:45.081 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 1 Gespeichert an Ort: 3
17:23:45.081 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 1 parent: 0
17:23:45.081 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 5 Gespeichert an Position: 1
17:23:45.081 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Abgeschlossene ID: 0 Wert: 11
Aktuelle Warteschlange: [11,5,3,1,null, null,null,null,null,null,null]

17:23:45.081 [main] INFO queue.PriorityQueue – [Enqueue] Element: 4 Aktuelle Warteschlange: [11,5,3,1,null,null, null ,null,null,null,null]
17:23:45.082 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 4 übergeordneter Knoten: 1
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 5 Zielknoten: 4
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 4 Wert: 4
Aktuelle Warteschlange: [11,5,3,1,4,null,null,null,null,null,null]

17:23:45.082 [Haupt] INFO-Warteschlange .PriorityQueue – [Warteschlange eingeben] Element: 6 Aktuelle Warteschlange: [11,5,3,1,4,null,null,null,null,null,null]
17:23:45.082 [main] INFO queue.PriorityQueue – [Betreten Sie die Warteschlange] Suchen Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 5 parent: 2
17:23:45.082 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 3 Gespeichert an Ort: 5
17:23:45.082 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 2 übergeordneter Knoten: 0
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 11 Zielknoten: 6
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 2 Val: 6
Aktuelle Warteschlange: [11,5,6,1,4,3,null,null,null,null,null]

17:23:45.082 [Haupt] INFO-Warteschlange .PriorityQueue – [Warteschlange eingeben] Element: 7 Aktuelle Warteschlange: [11,5,6,1,4,3,null,null,null,null,null]
17:23:45.082 [main] INFO queue.PriorityQueue – [Betreten Sie die Warteschlange] Suchen Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 6 parent: 2
17:23:45.082 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 6 Gespeichert an Position: 6
17:23:45.082 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 2 übergeordneter Knoten: 0
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 11 Zielknoten: 7
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 2 Wert: 7
Aktuelle Warteschlange: [11,5,7,1,4,3,6,null,null,null,null]

17:23:45.082 [Haupt] INFO-Warteschlange .PriorityQueue – [Warteschlange eingeben] Element: 12 Aktuelle Warteschlange: [11,5,7,1,4,3,6,null,null,null,null]
17:23:45.082 [main] INFO queue.PriorityQueue – [Betreten Sie die Warteschlange] Suchen Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 7 parent: 3
17:23:45.082 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 1 Gespeichert an Position: 7
17:23:45.082 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 3 parent: 1
17:23:45.082 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 5 Gespeichert an Ort: 3
17:23:45.082 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 1 Elternteil: 0
17:23:45.082 [main] INFO queue.PriorityQueue – [Enqueue] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 11 Gespeichert an Position: 1
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Abgeschlossene ID: 0 Wert: 12
Aktuelle Warteschlange: [12,11,7,5,4, 3,6,1,null,null,null]

17:23:45.082 [main] INFO queue.PriorityQueue – [Enqueue] Element: 15 Aktuelle Warteschlange: [12,11,7,5,4,3, 6 ,1,null,null,null]
17:23:45.082 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 8 parent: 3
17:23:45.082 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 5 Gespeichert an Ort: 8
17:23:45.082 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 3 parent: 1
17:23:45.082 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 11 Gespeichert an Position: 3
17:23:45.082 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 1 parent: 0
17:23:45.082 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 12 Gespeichert an Position: 1
17:23:45.082 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Abgeschlossene ID: 0 Wert: 15
Aktuelle Warteschlange: [15,12,7,11,4, 3,6,1,5,null,null]

17:23:45.082 [main] INFO queue.PriorityQueue – [Enqueue] Element: 10 Aktuelle Warteschlange: [15,12,7,11,4,3, 6 ,1,5,null,null]
17:23:45.082 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 9 parent: 4
17:23:45.083 [main] INFO queue.PriorityQueue - [Warteschlange betreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 4 Gespeichert an Ort: 9
17:23:45.083 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 4 übergeordneter Knoten: 1
17:23:45.083 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 12 Zielknoten: 10
17:23:45.083 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 4 Wert: 10
Aktuelle Warteschlange: [15,12,7,11,10,3,6,1,5,4,null]

17:23:45.083 [Haupt] INFO-Warteschlange .PriorityQueue – [Enqueue] Element: 9 Aktuelle Warteschlange: [15,12,7,11,10,3,6,1,5,4,null]
17:23:45.083 [main] INFO queue.PriorityQueue – [ Geben Sie die Warteschlange ein] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 10 übergeordneter Knoten: 4
17:23:45.083 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 10 Zielknoten: 9
17:23:45.083 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 10 Val: 9
Aktuelle Warteschlange: [15,12,7,11,10,3,6,1,5,4,9]

17:23:45.083 [Haupt-]INFO-Warteschlange .PriorityQueue – [Enqueue] Element: 8 Aktuelle Warteschlange: [15,12,7,11,10,3,6,1,5,4,9,null,null,null,null,null,null,null, null ,null,null,null,null,null]
17:23:45.083 [main] INFO queue.PriorityQueue – [Enqueue] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 11 parent: 5
17:23:45.083 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 3 Gespeichert an Ort: 11
17:23:45.083 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 5 parent: 2
17:23:45.083 [main] INFO queue.PriorityQueue - [In die Warteschlange eintreten] Ersetzungsprozess, die Position der übergeordneten und untergeordneten Knoten wird ersetzt und der Zyklus wird fortgesetzt. Wert des übergeordneten Knotens: 7 Gespeichert an Ort: 5
17:23:45.083 [Haupt] INFO queue.PriorityQueue - [Warteschlange betreten] Finden Sie die Position des übergeordneten Knotens des aktuellen Knotens. k: 2 übergeordneter Knoten: 0
17:23:45.083 [Haupt] INFO queue.PriorityQueue – [Warteschlange eingeben] Wertevergleich, übergeordneter Knoten: 15 Zielknoten: 8
17:23:45.083 [Haupt] INFO queue.PriorityQueue – [ Betreten Sie die Warteschlange] Abgeschlossene Idx: 2 Wert: 8
Aktuelle Warteschlange: [15,12,8,11,10,7,6,1,5,4,9,3,null,null,null,null,null, null,null,null,null,null,null,null]

17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 15 Unterer Knoten: 12 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 12 Unterer Knoten: 11 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 1 rechts: 5
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 11 Unterer Knoten: 5 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 8 Val: 3
17:23:45.083 [main] INFO heap.__test__.HeapTest – Testergebnis: 15
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 12 Unterer Knoten: 11 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 5 rechts: 10
17:23:45.083 [main] INFO queue.PriorityQueue – [Entfernen] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 11 Unterer Knoten: 10 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 4 Val: 9
17:23:45.083 [main] INFO heap.__test__.HeapTest – Testergebnis: 12
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 11 Unterer Knoten: 10 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Vergleichen Sie den linken und rechten untergeordneten Knoten, um den Mindestwert zu erhalten. links: 5 rechts: 9
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 10 Unterer Knoten: 9 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 4 Val: 4
17:23:45.083 [main] INFO heap.__test__.HeapTest – Testergebnis: 11
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 10 Unterer Knoten: 9 Positionsersetzung
17:23:45.083 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 9 Unterer Knoten: 5 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 3 Val: 3
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 10
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Vergleich der linken und rechten untergeordneten Knoten , Holen Sie sich den Mindestwert. links: 5 rechts: 8
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 9 Unterer Knoten: 8 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 8 Unterer Knoten: 7 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 5 Val: 1
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 9
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Vergleich der linken und rechten untergeordneten Knoten , Holen Sie sich den Mindestwert. links: 5 rechts: 7
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 8 Unterer Knoten: 7 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 2 Val: 6
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 8
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Vergleich der linken und rechten untergeordneten Knoten , Holen Sie sich den Mindestwert. links: 5 rechts: 6
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwertvergleich. Oberer Knoten: 7 Unterer Knoten: 6 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 2 Val: 1
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 7
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 6 Unterer Knoten: 5 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 1 Val: 4
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 6
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 5 Unterer Knoten: 4 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 1 Val: 3
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 5
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsprozess, Knotenwert vergleichen. Oberer Knoten: 4 Unterer Knoten: 3 Positionsersetzung
17:23:45.084 [main] INFO queue.PriorityQueue - [Dequeue] Ersetzen Sie das Ergebnis und ändern Sie schließlich die Position. Idx: 1 Val: 1
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 4
17:23:45.084 [main] INFO queue.PriorityQueue – [Dequeue] Ersetzungsergebnis, endgültige Ersetzungsposition. Idx: 0 Val: 1
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 3
17:23:45.084 [main] INFO heap.__test__.HeapTest – Testergebnis: 1

Prozess abgeschlossen mit Exit-Code 0

Der große Stapel ist das Ausgabeergebnis in umgekehrter Reihenfolge, sortiert und von groß nach klein ausgegeben.

Großer Raum: [15,12,8,11,10,7,6,1,5,4,9,3,null,null,null,null,null,null,null,null,null,null , null,null]

Empfohlenes Lernen: „Java-Video-Tutorial“

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Prinzipien und Implementierung des minimalen und maximalen Heaps von Java-Datenstrukturen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!