Heim >Java >javaLernprogramm >Detaillierte Erläuterung des AVL-Baums der Java-Datenstruktur
Detaillierte Erläuterung des AVL-Baums der Java-Datenstruktur
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2022-06-01 11:39:052285Durchsuche
Dieser Artikel vermittelt Ihnen relevantes Wissen über Java, das hauptsächlich das relevante Wissen über ausgeglichene Binärbäume (AVL-Bäume) vorstellt. Schauen wir uns das gemeinsam an hilft allen.

Empfohlene Studie: „Java-Video-Tutorial“
Einführung des AVL-Baums
Das Durchsuchen von Binärbäumen hat eine extrem hohe Sucheffizienz, aber das Durchsuchen von Binärbäumen führt zu den folgenden Extremsituationen: 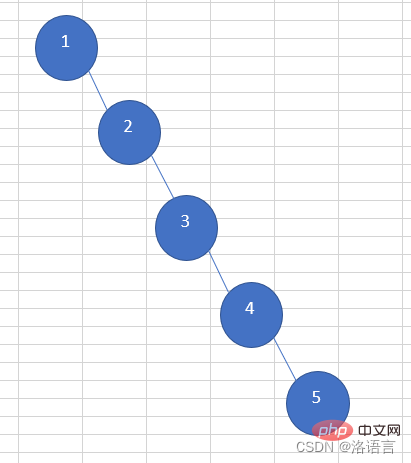
Ein solcher Binärbaum Die Sucheffizienz ist sogar geringer als bei verknüpften Listen. Der ausgeglichene Binärbaum (AVL-Baum), der basierend auf dem Suchbinärbaum erscheint, löst dieses Problem. Wenn der Absolutwert des Höhenunterschieds zwischen dem linken und dem rechten Teilbaum eines Knotens in einem ausgeglichenen Binärbaum (AVL-Baum) größer als 1 ist, wird der Höhenunterschied durch eine Rotationsoperation verringert.
Grundkonzept
Der AVL-Baum ist im Wesentlichen ein binärer Suchbaum. Seine Eigenschaften sind:
- Er selbst ist zunächst ein
binärer Suchbaum. - 每个结点的左右子树的
高度之差的绝对值(平衡因子)最多为1。也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。 - 当插入一个节点或者删除一个节点时,导致某一个节点的左右子树高度差的绝对值大于1,这时需要通过
左旋和右旋的操作使二叉树再次达到平衡状态。
二叉搜索树。平衡因子(balanceFactor)
- 一个结点的左子树与右子树的
高度之差。 - AVL树中的任意结点的BF只可能是
-1,0和1。
基础设计
下面是AVL树需要的简单方法和属性:
public class AVLTree <e>>{
class Node{
E value;
Node left;
Node right;
int height;
public Node(){}
public Node(E value){
this.value = value;
height = 1;
left = null;
right = null;
}
public void display(){
System.out.print(this.value + " ");
}
}
Node root;
int size;
public int size(){
return size;
}
public int getHeight(Node node) {
if(node == null) return 0;
return node.height;
}
//获取平衡因子(左右子树的高度差,大小为1或者0是平衡的,大小大于1不平衡)
public int getBalanceFactor(){
return getBalanceFactor(root);
}
public int getBalanceFactor(Node node){
if(node == null) return 0;
return getHeight(node.left) - getHeight(node.right);
}
//判断一个树是否是一个平衡二叉树
public boolean isBalance(Node node){
if(node == null) return true;
int balanceFactor = Math.abs(getBalanceFactor(node.left) - getBalanceFactor(node.right));
if(balanceFactor > 1) return false;
return isBalance(node.left) && isBalance(node.right);
}
public boolean isBalance(){
return isBalance(root);
}
//中序遍历树
private void inPrevOrder(Node root){
if(root == null) return;
inPrevOrder(root.left);
root.display();
inPrevOrder(root.right);
}
public void inPrevOrder(){
System.out.print("中序遍历:");
inPrevOrder(root);
}}</e>
RR(左旋)
往一个树右子树的右子树上插入一个节点,导致二叉树变得不在平衡,如下图,往平衡二叉树中插入5,导致这个树变得不再平衡,此时需要左旋操作,如下: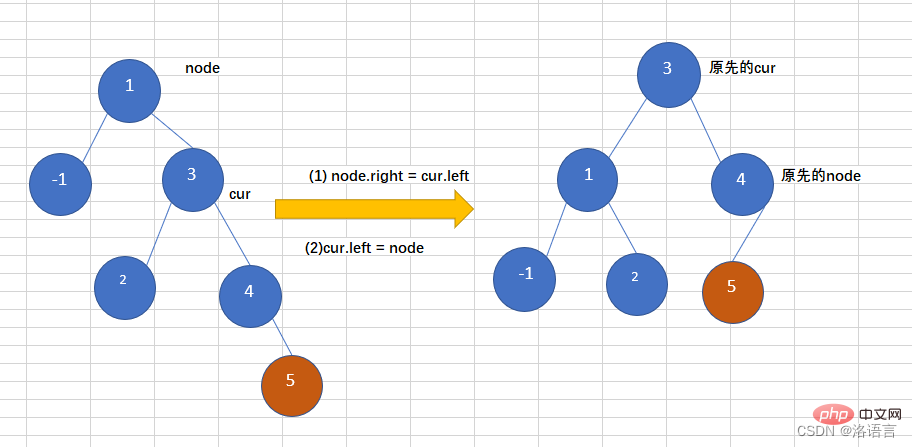
代码如下:
//左旋,并且返回新的根节点
public Node leftRotate(Node node){
System.out.println("leftRotate");
Node cur = node.right;
node.right = cur.left;
cur.left = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}
LL(右旋)
往一个AVL树左子树的左子树上插入一个节点,导致二叉树变得不在平衡,如下图,往平衡二叉树中插入2,导致这个树变得不再平衡,此时需要左旋操作,如下: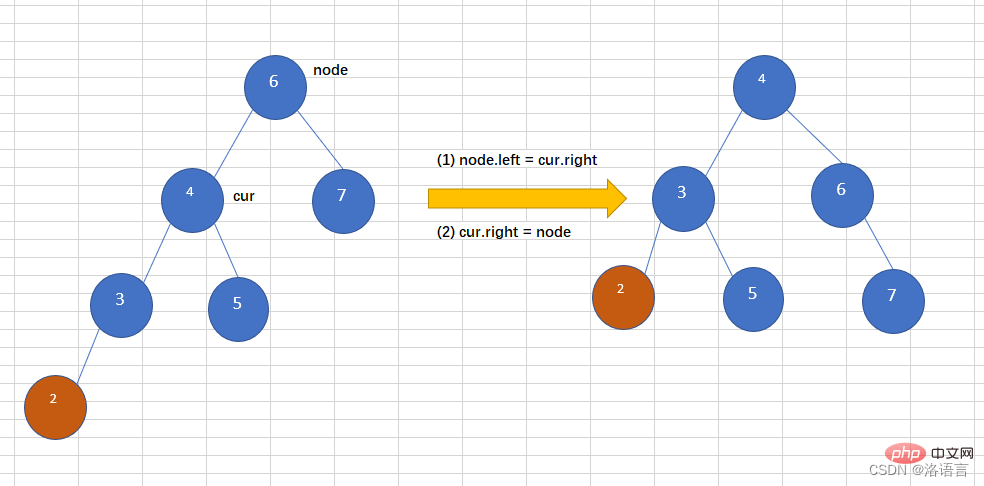
代码如下:
//右旋,并且返回新的根节点
public Node rightRotate(Node node){
System.out.println("rightRotate");
Node cur = node.left;
node.left = cur.right;
cur.right = node;
//跟新node和cur的高度
node.height = Math.max(getHeight(node.left),getHeight(node.right)) + 1;
cur.height = Math.max(getHeight(cur.left),getHeight(cur.right)) + 1;
return cur;
}
LR(先左旋再右旋)
往AVL树左子树的右子树上插入一个节点,导致该树不再平衡,需要先对左子树进行左旋,再对整棵树右旋,如下图所示,插入节点为5.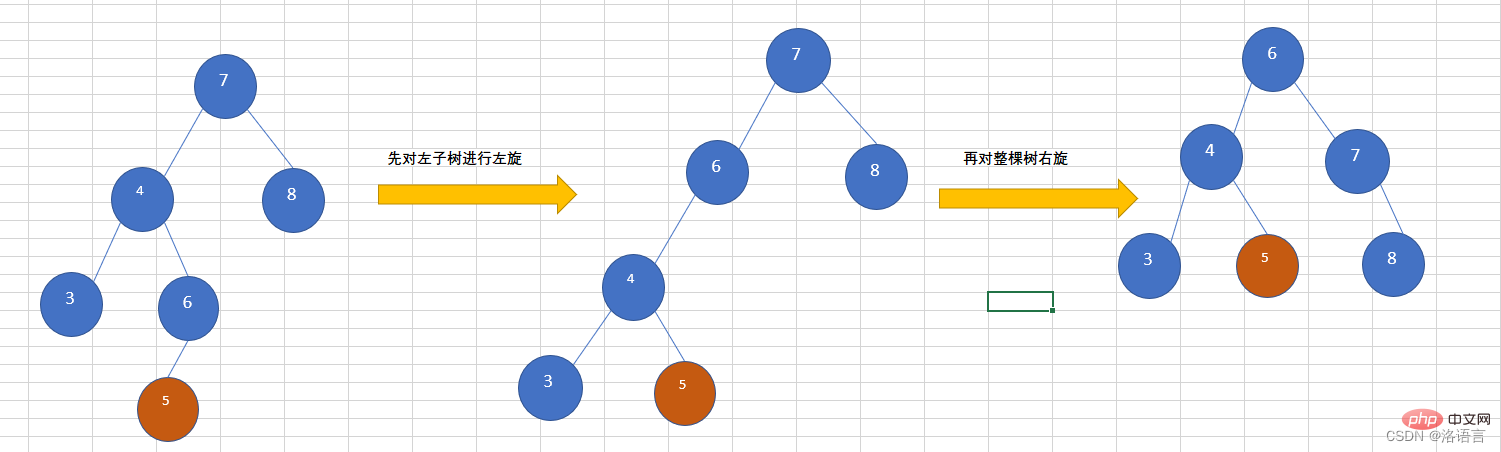
RL(先右旋再左旋)
往AVL树右子树的左子树上插入一个节点,导致该树不再平衡,需要先对右子树进行右旋,再对整棵树左旋Der absolute Wert (Balancefaktor) des Höhenunterschieds zwischen dem linken und rechten Teilbaum jedes Knotens beträgt höchstens 1. Mit anderen Worten, der AVL-Baum ist im Wesentlichen ein binärer Suchbaum (binärer Sortierbaum, binärer Suchbaum) mit Balance-Funktion.
Beim Einfügen eines Knotens oder Löschen eines Knotens ist der Absolutwert des Höhenunterschieds zwischen dem linken und dem rechten Teilbaum eines Knotens größer als 1. In diesem Fall sind Linksdrehung und Rechtsdrehung erreicht der Binärbaum wieder einen ausgeglichenen Zustand. 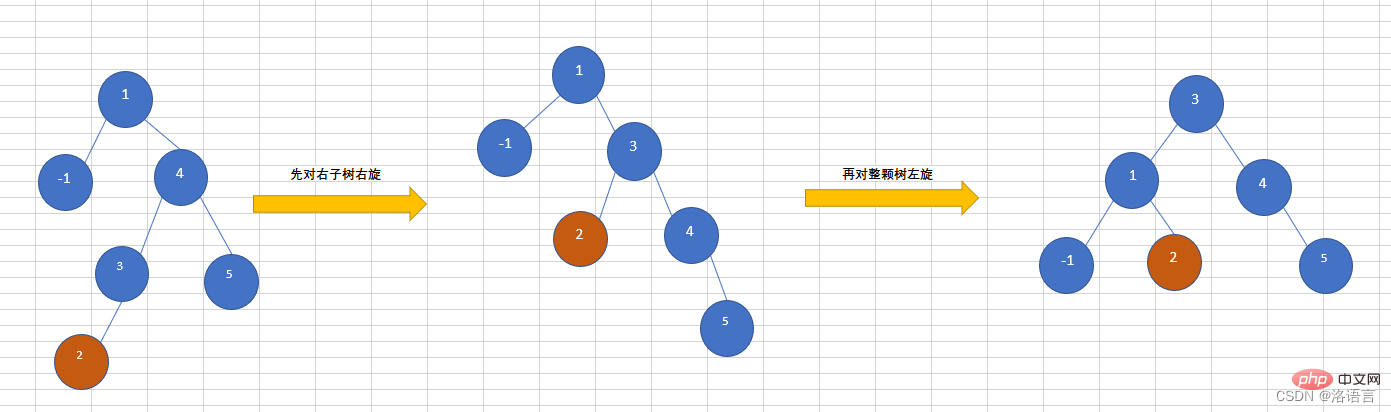 Balance Factor (balanceFactor)
Balance Factor (balanceFactor)
Der Höhenunterschied zwischen dem linken Teilbaum und dem rechten Teilbaum eines Knotens.
Der BF eines beliebigen Knotens im AVL-Baum kann nur -1, 0 und 1 sein.
Grundlegendes Design
Die folgenden einfachen Methoden und Attribute sind für den AVL-Baum erforderlich: //添加元素
public void add(E e){
root = add(root,e);
}
public Node add(Node node, E value) {
if (node == null) {
size++;
return new Node(value);
}
if (value.compareTo(node.value) > 0) {
node.right = add(node.right, value);
} else if (value.compareTo(node.value) 1 && getBalanceFactor(node.left) >= 0) {
return rightRotate(node);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上,此时需要进行左旋
else if (balanceFactor 1 && getBalanceFactor(node.left) 0
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树的左子树上,此时需要先对右子树右旋,再整个树左旋
else if(balanceFactor 0) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}RR (Linksdrehung)
//删除节点
public E remove(E value){
root = remove(root,value);
if(root == null){
return null;
}
return root.value;
}
public Node remove(Node node, E value){
Node retNode = null;
if(node == null)
return retNode;
if(value.compareTo(node.value) > 0){
node.right = remove(node.right,value);
retNode = node;
}
else if(value.compareTo(node.value) 1 && getBalanceFactor(retNode.left) >= 0) {
return rightRotate(retNode);
}
//该子树不平衡且新插入节点(导致不平衡的节点)在右子树子树的右子树上,此时需要进行左旋
else if (balanceFactor 1 && getBalanceFactor(retNode.left) 0) {
retNode.right = rightRotate(retNode.right);
return leftRotate(retNode);
}
return retNode;
}🎜 LL (Rechtsdrehung)🎜🎜In Richtung des linken Teilbaums eines AVL-Baums. Das Einfügen eines Knotens in den linken Teilbaum führt dazu, dass der Binärbaum aus dem Gleichgewicht gerät, wie in der Abbildung unten gezeigt. Das Einfügen von 2 in den ausgeglichenen Binärbaum führt dazu, dass der Baum aus dem Gleichgewicht gerät . Zu diesem Zeitpunkt ist eine Linksabbiegeoperation wie folgt erforderlich: 🎜 🎜 Der Code lautet wie folgt: 🎜rrreee🎜LR (zuerst links und dann rechts abbiegen)🎜🎜Fügen Sie einen Knoten in den
🎜 Der Code lautet wie folgt: 🎜rrreee🎜LR (zuerst links und dann rechts abbiegen)🎜🎜Fügen Sie einen Knoten in den rechten Teilbaum des linken Teilbaums des AVL-Baums ein, Dies führt dazu, dass der Baum aus dem Gleichgewicht gerät. Sie müssen zuerst eine Linksdrehung am linken Teilbaum durchführen und dann Der gesamte Baum wird nach rechts gedreht, wie in der Abbildung unten gezeigt. Der eingefügte Knoten ist 5.🎜 🎜🎜 RL (zuerst rechts abbiegen, dann links abbiegen)🎜🎜Fügen Sie einen Knoten in den
🎜🎜 RL (zuerst rechts abbiegen, dann links abbiegen)🎜🎜Fügen Sie einen Knoten in den linken Teilbaum des rechten Teilbaums ein. Dadurch ist der Baum nicht mehr ausgeglichen. Sie müssen ihn zuerst ausführen Führen Sie eine Rechtsdrehung am rechten Teilbaum durch und führen Sie dann eine Linksdrehung am gesamten Baum durch. Wie in der Abbildung unten gezeigt, ist der eingefügte Knoten 2.🎜🎜 🎜🎜 Knoten hinzufügen🎜rrreee🎜Knoten löschen🎜rrreee🎜Empfohlenes Lernen: „🎜Java-Video-Tutorial🎜“🎜Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des AVL-Baums der Java-Datenstruktur. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Machen Sie sich mit der Open-Source-Bibliothek SPL für die strukturierte Java-Datenverarbeitung vertraut
- Erweitertes JavaScript-Syntaxlernen im strikten Modus
- Eine ausführliche Einführung in gängige Grundmethoden von JavaScript-Strings
- Beherrschen Sie die String-Klasse von Java vollständig
- Grundlegende Java-Induktionsaufzählung

