Heim >Backend-Entwicklung >Python-Tutorial >Lassen Sie uns gemeinsam Anwendungen und Übungen im Zusammenhang mit der Python-Warteschlange analysieren
Lassen Sie uns gemeinsam Anwendungen und Übungen im Zusammenhang mit der Python-Warteschlange analysieren
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2022-03-30 18:35:142894Durchsuche
Dieser Artikel vermittelt Ihnen relevantes Wissen über Python, in dem hauptsächlich warteschlangenbezogene Anwendungsübungen vorgestellt werden, einschließlich der Verwendung von zwei Stapeln zur Implementierung einer Warteschlange, der Verwendung von zwei Warteschlangen zur Implementierung eines Stapels und der Stapelbeurteilung der Kontinuität von Elementen. usw. Ich hoffe, es wird für alle hilfreich sein.

Empfohlenes Lernen: Python-Tutorial
0. Lernziele
Wir haben die damit verbundenen Konzepte von Warteschlangen und deren Implementierung kennengelernt und auch die breite Anwendung von Warteschlangen bei praktischen Problemen verstanden Durch warteschlangenbezogene Übungen soll das Verständnis von Warteschlangen weiter vertieft werden. Gleichzeitig können Warteschlangen verwendet werden, um die Zeitkomplexität bei der Lösung einiger komplexer Probleme zu verringern.
1. Verwenden Sie zwei Stapel, um eine Warteschlange zu implementieren.
[Frage] Implementieren Sie bei zwei Stapeln eine Warteschlange, indem Sie nur die Grundoperationen des Stapels verwenden.
[Idee] Der Schlüssel zur Lösung dieses Problems liegt in der Umkehrfunktion des Stapels. Eine Reihe von Elementen, die auf den Stapel geschoben werden, werden in umgekehrter Reihenfolge zurückgegeben, wenn sie aus dem Stapel herausspringen. Daher kann durch die Verwendung von zwei Stapeln die Rückgabe von Elementen in derselben Reihenfolge erreicht werden (die umgekehrte Reihenfolge der Elemente wird erneut umgekehrt, um die ursprüngliche Reihenfolge zu erhalten). Die spezifische Operation ist in der folgenden Abbildung dargestellt:
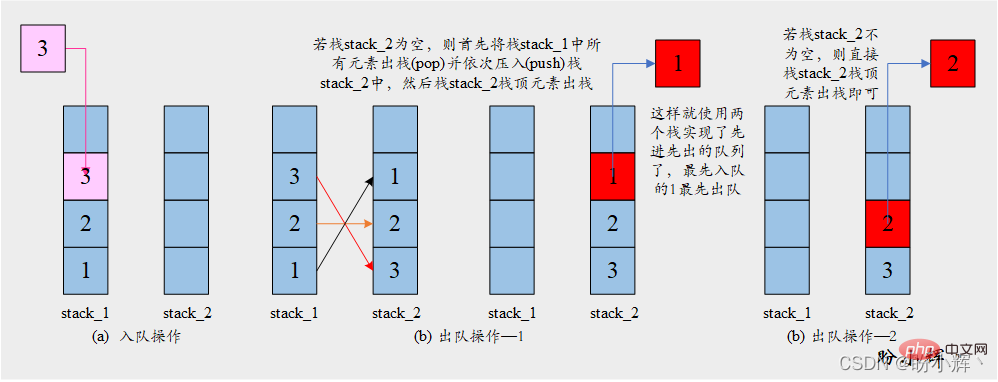
[Algorithmus]
Enqueue
enqueue:
Schieben Sie Elemente auf den Stapelstack_1
Aus der Warteschlange entfernenaus der Warteschlange:
Wenn der Stapelstack_2nicht leer ist:
Aus der Warteschlangestack_2entfernen Das oberste Element öffnen des Stapels
/> Ansonsten:
Alle Elemente ausstack_1entfernen und instack_2verschieben.
stack_2Öffnen Sie das oberste Element des Stapelsenqueue:
将元素推入栈stack_1
出队dequeue:
如果栈stack_2不为空:
stack_2栈顶元素出栈
否则:
将所有元素依次从stack_1弹出并压入stack_2
stack_2栈顶元素出栈
[代码]
class Queue: def __init__(self): self.stack_1 = Stack() self.stack_2 = Stack() def enqueue(self, data): self.stack_1.push(data) def dequeue(self): if self.stack_2.isempty(): while not self.stack_1.isempty(): self.stack_2.push(self.stack_1.pop()) return self.stack_2.pop()
[时空复杂度] 入队时间复杂度为 O(1),如果栈 stack_2 不为空,那么出队的时间复杂度为 O(1),如果栈 stack_2 为空,则需要将元素从 stack_1 转移到 stack_2,但由于 stack_2 中转移的元素数量和出队的元素数量是相等的,因此出队的摊销时间复杂度为 O(1)。
2. Lassen Sie uns gemeinsam Anwendungen und Übungen im Zusammenhang mit der Python-Warteschlange analysieren
[问题] 给定两个队列,仅使用队列的基本操作实现一个栈。
[思路] 由于队列并不具备反转顺序的特性,入队顺序即为元素的出队顺序。因此想要获取最后一个入队的元素,需要首先将之前所有元素出队。因此为了使用两个队列实现栈,我们需要将其中一个队列 store_queue 用于存储元素,另一个队列 temp_queue 则用来保存为了获取最后一个元素而保存临时出队的元素。push 操作将给定元素入队到存储队列 store_queue 中;pop 操作首先把存储队列 store_queue 中除最后一个元素外的所有元素都转移到临时队列 temp_queue 中,然后存储队列 store_queue
[Code]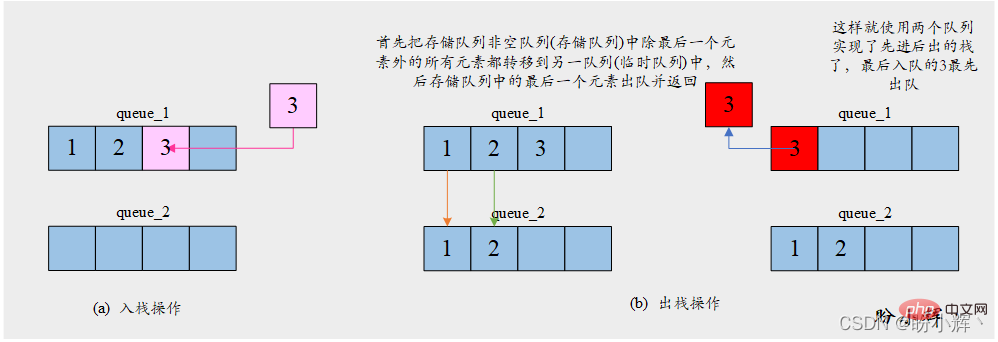
class Stack:
def __init__(self):
self.queue_1 = Queue()
self.queue_2 = Queue()
def isempty(self):
return self.queue_1.isempty() and self.queue_2.isempty()
def push(self, data):
if self.queue_2.isempty():
self.queue_1.enqueue(data)
else:
self.queue_2.enqueue(data)
def pop(self):
if self.isempty():
raise IndexError("Stack is empty")
elif self.queue_2.isempty():
while not self.queue_1.isempty():
p = self.queue_1.dequeue()
if self.queue_1.isempty():
return p
self.queue_2.enqueue(p)
else:
while not self.queue_2.isempty():
p = self.queue_2.dequeue()
if self.queue_2.isempty():
return p
self.queue_1.enqueue(p)
[Zeit- und Raumkomplexität] Die zeitliche Komplexität des Einreihens beträgt O(1) , wenn der Stapel stack_2 nicht leer ist, beträgt die zeitliche Komplexität des Entfernens aus der Warteschlange O span>(1) wenn der Stapel stack_2 leer ist, daher müssen die Elemente von stack_1 nach stack_2 übertragen werden, aber aufgrund von Die übertragenen Elemente in stack_2 Die Anzahl und die Anzahl der aus der Warteschlange entfernten Elemente sind gleich, daher beträgt die amortisierte Zeitkomplexität des Entnehmens aus der Warteschlange O(1).
store_queue zum Speichern von Elementen und die andere Warteschlange temp_queue zum Speichern der Elemente verwenden Holen Sie sich das letzte Element. Die Operation push stellt das angegebene Element in die Speicherwarteschlange store_queue ein; die Operation pop stellt das angegebene Element zunächst in die Speicherwarteschlange store_queue ein Alle Elemente außer dem letzten Element werden in die temporäre Warteschlange temp_queue übertragen, und dann wird das letzte Element in der Speicherwarteschlange store_queue aus der Warteschlange entfernt und zurückgegeben. Die spezifische Operation ist in der folgenden Abbildung dargestellt: 🎜🎜🎜🎜🎜🎜[Algorithmus]🎜🎜算法运行过程需要始终保持其中一个队列为空,用作临时队列
入栈push:在非空队列中插入元素data。
若队列queue_1为空:
将data插入 队列queue_2中
否则:
将data插入 队列queue_1中
出栈pop:将队列中的前n−1 个元素插入另一队列,删除并返回最后一个元素
若队列queue_1不为空:
将队列queue_1的前n−1 个元素插入queue_2,然后queue_1的最后一个元素出队并返回
若队列queue_2不为空:
将队列queue_2的前 n−1 个元素插入queue_1,然后queue_2的最后一个元素出队并返回
[代码]
class Stack:
def __init__(self):
self.queue_1 = Queue()
self.queue_2 = Queue()
def isempty(self):
return self.queue_1.isempty() and self.queue_2.isempty()
def push(self, data):
if self.queue_2.isempty():
self.queue_1.enqueue(data)
else:
self.queue_2.enqueue(data)
def pop(self):
if self.isempty():
raise IndexError("Stack is empty")
elif self.queue_2.isempty():
while not self.queue_1.isempty():
p = self.queue_1.dequeue()
if self.queue_1.isempty():
return p
self.queue_2.enqueue(p)
else:
while not self.queue_2.isempty():
p = self.queue_2.dequeue()
if self.queue_2.isempty():
return p
self.queue_1.enqueue(p)
[时空复杂度] push 操作的时间复杂度为O(1),由于 pop 操作时,都需要将所有元素从一个队列转移到另一队列,因此时间复杂度O(n)。
3. 栈中元素连续性判断
[问题] 给定一栈 stack1,栈中元素均为整数,判断栈中每对连续的数字是否为连续整数(如果栈有奇数个元素,则排除栈顶元素)。例如,输入栈 [1, 2, 5, 6, -5, -4, 11, 10, 55],输入为 True,因为排除栈顶元素 55 后,(1, 2)、(5, 6)、(-5, -4)、(11, 10) 均为连续整数。
[思路] 由于栈中可能存在奇数个元素,因此为了正确判断,首次需要将栈中元素反转,栈顶元素变为栈底,然后依次出栈,进行判断。
[算法]
栈
stack中所有元素依次出栈,并插入队列queue中
队列queue中所有元素出队,并入栈stack
while 栈stack不为空:
栈顶元素e1出栈,并插入队列queue中
如果栈stack不为空:
栈顶元素e2出栈,并插入队列queue中
如果|e1-e2|!=1:
返回False,跳出循环
队列queue中所有元素出队,并入栈stack
[代码]
def check_stack_pair(stack): queue = Queue() flag = True # 反转栈中元素 while not stack.isempty(): queue.enqueue(stack.pop()) while not queue.isempty(): stack.push(queue.dequeue()) while not stack.isempty(): e1 = stack.pop() queue.enqueue(e1) if not stack.isempty(): e2 = stack.pop() queue.enqueue(e2) if abs(e1-e2) != 1: flag = False break while not queue.isempty(): stack.push(queue.dequeue()) return flag
[时空复杂度] 时间复杂度为 O(n),空间复杂度为 O(n)。
4. Lassen Sie uns gemeinsam Anwendungen und Übungen im Zusammenhang mit der Python-Warteschlange analysieren
[问题] 给定一个整数队列 queue,将队列的前半部分与队列的后半部分交错来重新排列元素。例如输入队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9],则输出应为 [1, 6, 2, 7, 3, 8, 4, 9, 5]。
[思路] 通过获取队列的前半部分,然后利用栈的反转特性,可以实现重排操作,如下图所示:
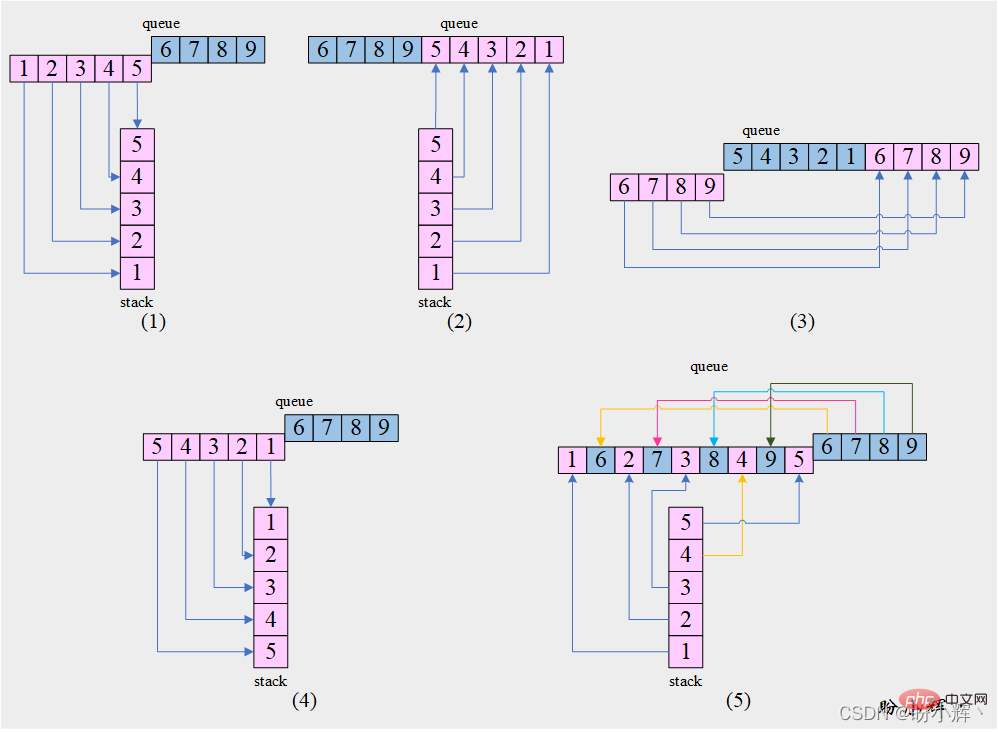
[算法]
如果队列
queue中的元素数为偶数:
half=queue.size//2
否则:
half=queue.size//2+1
1. 将队列queue的前半部分元素依次出队并入栈stack
2. 栈stack中元素出栈并入队queue
3. 将队列queue中在步骤 1中未出队的另一部分元素依次出队并插入队尾
4. 将队列queue的前半部分元素依次出队并入栈stack
5. 将栈stack和队列queue中的元素交替弹出并入队
6. 如果栈stack非空:
栈stack中元素出栈并入队
[代码]
def queue_order(queue): stack = Stack() size = queue.size if size % 2 == 0: half = queue.size//2 else: half = queue.size//2 + 1 res = queue.size - half for i in range(half): stack.push(queue.dequeue()) while not stack.isempty(): queue.enqueue(stack.pop()) for i in range(res): queue.enqueue(queue.dequeue()) for i in range(half): stack.push(queue.dequeue()) for i in range(res): queue.enqueue(stack.pop()) queue.enqueue(queue.dequeue()) if not stack.isempty(): queue.enqueue(stack.pop())
[时空复杂度] 时间复杂度为O(n),空间复杂度为 O(n)。
5. 反转队列中前 m 个元素的顺序
[问题] 给定一个整数 m 和一个整数队列 queue,反转队列中前 k 个元素的顺序,而其他元素保持不变。如 m=5,队列为 [1, 2, 3, 4, 5, 6, 7, 8, 9],算法输出为 [5, 4, 3, 2, 1, 6, 7, 8, 9]。
[思路] 结合 [问题4] 我们可以发现,此题就是 [问题4] 的前 3 步,如下图所示:
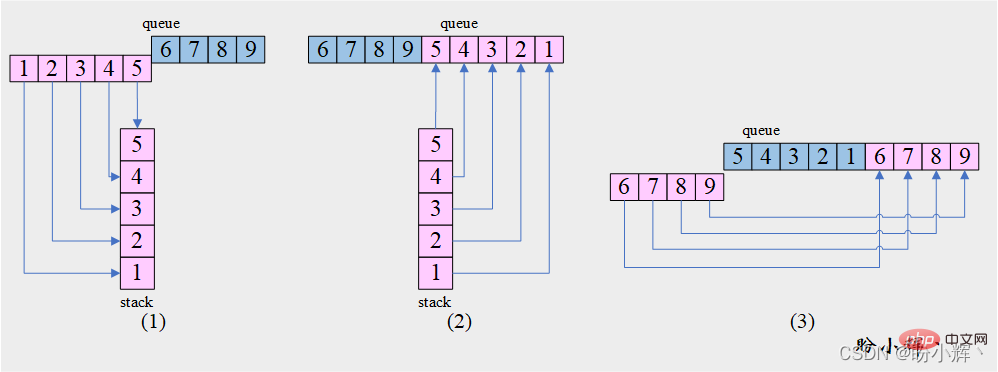
[算法]
1. 将队列
queue的前m个元素依次出队并入栈stack
2. 栈stack中元素出栈并入队queue
3. 将队列queue中在步骤 1中未出队的另一部分元素依次出队并插入队尾
[代码]
def reverse_m_element(queue, m): stack = Stack() size = queue.size if queue.isempty() or m>size: return for i in range(m): stack.push(queue.dequeue()) while not stack.isempty(): queue.enqueue(stack.pop()) for i in range(size-m): queue.enqueue(queue.dequeue())
[时空复杂度] 时间复杂度为O(n),空间复杂度为 O(n)。
Empfohlenes Lernen: Python-Tutorial
Das obige ist der detaillierte Inhalt vonLassen Sie uns gemeinsam Anwendungen und Übungen im Zusammenhang mit der Python-Warteschlange analysieren. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

