Heim >Datenbank >MySQL-Tutorial >Lassen Sie uns ausführlich darüber sprechen, warum der MySQL-Index die B+-Baumstruktur verwendet
Lassen Sie uns ausführlich darüber sprechen, warum der MySQL-Index die B+-Baumstruktur verwendet
- 青灯夜游nach vorne
- 2021-09-28 19:52:032448Durchsuche
Dieser Artikel ist eine fortgeschrittene Studie zu MySQL. Er stellt den Grund vor, warum MySQL den B+-Baum als Indexdatenstruktur verwendet.

Der Index verbessert die Abfrageeffizienz. Wenn wir direkt zu einem bestimmten Kapitel wechseln möchten, müssen wir nicht Seite für Seite umblättern. Wir müssen uns nur das Inhaltsverzeichnis ansehen und finden Sie die Seitenzahl anhand des Inhaltsverzeichnisses. [Verwandte Empfehlungen: MySQL-Video-Tutorial
Im Computer benötigen wir eine Datenstruktur zum Speichern dieses Verzeichnisses. Zu den gängigen Datenstrukturen gehören Hash-Tabellen, binäre Suchbäume, binäre ausgeglichene Bäume (AVL) und rot-schwarze Bäume. Warum wählen Innodb und MyISAM dann b+ tree? 1. Hash-TabelleEine Hash-Tabelle ist ein Array + verknüpfte Liste, wobei die Indizes 0, 1, 2, 3 ... den Speicherort ihrer Daten angeben. Wenn Sie Daten in einer Hash-Tabelle speichern möchten, verwenden Sie zunächst einen Hash-Algorithmus für die Daten (der grundlegende ist die Modulo-Operation. Wenn die Array-Länge 13 beträgt, beträgt sie nach Modulo 13 0-12, was entspricht). der untere Teil der Daten Wenn die berechneten Indizes gleich sind, wird die verknüpfte Liste an der Subskriptposition verfolgt.

- Die Verwendung von Hash-Speicher erfordert das Hinzufügen aller Datendateien zum Speicher, was mehr Speicherplatz verbraucht.
- Hash-Suche ist eine äquivalente Abfrage, die sehr schnell ist, es gibt jedoch keine Bereichsregel zwischen den einzelnen Daten. In der tatsächlichen Arbeit werden jedoch mehr Bereichsabfragen verwendet, und Hash ist nicht geeignet.
Man kann nicht direkt sagen, dass MySQL keine Hash-Tabellen verwendet, aber es muss anhand der Speicher-Engine ermittelt werden. Die Speicher-Engine verwendet Hash-Tabellen
Nachteile: 
- 3. Binär ausgeglichener Baum-AVL
Nachteile:
 1. Um das Gleichgewicht aufrechtzuerhalten, sind 1-n Rotationen erforderlich. Die Effizienz beim Einfügen und Löschen ist äußerst gering und die Abfrageeffizienz ist sehr hoch.
1. Um das Gleichgewicht aufrechtzuerhalten, sind 1-n Rotationen erforderlich. Die Effizienz beim Einfügen und Löschen ist äußerst gering und die Abfrageeffizienz ist sehr hoch.
- 4. Rot-Schwarz-Baum
Es gibt auch nur zwei Zweige, und die Tiefe wird immer noch sehr tief sein, wenn die Datenmenge groß istNachteile:

So lösen Sie das Problem, dass es nur 2 Zweige gibt und die Tiefe zu tief ist, sodass es einen B-Baum gibt , Zweige hinzufügen
5. B-Baum
Lesen Sie zuerst nicht den B-subtrahierten Baum, sondern lesen Sie den B-Baum
Alle Schlüsselwerte sind im gesamten Baum verteilt.
Die Suche endet möglicherweise an einem Nicht-Blattknoten, und eine Suche wird innerhalb des gesamten Satzes von Schlüsselwörtern durchgeführt, und die Leistung kommt der binären Suche nahe.
- Jeder Knoten hat höchstens m Teilbäume.
- Der Wurzelknoten hat mindestens 2 Teilbäume.
- Ein Zweigknoten hat mindestens m/2 Teilbäume (alle Zweigknoten außer dem Wurzelknoten und den Blattknoten).
- Alle Blattknoten befinden sich auf derselben Ebene, jeder Knoten kann bis zu m-1 Schlüssel haben und ist in aufsteigender Reihenfolge angeordnet
- Wie im Bild oben gezeigt: (Nur ein Teil des Bildes ist gezogen, tatsächlich gibt es keine Begrenzung, nicht nur p1, p2, p3)
Jeder Knoten belegt einen Plattenblock. Es gibt zwei Schlüsselwörter, die in aufsteigender Reihenfolge auf einem Knoten angeordnet sind, und drei Zeiger auf den Wurzelknoten des Unterbaums. Die Zeiger speichern die Plattenblockadresse, in der sich der untergeordnete Knoten befindet. Die drei durch die beiden Schlüsselwörter geteilten Bereichsfelder entsprechen den Bereichsfeldern der Daten des Teilbaums, auf den die drei Zeiger zeigen. Am Beispiel des Wurzelknotens lauten die Schlüsselwörter 16 und 34. Der Datenbereich des Teilbaums, auf den der p1-Zeiger zeigt, ist kleiner als 16, der Datenbereich des Teilbaums, auf den der p2-Zeiger zeigt, beträgt 16-34 und die Daten Der Bereich des Teilbaums, auf den der p3-Zeiger zeigt, ist größer als 34. .
Der Prozess zum Finden des Schlüsselworts 28:
- Finden Sie Festplattenblock 1 basierend auf dem Wurzelknoten und lesen Sie ihn in den Speicher ein. [Erster Platten-E/A-Vorgang]
- Vergleichen Sie Schlüsselwort 28 im Intervall (16, 34) und suchen Sie den Zeiger p2 von Plattenblock 1.
- Suchen Sie Festplattenblock 3 entsprechend dem p2-Zeiger und lesen Sie ihn in den Speicher ein. [Zweiter Festplatten-E/A-Vorgang]
- Vergleichen Sie Schlüsselwort 28 im Intervall (25, 31) und suchen Sie den Zeiger p2 von Festplattenblock 3.
- Finden Sie Festplattenblock 8 basierend auf Zeiger p2 und lesen Sie ihn in den Speicher. [Der dritte Festplatten-E/A-Vorgang]
- Suchen Sie das Schlüsselwort 28 in der Schlüsselwortliste in Festplattenblock 8, Ende.
Nachteile:
- Jeder Knoten hat einen Schlüssel und enthält auch Daten, und der Speicherplatz jeder Seite ist begrenzt. Wenn die Daten groß sind, wird die Anzahl der Schlüssel, die jeder Knoten speichern kann, kleiner.
- Wenn die Menge der gespeicherten Daten groß ist, nimmt die Tiefe zu, wodurch sich die Anzahl der E/A-Abfragen auf der Festplatte erhöht und somit die Abfrageleistung beeinträchtigt wird.
6. Der B+-Baum ist eine Optimierung, die auf dem B-Baum basiert. Die Änderungen sind wie folgt:
Jeder Knoten des B+-Baums kann mehrere Knoten enthalten, den ersten Grund besteht darin, die Höhe des Baums zu verringern, und der zweite Grund besteht darin, den Datenbereich in mehrere Intervalle zu ändern. Je mehr Intervalle vorhanden sind, desto schneller ist der Datenabruf.
Nicht-Blattknoten speichern nur Schlüssel, und Blattknoten speichern Schlüssel und Daten.
- Die Zeiger der Blattknoten sind miteinander verbunden (entsprechend den Merkmalen des Festplatten-Vorauslesens) und die sequentielle Abfrageleistung ist höher.
Wie im Bild oben gezeigt: Es gibt zwei Kopfzeiger im B+-Baum, einer zeigt auf den Wurzelknoten und der andere auf den kleinsten Blattknoten des Schlüsselworts, und zwischen allen Blattknoten (und Datenknoten) gibt es eine Kettenringstruktur, also B+ Baum kann sein Es gibt drei Suchvorgänge: Einer ist eine Bereichssuche und eine Paging-Suche nach dem Primärschlüssel und der andere ist eine Zufallssuche ausgehend vom Wurzelknoten.
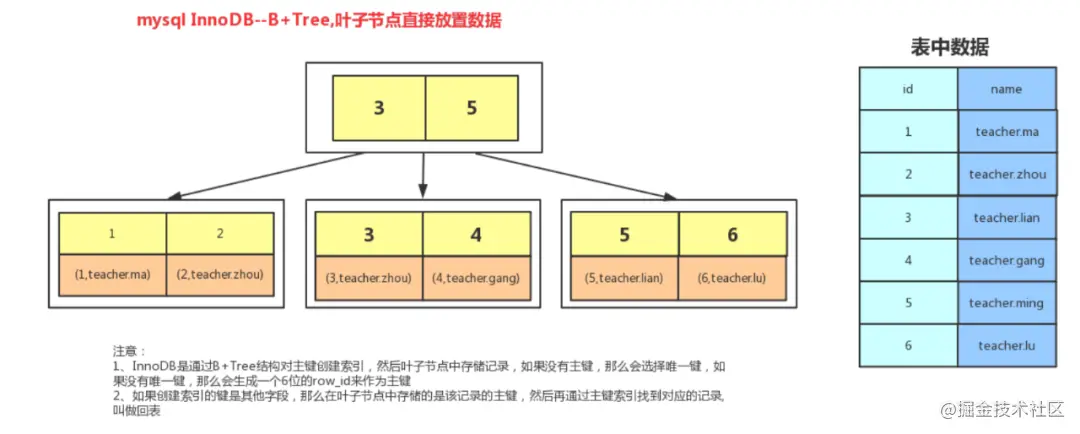
Unterschiede in den Indizes zwischen InnoDB und MyISAM1. InnoDB-PrimärschlüsselindexBlattknoten speichern bestimmte Zeilendaten2. InnoDB-Nicht-Primärschlüsselindex
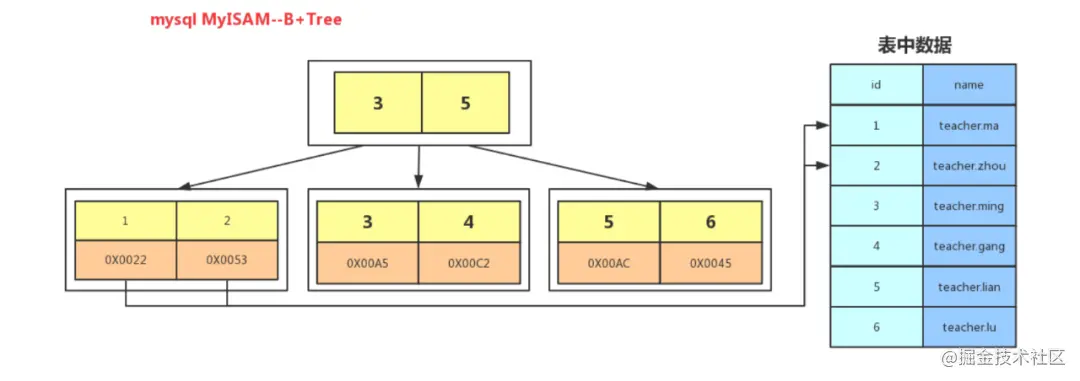
Blattknotenspeicherung von Nicht-Primärschlüsseln Indizes sind der Primärschlüsselwert (daher müssen die Abfragedaten grundsätzlich an die Tabelle zurückgegeben werden)3Die Blattknoten speichern die Adresse der Zeilendaten, was eine zusätzliche Adressierung und einen weiteren IO erfordert
Zusammenfassung: Warum MySQL den B+-Baum verwendet
Genaue Aussage: Warum die Indizes der InnoDB- und MyISAM-Speicher-Engines von MySQL den B+-Baum verwenden
Hash-Tabelle, entsprechende Abfrage ist schnell, aber nicht erfüllt allgemeine Bereichssuchen und es besteht keine Beziehung zwischen zwei benachbarten Werten, und Hashing verbraucht mehr Speicher.
Autor: Herr Ji
Binärbaum/ausgeglichener Binärbaum/Rot-Schwarz-Baum usw. haben alle nur zwei Zweige. Die Gemeinsamkeit besteht darin, dass die Tiefe des Baums und die Anzahl größer werden der IOs wird erhöht.
B-Tree speichert Daten auf den Knoten, sodass die Anzahl der auf einer Seite gespeicherten Schlüssel reduziert und die Tiefe des Baums erhöht wird.
Die Daten werden von Nicht-Blattknoten im B+-Baum entfernt, was die Anzahl der Schlüssel auf einer Seite erhöht, und die Blattknoten sind durch verknüpfte Listen verbunden, was der Bereichssuche und dem Paging förderlich ist.
Ursprüngliche Adresse: https://juejin.cn/post/6994810803643744269
Programmiervideo
Weitere Programmierkenntnisse finden Sie unter:! !
Das obige ist der detaillierte Inhalt vonLassen Sie uns ausführlich darüber sprechen, warum der MySQL-Index die B+-Baumstruktur verwendet. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- So konvertieren Sie PHP-MySQL-Zeit
- Fortgeschrittenes MySQL-Lernen: Vertiefendes Verständnis des EXPLAIN-Befehls
- MySQL Advanced Learning: Ausführliche Erklärung, wie man effiziente und geeignete Indizes erstellt
- Ein Artikel erklärt, wie man MySQL mit yum unter Linux/UNIX installiert
- Analysieren Sie anhand von Beispielen die Effizienz von or und in in MySQL