Was sind vollständige Binärbäume und Clued Binärbäume? Wie ist ihre sequentielle Speicherstruktur?

Im letzten Artikel haben wir die grundlegende Kettenstruktur von Binärbäumen und Operationen im Zusammenhang mit der Baumkonstruktion und -durchquerung kennengelernt. Heute lernen wir einige Konzepte im Zusammenhang mit Binärbäumen und einer modifizierten Form von Binärbäumen.

Vollständiger Binärbaum

Was ist ein vollständiger Binärbaum? Bevor wir über vollständige Binärbäume sprechen, sprechen wir über einen anderen Begriff: „vollständige Binärbäume“. Der Binärbaum, wie wir ihn in unserem vorherigen Artikel gezeigt haben, ist ein „vollständiger Binärbaum“. In diesem Baum haben alle Knoten zwei untergeordnete Knoten, kein Knoten hat nur einen untergeordneten Knoten und alle untersten Blattknoten befinden sich auf derselben Ebene. Diese Art von Baum wird als „Vollständiger Binärbaum“ oder „Perfekter Binärbaum“ bezeichnet Baum".

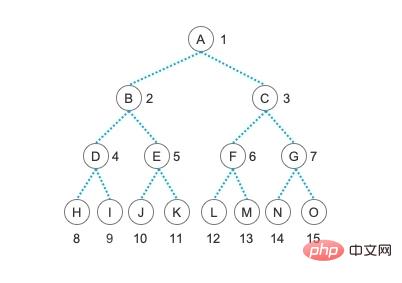
Ist das nicht ein sehr schöner Baum? Ja, diese Art von Binärbaum ist sehr perfekt. Er hat keine zusätzlichen Knoten und keine fehlenden Knoten. Er ist sehr schön. In Wirklichkeit sind perfekte Dinge jedoch sehr selten und es wird im Leben immer einige Mängel geben. Wir versuchen, nicht zu viele Mängel zuzulassen, aber wir können niemals ein Leben ohne Mängel führen. Daher lassen wir zu, dass Blattknoten auf der untersten Ebene und auf der nächstniedrigeren Ebene erscheinen, und die Blattknoten auf der untersten Ebene konzentrieren sich auf den linken Teil des Baums, das heißt, die Blattknoten können nur linke Teilbäume haben. Ein solcher Baum fehlt leicht. Der Baum wird als „vollständiger Binärbaum“ bezeichnet. Machen Sie sich keine Sorgen, dass es nicht perfekt ist, denn ein so leicht unvollkommenes Leben ist vollständig, sodass der „vollständige Binärbaum“ eine ideale Baumstruktur ist.

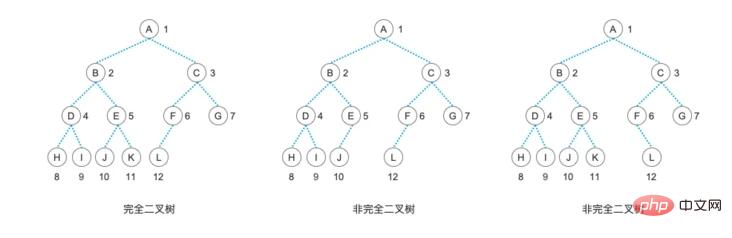
Aus der Definition können wir ersehen, dass ein „vollständiger Binärbaum“ ein „vollständiger Binärbaum“ sein muss und sich alle Blattknoten auf einer Ebene befinden und alle Knoten linke und rechte Kinder haben. Der „vollständige Binärbaum“. Der von Ihnen angeklickte Baum ist ebenfalls ein „vollständiger Binärbaum“.

Warum sprechen wir von „vollständiger Binärbaum“ und „vollständiger Binärbaum“? Natürlich soll es den Weg für unseren nächsten Inhalt ebnen. Denn ein „vollständiger Binärbaum“ ist ein Baum, der den Eigenschaften eines Binärbaums am besten entspricht. Erinnern Sie sich noch an die fünf Eigenschaften von Binärbäumen, die im ersten Artikel der Baumserie vorgestellt wurden? Zu diesem Zeitpunkt verwendeten wir zur Erläuterung den „vollständigen Binärbaum“ als Beispiel. Unter diesen ist Eigenschaft 5 die Grundlage für uns, um zu lernen, sequentielle Strukturen zum Speichern von Binärbäumen zu verwenden.

Sequentielle Speicherung von Binärbäumen

Durch das Konzept des „vollständigen Binärbaums“ und die Eigenschaft 5 von Binärbäumen können wir die Verwendung eines Arrays zum Speichern der sequentiellen Struktur implementieren.

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];

Ich glaube, Sie kennen es. Im vorherigen Artikel haben wir dieses Array verwendet, um einen Kettenbaum zu erstellen, und dieses Array ist tatsächlich ein linear gespeicherter Binärbaum. Werfen wir einen Blick darauf, indem wir Eigenschaft 5 von Binärbäumen vergleichen.

• Der Index des A-Knotens ist 1, was die Wurzel unseres Baums ist. Seine untergeordneten Knoten sind B und C, und die entsprechenden Indizes sind 2 bzw. 3, also 1 2 und 1 2 + 1.

• In ähnlicher Weise wählen wir einen anderen Knoten F aus. Sein Index ist 6, also ist der Index seines linken untergeordneten Knotens 6 2 = 12, entsprechend L, sein rechter untergeordneter Knoten ist 6 2 + 1 = 13, entsprechend M.

• Umgekehrt betrachtet ist der übergeordnete Knoten eines Knotens i / 2 . Schauen wir uns an, dass der Index des K-Knotens 11 und sein übergeordneter Knoten 11/2 ist. Wenn Sie den Dezimalpunkt weglassen, ist dies die Position des Index 5, der Knoten E ist Der übergeordnete Knoten ist 11/2. Der Knoten ist 10/2, was auch der E-Knoten mit Index 5 ist.

Jetzt denke ich, dass jeder versteht, wie man ein Array verwendet, um eine binäre Baumstruktur darzustellen. Darüber hinaus ist die Struktur des Arrays eher eindimensional, was besser widerspiegeln kann, dass die Operation des Baums eine zweidimensionale eindimensionale Darstellung ist, dh eine nichtlineare Konvertierung in eine lineare, sodass wir diese bequem bedienen können Daten.

Für sequentielle Speicherstrukturen, also das Durchlaufen von Array-Elementen, können Sie auch Vorbestellung, Mittelbestellung, Nachbestellung und hierarchische Reihenfolge verwenden. Diese Traversierungsmethoden müssen jedoch gemäß Eigenschaft 5 von Binärbäumen durchlaufen werden. Aber was noch wichtiger ist: Solange Sie mir einen Index geben, können wir über die Eigenschaften eines Binärbaums leicht die Position seiner untergeordneten und übergeordneten Knoten ermitteln und schnell die Informationen dieser Knoten erhalten. Diese Hauptfunktion ist in kettenstrukturierten Binärbäumen nicht verfügbar.

Was wäre, wenn das, was wir speichern möchten, kein „vollständiger Binärbaum“ ist? Auch wenn es sich nicht um einen vollständigen Binärbaum handelt, müssen Sie nur den entsprechenden Knoten auf einen Nullwert setzen. Zum Beispiel:

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

Das binäre Baumdiagramm, das der Struktur dieses Baums entspricht, sieht folgendermaßen aus:

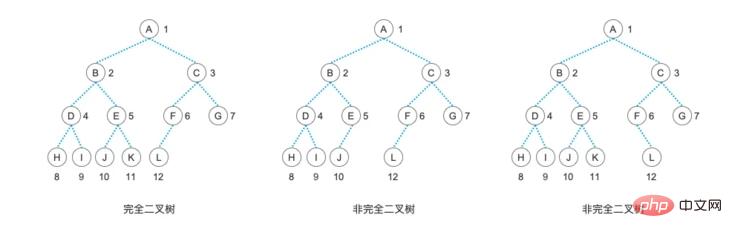
Dann müssen wir bei der Methode zum Erstellen des Kettenbaums nur noch ein weiteres Urteil hinzufügen. Durch einen solchen sequentiell gespeicherten Binärbaum können wir schnell einen verketteten Binärbaum generieren, der unsere nachfolgenden Vorgänge erleichtert.

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

Clue Binary Tree

Ein Link im anderen, lass uns als nächstes über den „Clue Binary Tree“ sprechen. Was ist das?

从上面的学习中，我们知道了”满二叉树“和”完全二叉树“。但是这种结构都是非常理想的树结构，不过真实的情况可能大部分都是”理想很丰满，现实很骨感“。很多树并不能形成那样的完全二叉树的形式，更别提”满二叉树“了。而树的遍历又经常会使用栈或者队列来实现，这两种遍历方式基本都是线性的，也就是最好情况下也是 O(n) 的时间复杂度。那么，有没有什么更快一点的方式来提高遍历的效率呢？

我们这样来尝试一下：

• 如果树的叶子结点的左孩子结点为空，就让它指向前驱（上级）结点

• 如果树的叶子结点的右孩子结点为空，就让它指向后继结点

这样有什么好处呢？我们可以避免掉大范围的递归操作，从而加快树的遍历速度。在整个算法中，它并没有什么优势，因为我们需要将一颗树进行线索化，也就是去改变它的叶子结点的左右孩子的指向，这也是一次遍历。但是，如果你的操作是经常需要遍历，而且是来回的多次遍历，那么它的整体性能是要强于普通二叉树的遍历的。因为在一次线索化之后，它的遍历就是在快速的查找叶子结点的基础上进行普通的线性遍历操作，而不是递归操作。

对于线索二叉树来说，我们需要改变树的结点存储数据结构。

// 线索二叉树结点
class TBTNode
{
    public $data;
    public $lTag = 0;
    public $rTag = 0;
    public $lChild;
    public $rChild;
}

我们增加了两个标志位，当 $lTag 或 $rTag 为 1 时，$lChild 或 $rChild 分别指向前驱或后继结点。这样在最后的遍历时，我们就可以快速地通过这个 tag 标志位分辨出结点的指向状态。

然后我们先简单地建立一颗树。使用上一节中的那个示例。

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

$tree = CreateBiTree($treeList, 1);

接下来就是最重要的线索化过程，我们可以建立前序、中序、后序的线索二叉树。对应的，在最后的线索二叉树遍历时获得的结果也将是这三种遍历方式所对应的结果。在这里，我们学习最普遍的也是最经典的”中序线索二叉树“。所以，我们以中序遍历的形式将这颗树线索化。

// 线索化
function InThread(?TBTNode $p, ?TBTNode &$pre)
{
    if ($p) {
        // 递归，左子树线索化
        InThread($p->lChild, $pre);

        if (!$p->lChild) {
            // 建立当前结点的前驱线索
            $p->lChild = $pre;
            $p->lTag = 1;
        }
        if ($pre && !$pre->rChild) {
            // 建立当前结点的后继线索
            $pre->rChild = $p;
            $pre->rTag = 1;
        }
        $pre = $p; // $pre 指向当前的 $p ，作为 $p 将要指向的下一个结点的前驱结点指示指针
        $p = $p->rChild; // $p 指向一个新结点，此时 $pre 和 $p 分别指向的结点形成了一个前驱后继对，为下一次线索化做准备
        
        // 递归，右子树线索化
        InThread($p, $pre);
    }
}

// 创建线索二叉树
function createInThread(TBTNode $root)
{
    $pre = null; // 前驱结点指针
    if($root){
        InThread($root, $pre);
        $pre->rChild = null; // 非空二叉树，线索化
        $pre->rTag = 1; // 后处理中序最后一个结点
    }
}

createInThread($tree);

var_dump($tree);
// object(TBTNode)#1 (5) {
//     ["data"]=>
//     string(1) "A"
//     ["lTag"]=>
//     int(0)
//     ["rTag"]=>
//     int(0)
//     ["lChild"]=>
//     object(TBTNode)#2 (5) {
//       ["data"]=>
//       string(1) "B"
//       ["lTag"]=>
//       int(0)
//       ["rTag"]=>
//       int(0)
//       ["lChild"]=>
//       object(TBTNode)#3 (5) {
//         ["data"]=>
//         string(1) "D"
//         ["lTag"]=>
//         int(1)
//         ["rTag"]=>
//         int(1)
//         ["lChild"]=>
//         NULL
//         ["rChild"]=>
//         *RECURSION*
//       }
//       ……

关于算法的具体步骤在注释中已经写得很详细了。一句话总结就是在中序遍历的过程中，根据结点的信息来确定它的左右孩子的形式，如果有左右孩子就继续，如果没有任一一个孩子的话，就将左右结点指向前驱或者后继。建立之后的线索二叉树就如图所示：

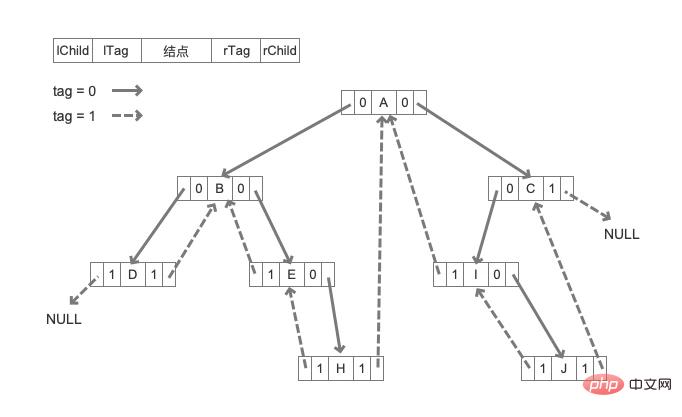
最后就是遍历了。我们需要的是能够快速地获得最左叶子结点的信息，然后就是下一跳的信息，这时，线索的威力就发挥出来了。

// 以 $p 为根的中序线索二叉树中，中序序列下的第一个结点，也就是最左边那个结点
function First(?TBTNode $p){
    while($p->lTag == 0){
        $p = $p->lChild; // 最左下结点（不一定是叶子结点）
    }
    return $p;
}

// 在中序二叉树中，结点 $p 在中序下的后继结点
function NextNode(?TBTNode $p){
    if($p->rTag == 0){
        return First($p->rChild);
    }else{
        return $p->rChild; // 如果 rTag == 1 ，直接返回后继线索
    }
}

// 在中序线索二叉树上进行中序遍历
function Inorder(TBTNode $root){
    //     第一个结点      结点不为空    下一个结点
    for($p = First($root);$p;$p=NextNode($p)){
        echo $p->data, ',';
    }
}

Inorder($tree); // D,B,E,H,A,I,J,C,

当遇到 $lTag 不为 0 的结点时，这个结点就是最左的那个结点了，如果这个不为空的话，【输出】它。接着我们获得下一跳的结点，也就是判断这个结点的右孩子 $rTag 标志，如果是为 0 的，也就是它还有右孩子，【输出】后向下查找，直到找到一个 $rTag 也为 1 的结点，直接返回这个结点的后继，也就是中序遍历的中间那个结点，【输出】它。

最后输出的顺序是不是和我们中序遍历的结果一样呢？注意看代码，在遍历中序线索二叉树的时候，我们没有用一个递归吧，全部是使用的 while() 和 for() 就完成了对这个线索二叉树的遍历。

总结

坚持到现在不容易，不能再小看数据结构了吧？现在还只是树，我们的图都还没开始呢！当然，也不要害怕，一步一步的学，慢慢掌握，不要幻想一口气吃成个胖子。写完这篇文章我也不可能马上就手写出一个中序的线索二叉树来的。大家还是以理解原理为主，如果说真能手写的话，那也是为了面试而去背的或者是为了考研而准备的。这样的小同学在面试中我反而要更多问一些其它的问题，毕竟临时抱佛脚的准备远不如深入理解带来的感悟更能打动人！

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.3完全二叉树、线索二叉树及树的顺序存储结构.php

推荐学习：php视频教程

Das obige ist der detaillierte Inhalt vonWas sind vollständige Binärbäume und Clued Binärbäume? Wie ist ihre sequentielle Speicherstruktur?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!