Detaillierte Erklärung der Warteschlangen in PHP

Heute lernen wir einen weiteren sehr klassischen logischen Strukturtyp kennen: Warteschlange. Ich glaube, dass viele Studenten bereits Cache-Warteschlangen-Tools wie Redis und RabbitMQ verwendet haben. Tatsächlich können Datenbanken und Programmcodes alle Warteschlangenoperationen implementieren. Genau wie Stapel haben auch Warteschlangen ihre eigenen spezifischen Regeln. Solange sie diesen Regeln entsprechen, wird sie als Warteschlange bezeichnet.

Was ist eine Warteschlange?

Im Vergleich zum Stapel ist die Warteschlange eine sequentielle logische FIFO-Struktur (First In First Out). Was ist First-In-First-Out? Genauso wie unsere Warteschlange, wenn wir zur Bank oder zum Krankenhaus gehen, müssen wir immer eine Nummer an der Tür nehmen, und diese Nummer wird der Reihe nach angerufen. Die Person, die zuerst kommt, kann zuerst Geschäfte machen oder einen Arzt aufsuchen. Dies ist eine typische Warteschlange. Ebenso ist die tägliche Warteschlange ein Standard-Warteschlangenmodus.

Wenn es jemanden gibt, der die Warteschlange überspringt, können wir davon ausgehen, dass er eine höhere Priorität hat, wenn es einen legitimen Grund gibt. Dies ist eine besondere Form von Elementen in der Warteschlange. So wie wir schwangeren Frauen beim Warten auf die U-Bahn oder den Bus Vorrang einräumen, gibt es auch für Militärangehörige beim Kauf von Bahntickets ein Vorrangfenster. Diesmal liegt dies jedoch außerhalb des Rahmens unserer Diskussion.

Beim Anstehen an einer Bushaltestelle darf natürlich die erste Person in der Schlange zuerst in den Bus einsteigen und so weiter. Zu diesem Zeitpunkt kommen Sie zur Bushaltestelle und können dann nur der letzte in der Schlange sein. Dies ist die spezifische Manifestation der Warteschlange.

Ähnlich wie bei Stapeln gibt es einige Substantive, die wir verstehen müssen. Wenn Sie an einer Bushaltestelle ankommen und die letzte Person in der Warteschlange sind, wird dieser Vorgang als „Einreihen in die Warteschlange“ bezeichnet. Wenn der Bus in den Bahnhof einfährt und der erste Fahrgast einsteigt, nennt man diesen Vorgang „Aussteigen“. Die Position des ersten Passagiers wird als „Kopf der Warteschlange“ bezeichnet. Als letzter Passagier in der aktuellen Warteschlange wird Ihre Position als „Ende der Warteschlange“ bezeichnet. Zurück zur Codelogik: Die Warteschlange wird am „Ende“ „betreten“ und am „Kopf“ „verlassen“.

Sequential Queue

OK, schauen wir uns den Code direkt an. Das erste, was wir sehen, ist immer noch die Implementierung der sequentiellen Warteschlange.

class SqQueue{
    public $data;
    public $front;
    public $rear;
}

Da es sich um ein sequentielles Team handelt, verwenden wir immer noch Array-Daten, um die Elemente im Team darzustellen. Definieren Sie dann zwei Zeiger vorne und hinten, um den Kopf und den Schwanz des Teams darzustellen. Da es sich um eine sequentielle Warteschlange handelt, speichert der Zeiger hier tatsächlich den Index des Arrays. Der nächste Vorgang ist eigentlich sehr einfach: Rear++ wird beim „Eintreten in die Warteschlange“ und Front++ beim „Entnehmen aus der Warteschlange“ verwendet.

function InitSqQueue(){
    $queue = new SqQueue();
    $queue->data = [];
    $queue->front = 0;
    $queue->rear = 0;
    return $queue;
}

function EnSqQueue(SqQueue &$queue, $e){
    $queue->data[$queue->rear] = $e;
    $queue->rear ++;
}

function DeSqQueue(SqQueue &$queue){
    // 队列为空
    if($queue->front == $queue->rear){
        return false;
    }
    $e = $queue->data[$queue->front];
    $queue->front++;
    return $e;
}

$q = InitSqQueue();
EnSqQueue($q, 'A');
EnSqQueue($q, 'B');
print_r($q);
// SqQueue Object
// (
//     [data] => Array
//         (
//             [0] => A
//             [1] => B
//         )

//     [front] => 0
//     [rear] => 2
// )

Haben Sie das Gefühl, dass die Warteschlange nach dem Erlernen des Stapels auch leicht zu verstehen ist? Setzen Sie beim Initialisieren der Warteschlange einfach die Kopf- und Endzeiger auf Datensätze mit 0 Indizes. Lassen Sie beim Beitreten zur Warteschlange das Ende der Warteschlange wachsen. In diesem Code fügen wir zwei Elemente der Warteschlange hinzu, und der gedruckte sequentielle Warteschlangeninhalt ist wie in den Kommentaren gezeigt.

EnSqQueue($q, 'C');
EnSqQueue($q, 'D');
EnSqQueue($q, 'E');
print_r($q);
// SqQueue Object
// (
//     [data] => Array
//         (
//             [0] => A
//             [1] => B
//             [2] => C
//             [3] => D
//             [4] => E
//         )

//     [front] => 0
//     [rear] => 5
// )

echo DeSqQueue($q), PHP_EOL; // A
echo DeSqQueue($q), PHP_EOL; // B
echo DeSqQueue($q), PHP_EOL; // C
echo DeSqQueue($q), PHP_EOL; // D
echo DeSqQueue($q), PHP_EOL; // E

echo DeSqQueue($q), PHP_EOL; // 

print_r($q);
// SqQueue Object
// (
//     [data] => Array
//         (
//             [0] => A
//             [1] => B
//             [2] => C
//             [3] => D
//             [4] => E 
//         )

//     [front] => 5
//     [rear] => 5
// )

Wenn Sie das Team verlassen, lassen Sie Front den Vorgang des Hinzufügens von 1 durchführen. Beim Entfernen aus der Warteschlange müssen Sie jedoch noch feststellen, ob alle Elemente im Array entfernt wurden. Hier verwenden wir nur eine sehr einfache Beurteilungsbedingung, nämlich ob vorne und hinten gleich sind, um festzustellen, ob die Warteschlange leer ist. Sie können eine Illustration verwenden, um das Verständnis des Codes zu erleichtern.

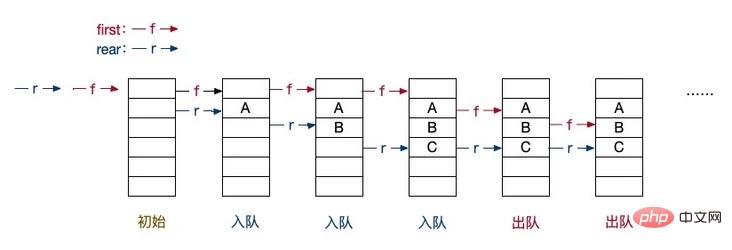
Circular Queue

Ich glaube, viele Schüler haben es bemerkt. Die Warteschlangenoperation ändert nur die Zeigerdatensätze des Warteschlangenkopfes und des Warteschlangenendes, aber das Array nimmt weiter zu. Wenn es weiter zunimmt, wird das Array den Speicher füllen. Dies ist definitiv keine gute Warteschlangenimplementierung. Tatsächlich wird Arrays in der Sprache C eine feste Länge zugewiesen. Das Array in PHP ähnelt eher einer Hash-Struktur, sodass es unendlich wachsen kann und wir zu Beginn keine bestimmte Array-Länge definieren müssen.

Das ist auch der Komfort von PHP, aber was sollen wir tun, wenn wir keinen Speicherplatz verschwenden wollen? Genau wie in der C-Sprache geben wir auch in PHP eine Länge für das Array an und verwenden eine sehr klassische „zirkuläre Warteschlange“, um das Speicherproblem des Warteschlangenarrays zu lösen. Wie im Bild unten gezeigt:

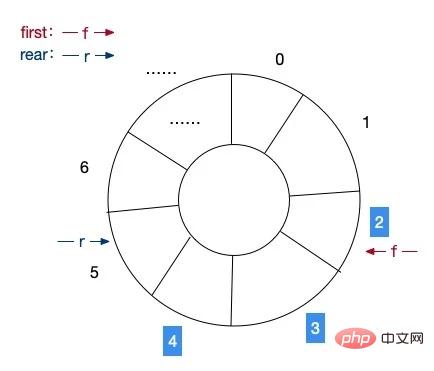
Tatsächlich bedeutet dies, dass innerhalb des begrenzten Array-Speicherplatzes die neuen Daten an der vorherigen tiefgestellten Position gespeichert werden, wenn wir den Maximalwert des Arrays erreichen. Im Bild haben wir beispielsweise 6 Elemente, der aktuelle Kopf des Teams befindet sich bei Index 2 und der Schwanz des Teams befindet sich bei Index 5. Wenn wir ein Element in die Warteschlange stellen, wird das Ende der Warteschlange auf Index 6 verschoben. Wenn Sie ein weiteres Element hinzufügen, wird das Ende der Warteschlange wieder auf den Index 0 verschoben. Wenn Sie mit dem Hinzufügen fortfahren und der Index des Endes der Warteschlange gleich dem Index des Warteschlangenkopfes minus 1 ist, gehen wir davon aus, dass die Warteschlange voll ist und keine weiteren Elemente vorhanden sind können hinzugefügt werden.

In ähnlicher Weise bedienen wir beim Entfernen aus der Warteschlange auch das Teamkopfelement zyklisch. Wenn das Teamkopfelement den Index 6 erreicht und wir es weiter aus der Warteschlange entfernen, kehrt es zur Position 0 zurück und wird weiterhin aus der Warteschlange entfernt. Wenn der Kopf der Warteschlange und das Ende der Warteschlange gleich sind, kann die aktuelle Warteschlange auch als leere Warteschlange bestimmt werden.

由此，我们可以看出，循环队列相比普通的线性队列来说，多了一个队满的状态。我们还是直接从代码中来看看这个队满的条件是如何判断的。

define('MAX_QUEUE_LENGTH', 6);

function EnSqQueueLoop(SqQueue &$queue, $e){
    // 判断队列是否满了
    if(($queue->rear + 1) % MAX_QUEUE_LENGTH == $queue->front){
        return false;
    }
    $queue->data[$queue->rear] = $e;
    $queue->rear = ($queue->rear + 1) % MAX_QUEUE_LENGTH; // 改成循环下标
}

function DeSqQueueLoop(SqQueue &$queue){
    // 队列为空
    if($queue->front == $queue->rear){
        return false;
    }
    $e = $queue->data[$queue->front];
    $queue->front = ($queue->front + 1) % MAX_QUEUE_LENGTH; // 改成循环下标
    return $e;
}

$q = InitSqQueue();
EnSqQueueLoop($q, 'A');
EnSqQueueLoop($q, 'B');
EnSqQueueLoop($q, 'C');
EnSqQueueLoop($q, 'D');
EnSqQueueLoop($q, 'E');

EnSqQueueLoop($q, 'F');

print_r($q);
// SqQueue Object
// (
//     [data] => Array
//         (
//             [0] => A
//             [1] => B
//             [2] => C
//             [3] => D
//             [4] => E
//             [5] =>   // 尾
//         )

//     [front] => 0
//     [rear] => 5
// )

echo DeSqQueueLoop($q), PHP_EOL;
echo DeSqQueueLoop($q), PHP_EOL;
print_r($q);
// SqQueue Object
// (
//     [data] => Array
//         (
//             [0] => A
//             [1] => B
//             [2] => C // 头
//             [3] => D
//             [4] => E
//             [5] =>   // 尾
//         )

//     [front] => 2
//     [rear] => 5
// )

EnSqQueueLoop($q, 'F');
EnSqQueueLoop($q, 'G');

EnSqQueueLoop($q, 'H');
print_r($q);
// SqQueue Object
// (
//     [data] => Array
//         (
//             [0] => G
//             [1] => B // 尾
//             [2] => C // 头
//             [3] => D
//             [4] => E
//             [5] => F
//         )

//     [front] => 2
//     [rear] => 1
// )

出、入队的下标移动以及队满的判断，都是以 (queue->rear + 1) % MAX_QUEUE_LENGTH 这个形式进行的。根据队列长度的取模来获取当前的循环下标，是不是非常地巧妙。不得不感慨先人的智慧呀！当然，这也是基本的数学原理哦，所以，学习数据结构还是要复习一下数学相关的知识哦！

链式队列

顺序队列有没有看懵？没关系，队列的链式结构其实相比顺序结构还要简单一些，因为它真的只需要操作队头和队尾的指针而已，别的真的就不太需要考虑了。而且这个指针就是真的指向具体对象的指针了。

class LinkQueueNode{
    public $data;
    public $next;
}

class LinkQueue{
    public $first; // 队头指针
    public $rear; // 队尾指针
}

这里我们需要两个基本的物理结构。一个是节点 Node ，一个是队列对象，节点对象就是一个正常的链表结构，没啥特别的。而队列对象里面就更简单了，一个属性是队头指针，一个属性是队尾指针。

function InitLinkQueue(){
    $node = new LinkQueueNode();
    $node->next = NULL;
    $queue = new LinkQueue();
    $queue->first = $node;
    $queue->rear = $node;
    return $queue;
}

function EnLinkQueue(LinkQueue &$queue, $e){
    $node = new LinkQueueNode();
    $node->data = $e;
    $node->next = NULL;

    $queue->rear->next = $node;
    $queue->rear = $node;
}

function DeLinkQueue(LinkQueue &$queue){
    if($queue->front == $queue->rear){
        return false;
    }

    $node = $queue->first->next;
    $v = $node->data;

    $queue->first->next = $node->next;
    if($queue->rear == $node){
        $queue->rear = $queue->first;
    }

    return $v;
}

$q = InitLinkQueue();
EnLinkQueue($q, 'A');
EnLinkQueue($q, 'B');
EnLinkQueue($q, 'C');
EnLinkQueue($q, 'D');
EnLinkQueue($q, 'E');

print_r($q);
// LinkQueue Object
// (
//     [first] => LinkQueueNode Object
//         (
//             [data] => 
//             [next] => LinkQueueNode Object
//                 (
//                     [data] => A
//                     [next] => LinkQueueNode Object
//                         (
//                             [data] => B
//                             [next] => LinkQueueNode Object
//                                 (
//                                     [data] => C
//                                     [next] => LinkQueueNode Object
//                                         (
//                                             [data] => D
//                                             [next] => LinkQueueNode Object
//                                                 (
//                                                     [data] => E
//                                                     [next] => 
//                                                 )

//                                         )

//                                 )

//                         )

//                 )

//         )

//     [rear] => LinkQueueNode Object
//         (
//             [data] => E
//             [next] => 
//         )

// )

echo DeLinkQueue($q), PHP_EOL; // A
echo DeLinkQueue($q), PHP_EOL; // B

EnLinkQueue($q, 'F');
print_r($q);
// LinkQueue Object
// (
//     [first] => LinkQueueNode Object
//         (
//             [data] => 
//             [next] => LinkQueueNode Object
//                 (
//                     [data] => C
//                     [next] => LinkQueueNode Object
//                         (
//                             [data] => D
//                             [next] => LinkQueueNode Object
//                                 (
//                                     [data] => E
//                                     [next] => LinkQueueNode Object
//                                         (
//                                             [data] => F
//                                             [next] => 
//                                         )

//                                 )

//                         )

//                 )

//         )

//     [rear] => LinkQueueNode Object
//         (
//             [data] => F
//             [next] => 
//         )

// )

出、入队的代码函数和测试代码就一并给出了，是不是非常的简单。初始的队头元素依然是一个空节点做为起始节点。然后入队的时候，让 rear 等于新创建的这个节点，并在链表中建立链式关系。出队的时候也是同样的让 first 变成当前这个 first 的下一跳节点，也就是 first->next 就可以了。判断队空的条件也是简单的变成了队头和队尾指针是否相等就可以了。链队相比顺序队其实是简单了一些，不过同样的，next 这个东西容易让人头晕，硬记下来就可以了。大家还是可以结合图示来学习：

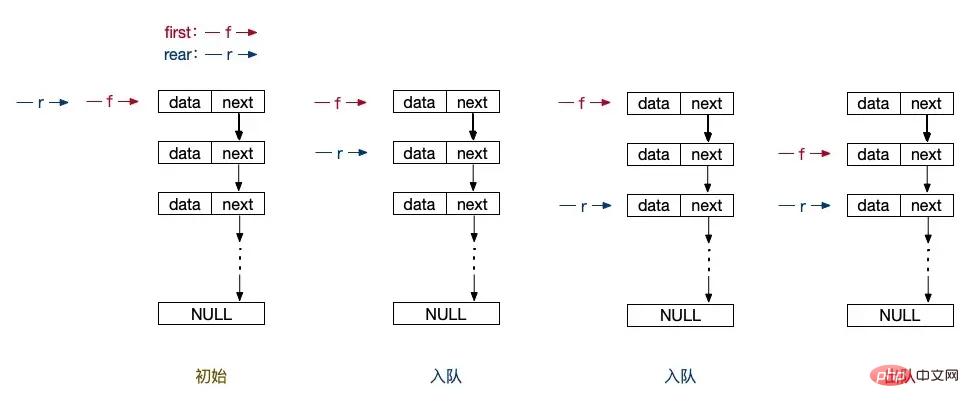
PHP 为我们提供的数组队列操作

最后，就和栈一样，PHP 代码中也为我们提供了一个可以用于队列操作的函数。

$sqQueueList = [];

array_push($sqQueueList, 'a');
array_push($sqQueueList, 'b');
array_push($sqQueueList, 'c');

print_r($sqQueueList);
// Array
// (
//     [0] => a
//     [1] => b
//     [2] => c
// )

array_shift($sqQueueList);
print_r($sqQueueList);
// Array
// (
//     [0] => b
//     [1] => c
// )

array_shift() 函数就是弹出数组中最前面的那个元素。请注意，这里元素的下标也跟着变动了，如果我们是 unset() 掉数组的 0 下标元素的话，b 和 c 的下标依然还会是 1 和 2 。而 array_shift() 则会重新整理数组，让其下标依然有序。

unset($sqQueueList[0]);
print_r($sqQueueList);
// Array
// (
//     [1] => c
// )

总结

关于栈的队列的内容我们就通过两篇文章介绍完了。不过光说不练假把式，接下来，我们来一点真实的干货，使用栈和队列来做做题呗，学算法就得刷题，一日不刷如隔三秋呀！！！

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/3.栈和队列/source/3.2队列的相关逻辑操作.php

推荐学习：php视频教程

Das obige ist der detaillierte Inhalt vonDetaillierte Erklärung der Warteschlangen in PHP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!