Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert

                                                                                                                天 Gestern habe ich einen Tag lang den Algorithmus von Hanno Tower studiert und hatte das Gefühl, dass mein IQ nicht so gut war wie der des Orang-Utans in „The Rise of the Gorilla Ball“! ! !

HerkunftEs wird gesagt, dass die Person, die dieses Problem zuerst erfunden hat, der französische Mathematiker „Edward Lucas“ war.

Im heiligen Tempel von Benares (in Nordindien) im Zentrum der Welt sind drei Edelsteinnadeln auf einer Messingplatte eingesetzt. Als Brahma, der Hauptgott des Hinduismus, die Welt erschuf, fädelte er 64 Goldstücke von unten nach oben auf eine der Nadeln. Dies ist der sogenannte Turm von Hanoi. Egal Tag oder Nacht, es gibt immer einen Mönch, der diese Goldstücke nach den folgenden Regeln bewegt: Bewegen Sie jeweils nur ein Stück, egal auf welcher Nadel es sich befindet, das kleine Stück muss über dem großen Stück liegen. Die Mönche sagten voraus, dass, wenn alle Goldstücke von der von Brahma eingefädelten Nadel auf eine andere Nadel übertragen werden, die Welt durch einen Blitz ausgelöscht wird und auch der Vatikanturm, die Tempel und alle Lebewesen gemeinsam zugrunde gehen werden.

Es gibt viele Variationen dieser Legende und es ist unbekannt, wer es ist, aber die zurückgelassenen mathematischen Probleme sind sehr klassisch.

Das mathematische Wissen, das er hinterlassen hat: Die Beziehung zwischen der Anzahl der Goldstücke und der Anzahl der Bewegungsschritte beträgt 2^n - 1.

Die Anzahl der Züge von 1 Goldstück hoch 2 minus 12^n - 1。

• 1个金片的移动次数 2的1次方减1
• 2个金片的移动次数 2的2次方减1
• 3个金片的移动次数 2的3次方减1
• …
• 个金片的移动次数 2的n次方减1

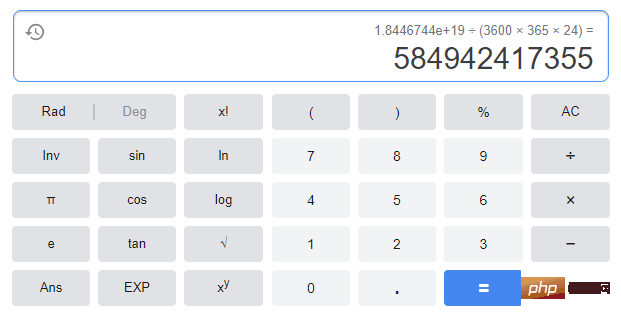
若传说属实，僧侣们需要 2^64 - 1 步才能完成这个任务；假设他们每秒移动一个金片，就需要 5849 亿年才能完成。整个宇宙现在也不过 137 亿年，所以宇宙毁灭还早…（闲的无聊，我还真计算了一下，如下图）



基本规则

汉诺塔算法有2个基本条件，假设移动的是盘子。

1.每次只能移动一个盘子。
2.小盘子必须要在大盘子的上面。

分析

假设本次游戏有3根柱子，分别是 A， B， C。其中一根上已经有排序好的盘子N个，最大的在最下面，依次向上盘子越来越小，另外2根空柱子。

Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert如下图：



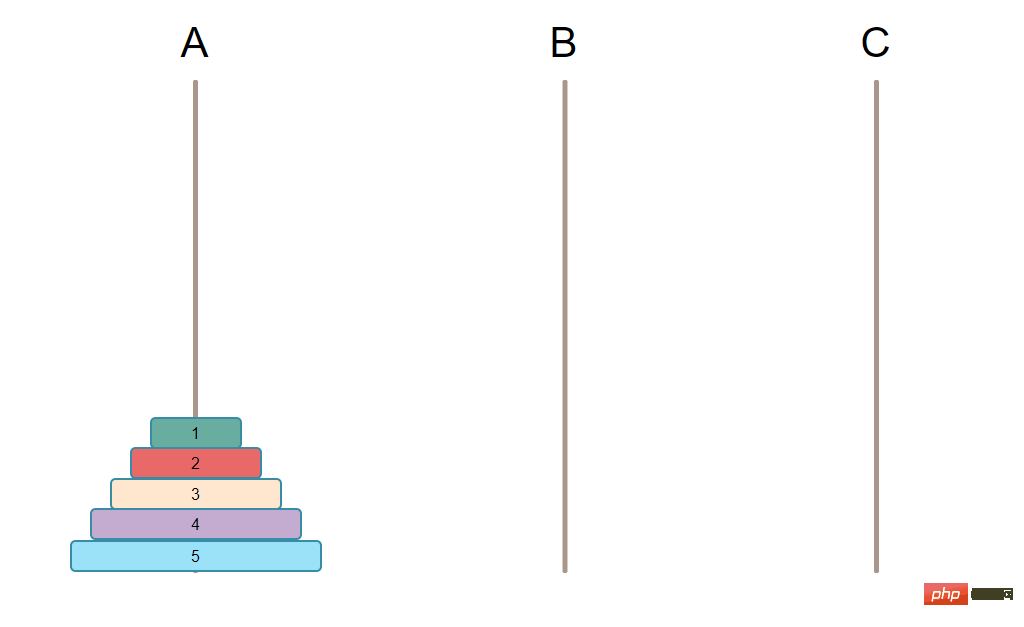
需要实现的最终目标是把柱子上所有的盘子都移动到另外一根柱子上。【推荐学习：PHP视频教程】



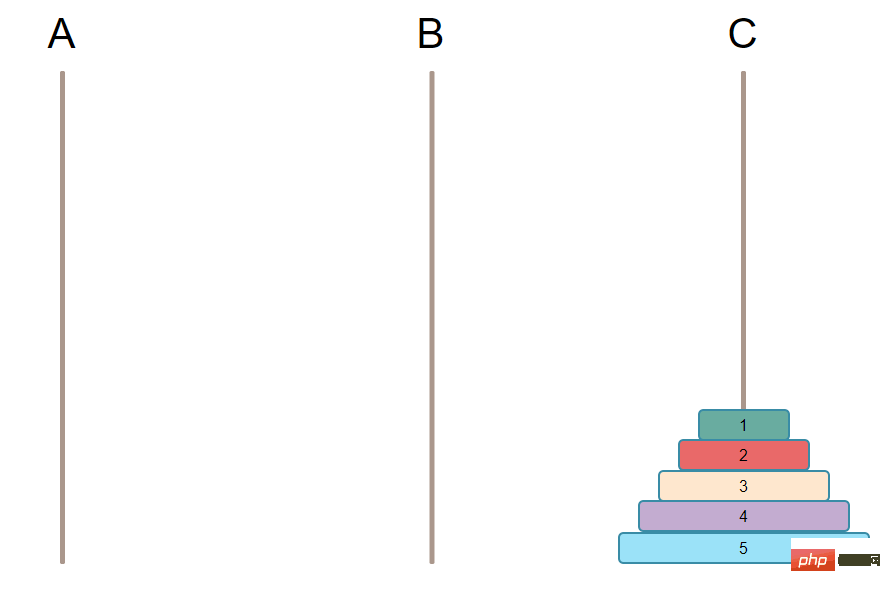
实现的大概思路：

• 抛开脑子里想着的每一步要怎么走，这个很复杂，脑容量估计不够，先想最简单粗暴的解决逻辑。
• 要满足大盘子在下的基本条件，肯定需要先把A上最大的盘子空出来，然后把最大的盘子放到C柱子上。假设最大的盘子编号是N。
• 因为要移动到C，要实现Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert，肯定需要把 N-1 个盘子都搬移到B柱子上，只有这样第N个盘子（也就是最大的盘子）才能移动到C柱子上。
• 把 N-1 个盘子移动到B柱子上，因为要满足条件大的在下，小的在上，所以这 N-1
Die Anzahl der Züge von 2 Goldstücken hoch 2 minus 1
• Die Anzahl der Züge von 3 Goldstücken hoch von 2 minus 3 1

…

Die Anzahl der Züge von 2 Goldstücken zur n-ten Potenz minus 1

Wenn die Legende wahr ist, benötigen die Mönche 2^64 - 1 Schritte zu Unter der Annahme, dass sie jeweils ein Goldstück pro Sekunde bewegen, würde es 584,9 Milliarden Jahre dauern. Das gesamte Universum ist erst 13,7 Milliarden Jahre alt, daher ist es noch früh für die Zerstörung des Universums ... (Mir war langweilig, also habe ich tatsächlich die Berechnung durchgeführt, wie unten gezeigt)


Grundregeln

Der Tower of Hanoi-Algorithmus hat zwei Grundbedingungen, vorausgesetzt dass die Platte bewegt wird. 1. Es kann jeweils nur eine Platte bewegt werden.
2. Der kleine Teller muss auf dem großen Teller liegen.

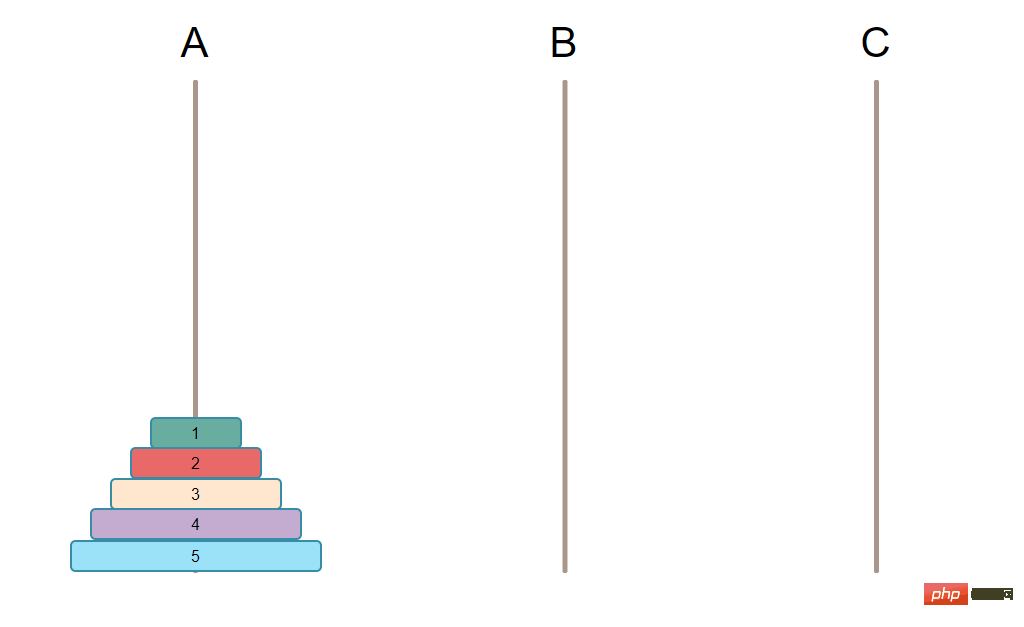🎜🎜🎜Analyse🎜🎜Angenommen, es gibt drei Säulen in diesem Spiel, nämlich A, B und C. Auf einer davon befinden sich bereits N sortierte Platten, die größte befindet sich unten, und nach oben werden die Platten immer kleiner, und es gibt zwei weitere leere Spalten. 🎜🎜Der Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert ist wie folgt: 🎜🎜🎜🎜 Das ultimative Ziel, das erreicht werden muss, besteht darin, alle Platten auf der Säule auf eine andere Säule zu verschieben. [Empfohlenes Lernen: PHP-Video-Tutorial]🎜🎜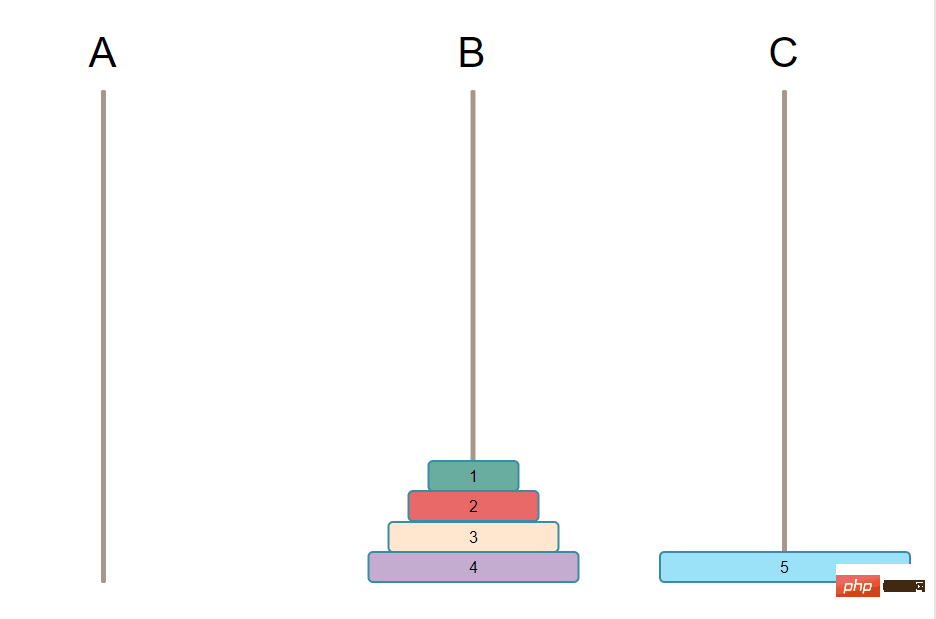🎜🎜Über die Umsetzungsidee: 🎜
🎜Beiseite werfen I Ich denke darüber nach, wie ich jeden Schritt ausführen soll. Ich glaube nicht, dass meine Gehirnkapazität ausreicht. Ich möchte zuerst über die einfachste und gröbste Lösungslogik nachdenken. 🎜🎜Um die Grundvoraussetzung zu erfüllen, dass der große Teller unten ist, müssen Sie zuerst den größten Teller auf A leeren und dann den größten Teller auf Säule C stellen. Angenommen, die größte Plattennummer ist N. 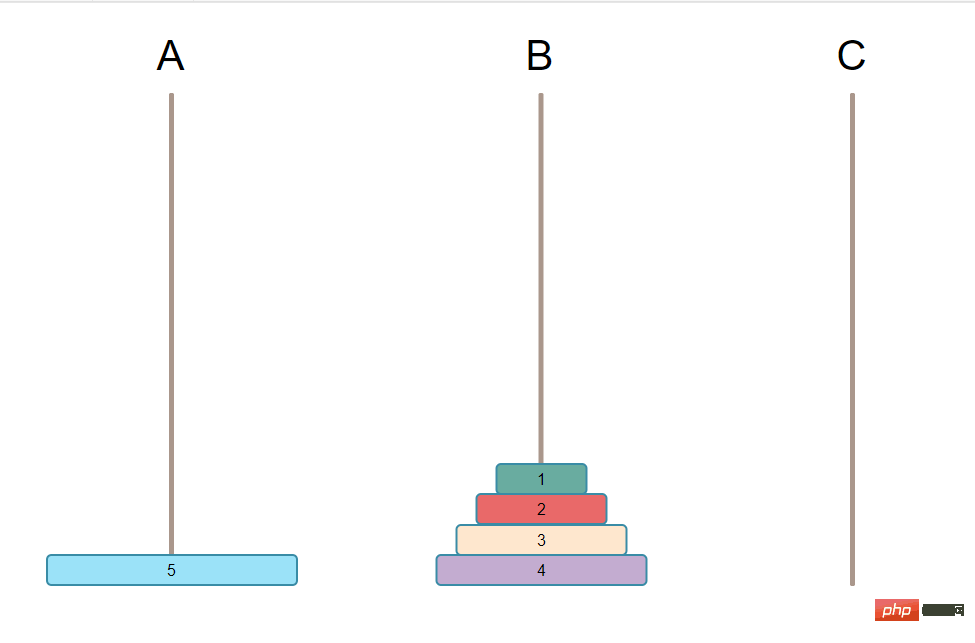🎜🎜Da wir nach C wechseln wollen, müssen wir, um den ersten Schritt zu erreichen, unbedingt alle N-1-Platten in die Säule B verschieben. Nur so kann die N-te Platte (also die größte Platte) Zur Säule C verschieben. 🎜🎜Verschieben Sie N-1-Schilder zur Säule B. Da die Bedingungen erfüllt sein müssen, sind die größeren unten und die kleineren oben, also diese N-1-Schilder befinden sich auf der Säule B. Auch die Säulen sind in Ordnung. 🎜🎜Verschieben Sie diese N-1-Platten schließlich von Säule B zu Säule C, um das Endziel zu erreichen. 🎜🎜🎜Zusammenfassend: 🎜🎜🎜Der erste Schritt besteht darin, N-1-Platten von A nach B zu verschieben. 🎜🎜🎜Warum müssen wir N-1 zuerst nach B verschieben? Sie sehen, weil das, was Sie letztendlich erreichen, darin besteht, alle Platten von A nach C zu verschieben, kann die Reihenfolge nicht geändert werden, es kann nur sein, dass die großen unten und die kleinen oben sind. Dann müssen Sie unbedingt zuerst den größten nach C verschieben, sonst sind die Bedingungen nicht erfüllt. 🎜🎜Um den größten Teller von A nach C zu bewegen, müssen Sie den größten Teller auf A räumen, das heißt, alle Teller auf dem größten Teller müssen bewegt werden. Und Sie haben nur 3 Säulen. Auf C dürfen keine weiteren Plattengriffe vorhanden sein, sonst erfüllen Sie die Bedingungen nicht. Alle diese N-1-Platten können nur auf B platziert werden, und sie sind noch in Ordnung. Es entsteht das folgende Bild: 🎜🎜🎜🎜🎜🎜Der zweite Schritt besteht darin, die N-te Platte auf A (d. h. die größte Platte) nach C zu verschieben. 🎜🎜<p>Das ist ganz einfach. Bewegen Sie einfach die größte Platte in einem Schritt von A nach C. Wie unten gezeigt: </p> <p><img src="https://img.php.cn/upload/article/000/000/020/e50df609a8b176f56d217b586766b982-4.png" alt="Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert"></p> <p><strong>Der dritte Schritt besteht darin, N-1-Platten von B nach C zu verschieben. </strong></p> <p>Hinweis: Um N-1-Platten nach C zu verschieben, müssen Sie die größte Platte unter ihnen finden und dann die größte Platte zuerst verschieben. Hier geht es also tatsächlich darum, die Schritte 1 und 2 zu wiederholen, den größten unter diesen N-1 zu finden und ihn zuerst nach C zu verschieben, und der Zyklus wiederholt sich. </p> <p>Der dritte Schritt entspricht tatsächlich der Änderung der Anforderungen. Angenommen, K = N – 1. <br>Auf Säule B befinden sich K-Schilder, Säule A ist leer und Säule C hat die größte Platte, sodass es bei Säule B mit K-Schildern gleichbedeutend ist, als wäre sie leer. <br>Der erste Schritt besteht darin, die K-1-Platten von B nach A zu verschieben. <br>Der zweite Schritt besteht darin, die K-te Platte von B nach C zu verschieben. <br>Der dritte Schritt besteht darin, die K-1-Platten von A nach C zu verschieben. <br>...</p> <p> wird zum Bild unten</p> <p>Suchen Sie zuerst den größten unter den verbleibenden Tellern</p> <p><img src="https://img.php.cn/upload/article/000/000/020/d1d947b567fd3d8a2295e09c8ff26bf1-5.png" alt=""></p> <p>und verschieben Sie dann den größten Teller</p> <p><img src="https://img.php.cn/upload/article/000/000/020/d1d947b567fd3d8a2295e09c8ff26bf1-6.png" alt=""></p> <p>Dann schleifen Sie, bis nur noch ein Teller übrig ist, und bewegen Sie sich direkt zu C, das Spiel ist vorbei. </p> <h3> <span class="header-link octicon octicon-link"></span>Hilfssäulen</h3> <p>Was sind Hilfssäulen? Angenommen, alle Platten, die Sie verschieben möchten, befinden sich auf A und das Ziel besteht darin, sich nach C zu bewegen. Dann ist B die Hilfssäule von <code>N-1 Platten. Denn sie können hier nur vorübergehend existieren, sonst entsprechen sie nicht den Spielregeln.

Hier müssen Sie zuerst die Hilfspfeiler herausfinden. Denken Sie nicht darüber nach, wie Sie sie umsetzen, sondern klären Sie zunächst nur die Logik.

• Um von A nach B zu gelangen, ist C die Hilfssäule.
• Um von A nach C zu gelangen, ist B die Hilfssäule
Implementierung
• Durch die obige Analyse können wir erkennen, dass es sich tatsächlich um einen sich wiederholenden Vorgang in einem Zyklus handelt, der der Rekursion sehr ähnlich ist, sodass die Rekursion zur Implementierung verwendet werden kann.

Um die Rekursion zu verwenden, sind zwei Bedingungen erforderlich: 1. Finden Sie die Rekursionsformel ein Teller. Wie lautet also die Wiederholungsformel? Basierend auf der obigen logischen Analyse kann es in drei Schritte zerlegt werden.

Der erste Schritt besteht darin, die [N-1] Platten von A nach B zu verschieben

Der zweite Schritt besteht darin, die [N-te] Platte von A nach C zu verschieben




Der dritte Schritt besteht darin, die [N-te] Platte zu verschieben verbleibend] -1 Stück] Die Platte bewegt sich von B nach C

Das Folgende ist der in PHP implementierte Pseudocode:

class HanoiTower
{
    // 计数器
    public $count = 0;
    /**
     * 汉诺塔实现
     * 
     * @param $n 盘子号
     * @param $A 初始柱子
     * @param $B 中转站
     * @param $C 目标柱子
     */
    public function hanoi($n, $A, $B, $C)
    {
        if ($n == 1) {
            // 退出条件 只剩一个盘子的时候直接从A移动到C
            $this->biggestOne($n, $A, $B, $C);
        } else {
            // Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert把 【n-1】 个盘子从A移动到B 此时C为中转站
            $this->hanoi($n - 1, $A, $C, $B);
            // Analysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert把 【第n】 个盘子从A移动到C
            $this->biggestOne($n, $A, $B, $C);
            // 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
            $this->hanoi($n - 1, $B, $A, $C);
        }
    }
    /**
     * 移动最大的盘子
     * 直接从A移动到C
     */
    public function biggestOne($n, $A, $B, $C)
    {
        ++$this->count;
        echo &#39;第&#39;, $this->count, &#39;步 &#39;, &#39;把 &#39;, $n, &#39;从 &#39;, $A, &#39;移动到&#39;, $C, &#39;<br />&#39;;
    }
}
$n = 5;
$hanoiTower = new HanoiTower();
echo &#39;这是一个有 【&#39;, $n, &#39;】 个盘子的汉诺塔：&#39;, &#39;<br />&#39;;
// 调用执行
$hanoiTower->hanoi($n, &#39;A&#39;, &#39;B&#39;, &#39;C&#39;);
echo &#39;总共需要走：【&#39;, $hanoiTower->count, &#39;】 步&#39;;

Die Ergebnisse sind wie folgt:


         

Das obige ist der detaillierte Inhalt vonAnalysieren Sie, wie PHP den interessanten Tower of Hanoi-Algorithmus implementiert. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!