Detaillierte Erklärung, wie PHP dynamische Programmierung nutzt, um die optimale Kombination aus roten Hüllkurven zu erreichen

                                                                                                               

Kürzlich arbeite ich an einer kleinen Anforderung: Bei jeder Bestellung wird der maximale Wert der roten Umschläge bestimmt, die der Benutzer basierend auf der Menge verwenden kann. Wenn sich der Benutzer für die Verwendung roter Umschläge entscheidet, muss dies dem Benutzer bei der Auswahl des optimalen Rots helfen Wählen Sie aus der Liste der verfügbaren roten Umschläge die erforderliche Kombination aus. Der Wert für den roten Umschlag kommt dem maximal verwendbaren Wert für den roten Umschlag am nächsten oder entspricht ihm. Nachdem ich eine Weile darüber nachgedacht habe, ist das nicht das „0-1-Rucksackproblem“? Endlich kann ich den Algorithmus „dynamische Programmierung“, den ich zuvor gelernt habe, in die Praxis umsetzen!

Was ist dynamische Programmierung?

Dynamische Programmierung (Abkürzung für dynamische Programmierung: DP) ist eine Methode, die in der Mathematik, Managementwissenschaft, Informatik, Wirtschaft und Bioinformatik verwendet wird, indem das ursprüngliche Problem in relativ einfache Methoden zerlegt wird, um es zu lösen komplexe Probleme in Form von Teilproblemen.

Dynamische Programmierung eignet sich häufig für Probleme mit überlappenden Teilproblemen und optimalen Unterstruktureigenschaften. Methoden der dynamischen Programmierung benötigen oft viel weniger Zeit als naive Lösungen.

Anwendbare Szenarien für die dynamische Programmierung

Dynamische Programmierung wird im Allgemeinen verwendet, um das Problem zu lösen, die optimale Lösung zu finden. Bei der Lösung des Problems sind mehrere Entscheidungen erforderlich, und jede Entscheidung erzeugt eine Reihe von Zuständen. Anschließend wird mit der nächsten Entscheidung von der optimalen Entscheidung aus fortgefahren, um schließlich das optimale Ergebnis zu finden.

Darüber hinaus weist die dynamische Programmierung auch drei Merkmale auf:

Optimale Unterstruktureigenschaften

Wenn die in der optimalen Lösung des Problems enthaltene Lösung des Unterproblems ebenfalls optimal ist, nennen wir das Problem optimale Unterstruktur Eigenschaften (d. h. Erfüllung des Optimierungsprinzips). Daher können wir die optimale Lösung des Problems aus der optimalen Lösung des Unterproblems ableiten. Es ist auch verständlich, dass der Zustand der späteren Stufe aus dem Zustand der vorherigen Stufe abgeleitet werden kann.

Keine Nachwirkungen

Das heißt, sobald die Lösung für ein Teilproblem festgelegt ist, ändert sich diese nicht mehr und wird nicht durch nachfolgende Lösungen für das größere Problem, in dem es enthalten ist, beeinflusst.

kann einfach so verstanden werden, dass wir uns bei der Ableitung des Zustands der nachfolgenden Stufe nur um den Zustand der vorherigen Stufe kümmern müssen und uns nicht darum kümmern müssen, wie dieser Zustand Schritt für Schritt abgeleitet wird. Die zweite Bedeutung besteht darin, dass der Status einer bestimmten Phase, sobald sie festgelegt ist, von Entscheidungen in nachfolgenden Phasen nicht mehr beeinflusst wird.

Die überlappende Natur von Unterproblemen

Die überlappende Natur von Unterproblemen bedeutet, dass es sich bei der Verwendung eines rekursiven Algorithmus zur Lösung eines Problems von oben nach unten nicht immer um neue Probleme handelt. und einige Unterprobleme werden oft wiederholt

0-1-Rucksackproblem

Die obige Theorie ist relativ abstrakt und einfach nur Unsinn.

Angenommen, es gibt 5 Gegenstände und ihre Gewichte betragen 2, 2, 5, 11, 4. Jetzt gibt es einen Rucksack und das maximale Gewicht, das er tragen kann, beträgt 10 . Bitte wählen Sie die entsprechenden Artikel aus, die in den Rucksack gelegt werden sollen. 2, 2, 5, 11, 4, 现在有一个背包，能承受的最大重量是 10，请选择合适的物品放入背包，那么能组合出的物品最大重量是多少?

不同的物品组合会有多种不同的状态，我们可以使用 f(i, w) 来表示一种状态，其中 i = index 表示第几个物品， w = weight 表示当前的总重量。

整个问题的求解需要经过 『n』 个阶段，每个阶段都需要决策一个物品是否放入背包，决策的结果只有2种 『放入』 或者 『不放入』。在决策完一个物品后，背包中的物品重量会有很多种不同的状态，我们需要把每一层的 重复状态 合并，然后只留下不同的状态。然后基于上一层的状态结果来推导出下一层的状态结果。最终全部物品决策完就可以找到最优的组合解。

第0（其实也就是第一个物品，按照习惯从0开始下标吧）个物品的重量是2，然后开始决策是否放入背包，结果只有2种。如果放入背包那么此时背包的重量就是2，如果不放入背包那么背包的重量就是0.记作 $status[0][0] = true; 和 $status[0][2] = true; 和上面的 f(i, w)

Verschiedene Kombinationen von Artikeln können viele verschiedene Zustände haben /code> Um einen Zustand darzustellen, wobei i = index die Artikelnummer und w = Weight das aktuelle Gesamtgewicht darstellt.

Das gesamte Problem muss in 『n』 Phasen gelöst werden. In jeder Phase muss entschieden werden, ob ein Gegenstand in den Rucksack gesteckt werden soll. Es gibt nur zwei Ergebnisse der Entscheidung: „In den Rucksack stecken“ oder „Nicht in den Rucksack stecken“. es drin". Nachdem wir uns für einen Gegenstand entschieden haben, wird das Gewicht des Gegenstands im Rucksack viele verschiedene Zustände haben. Wir müssen die 🎜wiederholenden Zustände🎜 jeder Schicht zusammenführen und nur die unterschiedlichen Zustände belassen. Anschließend werden die Statusergebnisse der nächsten Schicht basierend auf den Statusergebnissen der vorherigen Schicht abgeleitet. Am Ende kann nach der Entscheidung aller Punkte die optimale Kombinationslösung gefunden werden. 🎜🎜Das Gewicht des 0. Elements (eigentlich das erste Element, beginnen Sie wie gewohnt mit dem Abonnieren bei 0) beträgt 2, und dann beginnen Sie zu entscheiden, ob es in den Rucksack gelegt werden soll, es gibt nur 2 Ergebnisse. Wenn Sie es in den Rucksack stecken, beträgt das Gewicht des Rucksacks zu diesem Zeitpunkt 2. Wenn Sie es nicht in den Rucksack stecken, beträgt das Gewicht des Rucksacks 0. Markiert als $status[0][0 ] = true; und $ status[0][2] = true; Wie f(i, w) oben, stellt die vorherige Ziffer das Element dar und die letzte Ziffer stellt das Gewicht dar. 🎜🎜Das Gewicht des ersten Gegenstands beträgt immer noch 2, und dann beginnen wir, eine Entscheidung darüber zu treffen. Es gibt nur zwei Möglichkeiten zur Entscheidungsfindung: in den Rucksack stecken oder nicht in den Rucksack stecken, aber es gibt viele Zustandskombinationen, da sie auf dem vorherigen Zustand des Rucksacks basieren. Nach Abschluss der Entscheidung zum ersten Punkt wird es 3 Staaten geben (eigentlich 4 Staaten, aber wenn es 1 Duplikat gibt, wird es nicht gezählt. Es wird immer noch als 3 verschiedene Staaten gezählt). 🎜

Wenn die Entscheidung getroffen wird, den aktuellen Gegenstand in den Rucksack zu legen und der 0. Gegenstand nicht in den Rucksack gelegt wird, ist der Status zu diesem Zeitpunkt $status[1][2 + 0] = true; $status[1][2] = true;
Wenn die Entscheidung getroffen wird, den aktuellen Gegenstand in den Rucksack zu legen, wird auch der 0. Gegenstand in den Rucksack gelegt und der Status zu diesem Zeitpunkt is $status[1][2 + 2] = true; Rucksack, und der 0. Gegenstand wird nicht in den Rucksack gelegt, der Status ist zu diesem Zeitpunkt <code>$status[1] [0 + 0] = true => code>;<br>Wenn die Entscheidung getroffen wird, nicht den aktuellen Gegenstand in den Rucksack zu legen, sondern den 0. Gegenstand in den Rucksack zu legen, dann ist der Status <code>$status[1][0 + 2] = true; => $status[1][2] = true;$status[1][2 + 0] = true; => $status[1][2] = true;
如果决策当前物品放入背包,第0个物品也放入背包，此时的状态是 $status[1][2 + 2] = true; => $status[1][4] = true;

如果决策当前物品不放入背包,第0个物品不放入背包，此时的状态是 $status[1][0 + 0] = true; => $status[1][0] = true;
如果决策当前物品不放入背包,而第0个物品放入背包，此时的状态是 $status[1][0 + 2] = true; => $status[1][2] = true;

其中 $status[1][2] 是重复的，所有会产生3种结果。

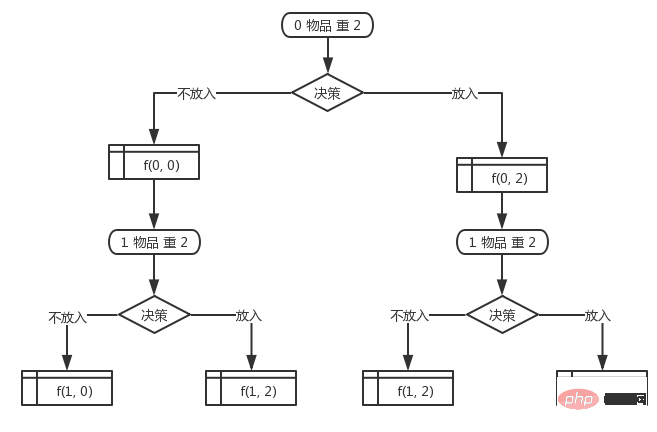
后面的物品也是以此类推，直到对所有的物品都决策完，整个状态的数组就都找出来了，然后只需要在最后一层找到一个值为true的最接近最大值(上面的例子中是10)的值就是背包能承受的最大值。然后可以从最后依次往前推就可以找出对应的物品下标，也就是哪些物品的组合是这个最优解组合了。

推导过程如下图：

实际上在上面的推导过程中就是Detaillierte Erklärung, wie PHP dynamische Programmierung nutzt, um die optimale Kombination aus roten Hüllkurven zu erreichen的解题思路。把问题分解为多个阶段，每个阶段对应一种策略。然后记录下每个阶段的状态（注意要去掉重复项），然后通过当前状态的可能推导出下一个阶段的所有状态可能，动态的推导下去。

PHP实现伪代码：

function dynamicKnapsack($arr, $n, $max){
    // 初始化二维数组
    $status = [];
    for ($i = 0; $i = 0; $j--) {
        if ($status[$n - 1][$j] == true) {
            break;
        }
    }
    for ($i = $n - 1; $i >= 1; $i--) { // 外层遍历行
        if ($j - $arr[$i] >= 0 && $status[$i - 1][$j - $arr[$i]] == 1) {
            var_dump('buy this product: '.$arr[$i]);
            $best[] = $i;
            $j = $j - $arr[$i];
        }
    }
    if ($j != 0) {
        var_dump('buy first product:'.$arr[0]);
        $best[] = 0;
    }
    return $best;}// 测试数据$arr = [
    2, 2, 5, 11, 4,];$n = 5;$max = 10;$best = dynamicKnapsack($arr, $n, $max);var_dump($best);

如果求的结果是 11，得出的结果是 4, 5, 2 的组合，你可能会有疑问不是还有11这个结果么，刚好它一个就满足了不是么。我觉得这个应该是看实际的需求。比如我这次的需求是把红包按过期时间排序，快过期的优先使用，然后我在组装数据的时候按过期时间顺序强行把快过期的红包放到数组最后面拼成数组，那最后的4就是最接近快过期的红包了，我要优先消耗掉这个红包，如果使用了4那11就不能使用了，只能继续去前面找，就是这么回事！

总结

这段代码的时间复杂度是多少? 耗时最多的部分是中间的嵌套2层循环，所有时间复杂度是 O(n*max)，其中 n 表示物品的个数，max表示最大的承重。

空间复杂度是一开始申请的数组空间 O(n*max+1) 加上计算结果的累加有可能出现 O(n*2*max)

wobei $status[1][2 ] wiederholt wird und 3 Ergebnisse liefert.

Die folgenden Elemente sind ebenfalls gleich . , bis alle Elemente entschieden wurden, wurde das gesamte Statusarray gefunden, und dann müssen Sie nur noch einen Wert in der letzten Ebene finden, der dem Maximalwert von true (10 im obigen Beispiel) am nächsten kommt der Wert des Rucksacks. Anschließend können Sie vom Ende aus die entsprechenden Elementindizes herausfinden, d. h. welche Elementkombination die optimale Lösungskombination darstellt. Der Ableitungsprozess ist wie folgt:

Tatsächlich ist der obige Ableitungsprozess Ideen zur Lösung dynamischer Programmierprobleme. Teilen Sie das Problem in Phasen auf, wobei jede Phase einer Strategie entspricht. Zeichnen Sie dann den Status jeder Stufe auf (achten Sie darauf, Duplikate zu entfernen) und leiten Sie dann alle möglichen Zustände der nächsten Stufe aus den Möglichkeiten des aktuellen Zustands ab und leiten Sie diese dynamisch ab.

Pseudocode der PHP-Implementierung: 🎜rrreee🎜Wenn das Ergebnis 11 ist und das Ergebnis eine Kombination aus 4, 5, 2 ist, haben Sie möglicherweise Zweifel auch das Ergebnis von 11, es reicht einfach zufällig aus, nicht wahr? Ich denke, das sollte von den tatsächlichen Bedürfnissen abhängen. Diesmal besteht meine Anforderung beispielsweise darin, die roten Umschläge nach Ablaufzeit zu sortieren und diejenigen zu verwenden, die bald ablaufen. Beim Zusammenstellen der Daten erzwinge ich dann, dass die roten Umschläge, die bald ablaufen, an das Ende des Arrays verschoben werden in der Reihenfolge der Ablaufzeit, um ein Array zu bilden. Dann ist es der rote Umschlag, der bald abläuft. Wenn ich 4 verwende, kann ich nicht 11 verwenden Suchen Sie danach. Das ist es! 🎜

🎜Zusammenfassung

🎜Wie hoch ist die zeitliche Komplexität dieses Codes? Der zeitaufwändigste Teil ist die verschachtelte zweischichtige Schleife in der Mitte , alle Die zeitliche Komplexität beträgt O(n*max), wobei n die Anzahl der Elemente und max die maximale Tragfähigkeit darstellt. 🎜🎜Die Raumkomplexität ist der am Anfang beantragte Array-Raum O(n*max+1) plus die Anhäufung von Berechnungsergebnissen kann O(n*2*max) sein Code > ist der Platzverbrauch immer noch sehr hoch. 🎜🎜 Generell handelt es sich dabei um eine Idee, Raum gegen Zeit zu tauschen. Wenn Sie j verwenden, um in der verschachtelten Schleife der Zwischenentscheidung von klein nach groß zu wechseln, besteht außerdem das Problem wiederholter Berechnungen in der for-Schleife. 🎜🎜🎜Empfohlenes Lernen: „🎜PHP-Video-Tutorial🎜“

Das obige ist der detaillierte Inhalt vonDetaillierte Erklärung, wie PHP dynamische Programmierung nutzt, um die optimale Kombination aus roten Hüllkurven zu erreichen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!