Wie wird die Durchquerung in der richtigen Reihenfolge durchgeführt?

Die Durchquerungsmethode der Reihenfolge-Durchquerung lautet: Durchlaufen Sie für den aktuellen Knoten zuerst den linken Teilbaum, besuchen Sie dann den aktuellen Knoten und durchqueren Sie schließlich den rechten Teilbaum. In-Order-Traversal ist eine Art binärer Baum-Traversal, auch Mid-Root-Traversal und In-Order-Tour genannt.

Die Betriebsumgebung dieses Tutorials: Windows 7-System, C++17-Version, Dell G3-Computer.

Der Binärbaum ist eine wichtige Datenstruktur, und es ist auch wichtig, den Binärbaum zu durchlaufen. Hier stellen wir kurz drei Methoden zum Durchlaufen von Binärbäumen in der richtigen Reihenfolge vor. Beim Durchlaufen eines Binärbaums in der richtigen Reihenfolge wird zunächst der linke Teilbaum durchlaufen, dann der aktuelle Knoten besucht und schließlich der rechte Teilbaum durchlaufen. Für den folgenden Binärbaum lautet das Ergebnis der Durchquerung in der Reihenfolge wie folgt:

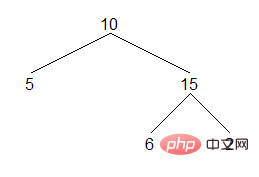
Ergebnis: [5,10,6,15,2]

Intuitiv lautet die Durchquerung des Binärbaums in der Reihenfolge: Projizieren Sie den Knoten auf eine horizontale Koordinatenhöhe. Wie im Bild gezeigt:

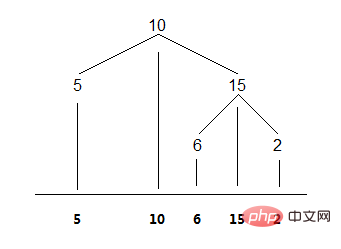
1. Rekursive Methode

Dies ist die einfachste Methode, leicht vorstellbar und leicht zu implementieren. Die Beendigungsbedingung der Rekursion besteht darin, ob der aktuelle Knoten leer ist. Zuerst durchläuft der rekursive Aufruf den linken Teilbaum, besucht dann den aktuellen Knoten und schließlich wird der rechte Teilbaum rekursiv aufgerufen. Der Code lautet wie folgt:

//recursive
class Solution1 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        inorderHelper(ret,root);
        return ret;
    }
private:
    void inorderHelper(vector<int>& ret,TreeNode* root)
    {
        if(root==NULL)return;
        inorderHelper(ret,root->left);
        ret.push_back(root->val);
        inorderHelper(ret,root->right);
    }
};

2. Iterative Methode

Beginnen Sie bei der iterativen Methode mit dem Wurzelknoten, um den Knoten ganz links im Binärbaum zu finden, speichern Sie die übergebenen Knoten in einem Stapel und greifen Sie nach dem Finden auf den Knoten ganz links zu Für jeden Knoten handelt es sich im Allgemeinen um den Wurzelknoten des Teilbaums, der sich selbst als Wurzel darstellt. Nachdem Sie darauf zugegriffen haben, können Sie zum richtigen untergeordneten Knoten wechseln. Der Code lautet wie folgt:

//iterate,using a stack
class Solution2 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        stack<TreeNode*> st;
        while(!st.empty()||curr!=NULL)
        {
            while(curr!=NULL)
            {
                st.push(curr);
                curr=curr->left;
            }
            curr=st.top();
            st.pop();
            ret.push_back(curr->val);
            curr=curr->right;
        }
        return ret;
    }
};

Die zeitliche Komplexität dieser Methode beträgt O(n) und die räumliche Komplexität beträgt ebenfalls O(n).

3. Morris-Methode

Diese Methode wurde von Morris erfunden. Nachdem ich sie gelesen habe, finde ich sie äußerst exquisit. Diese Methode verwendet keine Rekursion, keinen Stapel und schließt die Binärbaumdurchquerung mit der Raumkomplexität O (1) ab. Die Grundidee dieser Methode besteht darin, den rechten Sohn aller Knoten, deren rechter Sohn NULL ist, auf den Nachfolgerknoten zu verweisen (bei Knoten, deren rechter Sohn nicht null ist, ist der rechte Sohn der Knoten, der als nächstes besucht wird). Auf diese Weise zeigt der rechte Sohn jedes Knotens nach dem Zugriff auf ihn auf den nächsten zu besuchenden Knoten. Für den Knoten ganz rechts ist kein solcher Vorgang erforderlich. Beachten Sie, dass dieser Vorgang während des Durchlaufs abgeschlossen wird und der Baum nach Abschluss des Knotenzugriffs wiederhergestellt wird. Die Beurteilungsbedingung der gesamten Schleife besteht darin, ob der aktuelle Knoten leer ist. Im obigen Binärbaum ist der Durchlaufvorgang beispielsweise wie folgt (je nach Position des aktuellen Knotens c):

(1) Der aktuelle Knoten ist 10, da der linke Sohn nicht leer ist und nicht darauf zugegriffen werden kann . Finden Sie den Knoten p ganz rechts im linken Teilbaum von c:

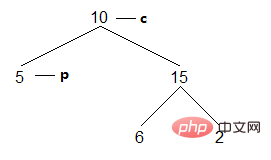
Ergebnis: []

(2) Es gibt zwei Beendigungsbedingungen zum Finden des Knotens ganz rechts im linken Teilbaum von Knoten c Der rechte Sohn ist leer, und der andere ist, dass der rechte Sohn auf den aktuellen Knoten zeigt. Das Folgende ist der Fall, in dem der rechte Sohn leer ist. Dieser Fall muss zuerst konstruiert werden, indem der rechte Sohn des Knotens p auf den Nachfolgerknoten c gerichtet wird und dann c nach unten verschoben wird:

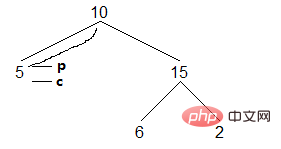
Ergebnis: []

(3) Aktueller Knoten c Der linke Sohn ist leer und es wird darauf zugegriffen. Zeigen Sie nach dem Zugriff mit c auf den rechten Sohn (d. h. den Nachfolgerknoten):

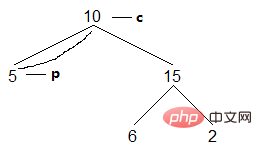
Ergebnis: [5]

(4) Suchen Sie weiter nach dem Knoten ganz rechts im linken Teilbaum. Diesmal nach der Beendigungsbedingung ist, dass der Knoten ganz rechts der aktuelle Knoten ist. Dies zeigt, dass der linke Teilbaum des aktuellen Knotens durchlaufen wurde. Stellen Sie nach dem Besuch des aktuellen Knotens den Binärbaum wieder her und verweisen Sie den aktuellen Knoten auf den Nachfolgerknoten:

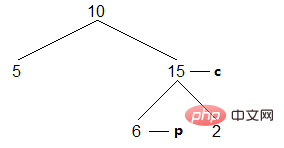
Ergebnis: [5,10]

( 5) Wiederholen Sie den obigen Vorgang, bis c auf den Knoten ganz rechts im gesamten Binärbaum zeigt:

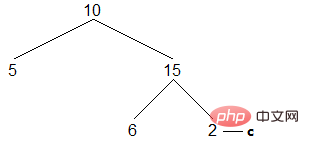
Der linke Sohn ist leer, der Zugriff wird ausgeführt und c geht zum rechten Sohn. Der rechte Sohn ist leer und erfüllt die Beurteilungsbedingung nicht. Die Schleife endet und der Durchlauf ist abgeschlossen. Das Ergebnis ist wie folgt:

[5,10,6,15,2]

Dies ist die Morris-Methode, die Zeitkomplexität ist O(n) und die Raumkomplexität ist O(1). Der Code lautet wie folgt:

//Morris traversal,without a stack
class Solution3 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        TreeNode *pre;
        while(curr)
        {
            if(curr->left==NULL)
            {
                ret.push_back(curr->val);
                curr=curr->right;
            }
            else
            {
                pre=curr->left;
                while(pre->right&&pre->right!=curr)
                    pre=pre->right;
                if(pre->right==NULL)
                {
                    pre->right=curr;
                    curr=curr->left;
                }
                else
                {
                    ret.push_back(curr->val);
                    pre->right=NULL;
                    curr=curr->right;
                }
            }
        }
        return ret;
    }
};

Empfohlenes Tutorial: „C#“

Das obige ist der detaillierte Inhalt vonWie wird die Durchquerung in der richtigen Reihenfolge durchgeführt?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!