Heim >Backend-Entwicklung >PHP-Problem >So implementieren Sie die Fakultät von n in PHP
So implementieren Sie die Fakultät von n in PHP
- 藏色散人Original
- 2021-06-03 09:16:185260Durchsuche
So implementieren Sie die Fakultät von n in PHP: 1. Implementieren Sie sie durch gewöhnliche Rekursion mit Code wie „function fact(int $n): int{...}“; 2. Implementieren Sie sie mit gewöhnlichen Schleifen mit Code wie „while ($num

Die Betriebsumgebung dieses Artikels: Windows 10-System, PHP-Version 7.2.15, DELL G3-Computer
Wie implementiert man die Fakultät von n in PHP?
Soweit ich weiß, ist die Implementierung Fakultätsmethoden können im Allgemeinen in drei Typen unterteilt werden. Im üblichen Sinne werden Rekursion und Schleife jeweils als ein Typ betrachtet, und es gibt auch eine große Kategorie, die einige clevere mathematische Methoden verwendet, um die Anzahl der Operationen (insbesondere die Anzahl der Multiplikationen) zu reduzieren Operationen) und optimiert so die Berechnungseffizienz.
Wenn Sie die Fakultät hochpräziser, großer Ganzzahlen berücksichtigen möchten, wird die Situation für die PHP-Sprache komplizierter. Wenn Sie beispielsweise einige von der BCMath-Erweiterung bereitgestellte Methoden verwenden, sind explizite Zahlen- und Zeichenfolgenkonvertierungsoperationen häufiger .
In diesem Artikel wird versucht, die oben genannten Situationen zu implementieren, wenn n nur als ganze Zahl betrachtet wird. In jedem Fall werden verfügbare Codebeispiele angegeben, und am Ende des Artikels ist ein umfassender Vergleich mehrerer Methoden angehängt.
Gewöhnliche rekursive Implementierung
Die erste ist die gewöhnliche rekursive Implementierung. Gemäß der allgemeinen Formel der Rekursion fact(n) = n * fact(n-1) ist es einfach, den Fakultätsberechnungscode zu schreiben. Der Vorteil einer gewöhnlichen rekursiven Implementierung besteht darin, dass der Code relativ prägnant ist und der gleiche Prozess wie bei der allgemeinen Formel das Verständnis des Codes erleichtert. Der Nachteil besteht darin, dass aufgrund der häufigen Selbstaufrufe eine große Anzahl von Push- und Pop-Vorgängen erforderlich ist und die Gesamtberechnungseffizienz nicht hoch ist (siehe Tabelle am Ende des Artikels).
function fact(int $n): int
{
if ($n == 0) {
return 1;
}
return $n * fact($n - 1);
}Gewöhnliche Schleifenimplementierung
Gewöhnliche Schleifenimplementierung hat ein bisschen den Geschmack einer „dynamischen Programmierung“, aber da die Zwischenzustandsvariablen seltener verwendet werden und keinen zusätzlichen Speicherplatz erfordern, sind sie einfacher als gewöhnliche dynamische Programmieralgorithmen . Die gewöhnliche rekursive Methode ist ein Berechnungsprozess von oben nach unten (von n bis 1), während die gewöhnliche Schleife eine Berechnung von unten nach oben ist.
Relativ gesehen ist der Code also nicht so intuitiv wie die obige Methode, aber da es weniger häufige Push- und Pop-Prozesse gibt, ist die Berechnungseffizienz höher (siehe Tabelle am Ende des Artikels).
function fact(int $n): int
{
$result = 1;
$num = 1;
while ($num <= $n) {
$result = $result * $num;
$num = $num + 1;
}
return $result;
}Selbst implementierte große ganzzahlige Fakultät
Aufgrund der Bereichsbeschränkung des int-Typs in PHP können die beiden oben genannten Methoden nur Fakultäten bis zu 20 genau berechnen. Wenn Sie nur die Fakultät von 20 berücksichtigen, ist es schneller, die Nachschlagetabellenmethode zu verwenden: Berechnen Sie die Fakultät von 0-20 im Voraus, speichern Sie sie in einem Array und fragen Sie sie bei Bedarf einmal ab.
Um sich an die Fakultät großer Zahlen anpassen zu können und genaue Berechnungsergebnisse zu erhalten, wurde dieser Artikel basierend auf der „normalen Schleifenmethode“ verbessert, bei der jedes Bit im Berechnungsergebnis (von niedrig nach hoch) in einem Array gespeichert wird ) und nacheinander multiplizieren und übertragen. Berechnen Sie das Ergebnis für jede Ziffer.
Es versteht sich von selbst, dass der Vorteil dieser Methode darin besteht, dass sie auf hochpräzise Situationen mit großen Fakultäten angewendet werden kann. Der Nachteil besteht darin, dass der Berechnungsprozess für kleine Fakultäten kompliziert und langsam ist.
function fact(int $n): array
{
$result = [1];
$num = 1;
while ($num <= $n) {
$carry = 0;
for ($index = 0; $index < count($result); $index++) {
$tmp = $result[$index] * $num + $carry;
$result[$index] = $tmp % 10;
$carry = floor($tmp / 10);
}
while ($carry > 0) {
$result[] = $carry % 10;
$carry = floor($carry / 10);
}
$num = $num + 1;
}
return $result;
}BCMath-Erweiterungsmethode
BCMath ist eine mathematische Erweiterung für PHP, die numerische Berechnungen für durch Zeichenfolgen dargestellte Zahlen (beliebiger Größe und Genauigkeit) verarbeitet. Da es sich um eine in der C-Sprache implementierte Erweiterung handelt, ist die Berechnungsgeschwindigkeit schneller als bei der oben genannten Selbstimplementierung.
Empfohlenes Lernen: „PHP-Video-Tutorial“
Auf meinem Laptop berechne ich auch die Fakultät von 2000. Die Selbstimplementierung dauert durchschnittlich 0,5–0,6 Sekunden und die Verwendung von BCMath dauert 0,18–0,19 Sekunden. Der Hauptnachteil dieser Methode besteht darin, dass die Installation entsprechender Erweiterungen erforderlich ist. Bei Anwendungen, bei denen Upgrades des Umweltmanagements unpraktisch sind, ist die Praktikabilität fraglich.
function fact(int $n): string
{
$result = '1';
$num = '1';
while ($num <= $n) {
$result = bcmul($result, $num);
$num = bcadd($num, '1');
}
return $result;
}Optimierungsalgorithmus
Wie am Anfang dieses Artikels erwähnt, versucht der Optimierungsalgorithmus, die Anzahl der Operationen (insbesondere die Anzahl der Multiplikationsoperationen) so weit wie möglich zu reduzieren, um eine schnelle Fakultät zu erreichen. Wenn man bedenkt, dass für kleine ganzzahlige Fakultäten der schnellste Algorithmus die Tabellensuchmethode mit einer Zeitkomplexität von O(1) sein sollte, wird in diesem Abschnitt hauptsächlich die exakte Fakultät großer ganzer Zahlen besprochen und getestet.
Es versteht sich, dass die faktorielle Optimierung derzeit häufiger durch die Formel n! = C(n, n/2) * (n/2)! durchgeführt wird Formel Das Highlight ist hauptsächlich die Optimierung von C(n, n/2). In Anbetracht der Tatsache, dass bei großen Ganzzahlen die Effizienz der PHP-Sprache zur Implementierung von C (n, n/2) nicht hoch ist und die Lesbarkeit des Codes relativ schlecht ist (häufige explizite Konvertierung von Zahlen und Zeichenfolgen), wird in diesem Artikel verwendet Eine weitere cleverere Methode.
Die Berechnungsgeschwindigkeit der Multiplikation ist normalerweise geringer als die der Addition und Subtraktion. Durch die Reduzierung der Anzahl der Multiplikationsoperationen kann die Gesamtberechnungsgeschwindigkeit verbessert werden. Durch mathematische Induktion können wir herausfinden, dass wir für die Fakultät von n nacheinander Werte finden können, die 1, 1+3, 1+3+5 ... kleiner als (n/2)^2 sind, und diese dann multiplizieren können führen Sie sie der Reihe nach aus, um den Zielwert zu erhalten.
Der Vorteil dieses Algorithmus besteht darin, dass die Berechnungsgeschwindigkeit schnell ist. Der Nachteil besteht jedoch darin, dass der Implementierungsprozess nicht intuitiv und leicht zu verstehen ist. Nach dem Test berechnet der folgende Code die faktorielle Durchschnittszeit von 2000 auf 0,11 Sekunden, was etwa der Hälfte der Zeit der normalen Schleifenmethode entspricht.
Zusätzlich zu dieser Optimierungsmethode haben wir auch andere ähnliche Ideen gesehen, z. B. die wiederholte Überprüfung, ob die Zahlen in 1 ... n durch 2 teilbar sind, das Aufzeichnen der Anzahl der Teilbarkeiten durch 2 x und den Versuch, sie zusammenzufassen Gemeinsame ungerade Zahlen Multiplizieren Sie die Formel und multiplizieren Sie sie schließlich mit 2^x, um das Ergebnis zu erhalten.
function fact(int $n): string
{
$middleSquare = pow(floor($n / 2), 2);
$result = $n & 1 == 1 ? 2 * $middleSquare * $n : 2 * $middleSquare;
$result = (string)$result;
for ($num = 1; $num < $n - 2; $num = $num + 2) {
$middleSquare = $middleSquare - $num;
$result = bcmul($result, (string)$middleSquare);
}
return $result;
}综合对比
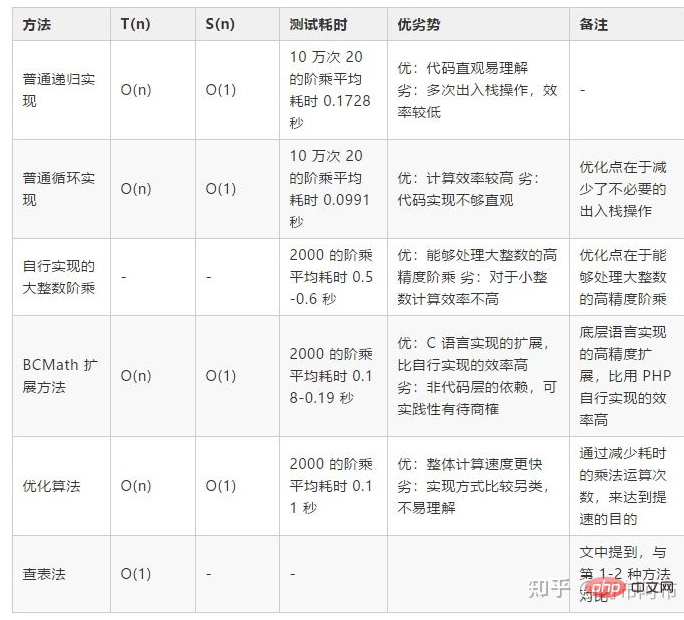
本文中提到的方法是按照由劣到优的顺序,因此,下列表格中每一行中提到优劣势,主要是和其上一两种方法对比。
表格中「测试耗时」一列的测试环境为个人笔记本,硬件配置为 Dell/i5-8250U/16GB RAM/256GB SSD Disk,软件配置为 Win 10/PHP 7.2.15。
总结
虽然本文将实现方法分为三大类,但其实也可以分为循环和递归两大类,在这两类中分别使用相应的算法优化计算效率。But,总体而言,循环的效率要优于递归。
讲道理,本文中使用的优化算法并不是最优解,只是用 PHP 相对好实现,代码易读性也比较高。有兴趣的读者可以谷歌了解更多的骚操作。
Das obige ist der detaillierte Inhalt vonSo implementieren Sie die Fakultät von n in PHP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

