Ausführliche Erklärung zur Implementierung der Warteschlangenstruktur in JavaScript

In diesem Artikel erfahren Sie mehr über die Datenstruktur der Warteschlange, stellen deren Vorgänge im Detail vor und erfahren, wie Sie die Warteschlangenstruktur in JavaScript implementieren. Es hat einen gewissen Referenzwert. Freunde in Not können sich darauf beziehen. Ich hoffe, es wird für alle hilfreich sein.

1. Warteschlangendatenstruktur

Warteschlange ist eine Art „First In, First Out“-Datenstruktur (FIFO). Das erste in die Warteschlange eingereihte Element (Eingabe) ist das erste aus der Warteschlange entfernte Element (Ausgabe).

Die Warteschlange hat 2 Zeiger: Kopf und Schwanz. Das älteste in der Warteschlange befindliche Element befindet sich am Anfang und das neueste in der Warteschlange befindliche Element am Ende.

Die Warteschlange ist so, als würden wir in der U-Bahn anstehen. Passagiere in der Nähe der Tür stehen an der Spitze der Warteschlange, und Passagiere, die gerade in die Warteschlange eingetreten sind, stehen am Ende der Warteschlange.

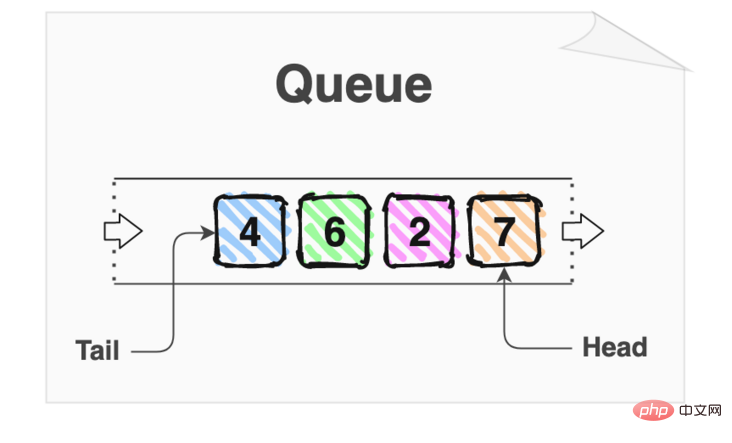
Aus einer höheren Perspektive ist eine Warteschlange eine Datenstruktur, die es uns ermöglicht, jedes Datenelement der Reihe nach in der Reihenfolge zu verarbeiten, in der es gespeichert ist.

2. Warteschlangenoperationen

Die Warteschlange unterstützt zwei Hauptoperationen: enqueue(enqueue) und dequeue(dequeue), zusätzlich zu Peek- und Längenoperationen.

2.1 Enqueue-Vorgang

Der Enqueue-Vorgang fügt ein Element am Ende der Warteschlange ein und macht es so zum Ende der Warteschlange.

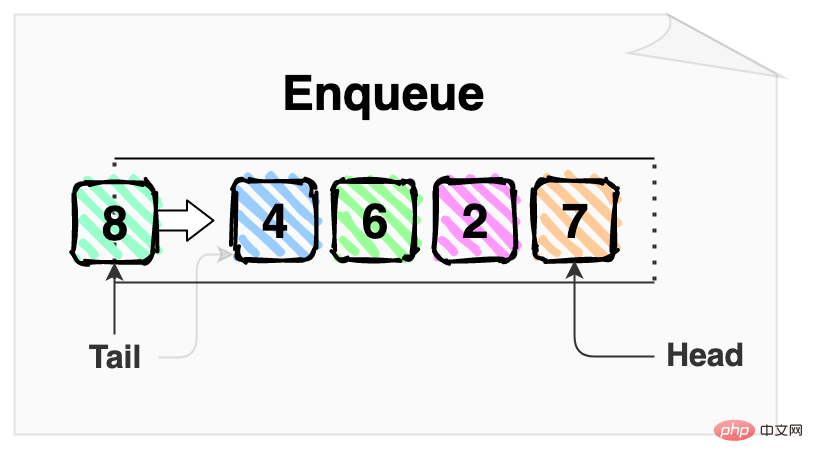
Der Verbindungsvorgang im obigen Bild fügt 8 am Ende der Warteschlange ein, und dann wird 8 zum Ende der Warteschlange. 8，之后 8 成为队列的队尾。

queue.enqueue(8);

2.2 出队操作

出队操作取出队列中第一个项目，此时队列中的下一个项目成为队首。

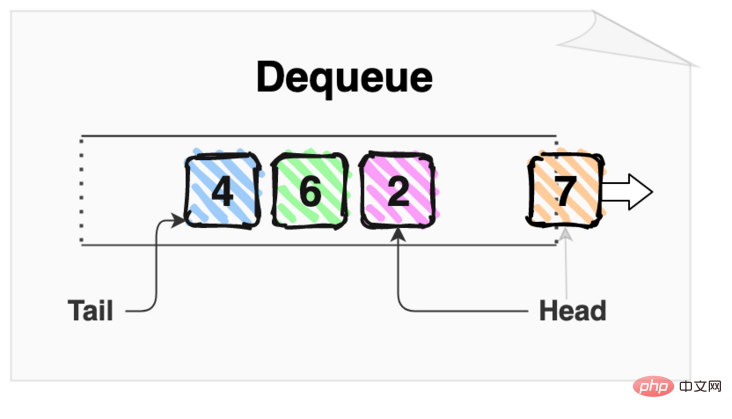
在上图中，出队操作返回项目7并从队列中删除。 出队之后之后，项目 2 成为新的队首。

queue.dequeue(); // => 7

2.3 Peek 操作

Peek 操作读取队首的项目，但是不改变队列。

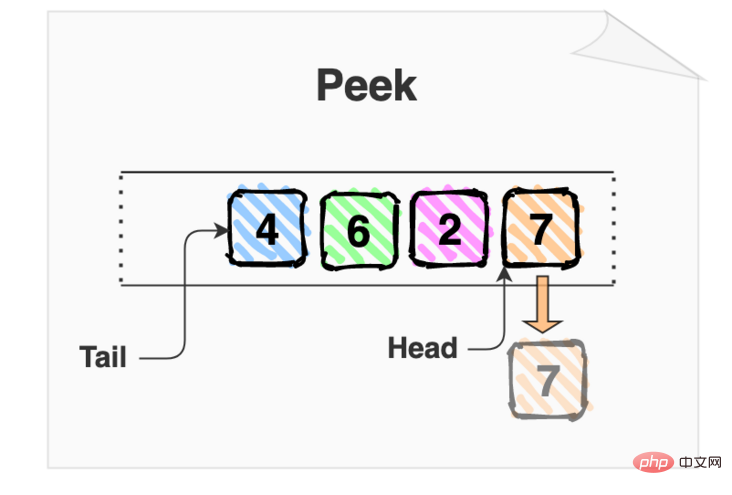
上图中  7 是队首。 peek 操作只需返回队首 7 但是不修改队列。

queue.peek(); // => 7

2.4 length

length 操作返回队列中包含项目的数量。

上图中的队列有 4 项：4、6、2 和。7。结果队列长度为 4。

queue.length; // => 4

2.5 队列操作的时间复杂度

关于队列所有操作的重点：enqueue，dequeue，peek 和 length 必须以常数时间复杂度 O(1) 执行。

常数时间复杂度 O(1) 意味着无论队列大小如何（不管是有 10 个还是 100 万个项目），这些操作都必须在相对一致的时间内执行。

3. 用 JavaScript 实现队列

来看一下怎样在保证所有操作必须以常数时间复杂度O(1) 要求实现队列这种数据结构。

class Queue {
  constructor() {
    this.items = {};
    this.headIndex = 0;
    this.tailIndex = 0;
  }

  enqueue(item) {
    this.items[this.tailIndex] = item;
    this.tailIndex++;
  }

  dequeue() {
    const item = this.items[this.headIndex];
    delete this.items[this.headIndex];
    this.headIndex++;
    return item;
  }

  peek() {
    return this.items[this.headIndex];
  }

  get length() {
    return this.tailIndex - this.headIndex;
  }
}

const queue = new Queue();

queue.enqueue(7);
queue.enqueue(2);
queue.enqueue(6);
queue.enqueue(4);

queue.dequeue(); // => 7

queue.peek();    // => 2

queue.length;    // => 3

const queue = new Queue() 是创建队列的实例。

queue.enqueue(7) 方法将 7 存入队列中。

queue.dequeue() 从队列中取出一个头部项目，而 queue.peek() 只读队首项。

最后的 Queue.Length 显示队列中还有多少个项目。

关于实现：在 Queue 类中，普通对象  this.Items  将队列的项目通过数值索引保持。 队首项的索引由 Where.HeadInex 跟踪，队尾项由 this.tailIndex 跟踪。

队列方法的复杂度

在 Queue 的 queue()、 dequeue()、 peek() 和 length() 方法中存在：

• 属性访问器（如:this.items[this.headIndex]），
• 执行算数操作（如:this.headidex++）

这些方法的时间复杂度是恒定的时间 O(1)。

4. 总结

队列是一种遵循先入先出（FIFO）规则的的数据结构。

队列有 2 个主要操作：入队和出队。 另外，队列可以有辅助操作，例如 peek 和 length。

所有队列操作都必须以常数时间 O(1) 执行。

挑战一下：改进 dequeue() 和 peek()rrreee

2.2 Vorgang zum Entfernen aus der Warteschlange

Der Vorgang zum Entfernen aus der Warteschlange entfernt das erste Element in der Warteschlange und das nächste Element in der Warteschlange wird zum Anführer der Warteschlange.

🎜🎜🎜at In der obigen Abbildung gibt der Vorgang zum Entfernen aus der Warteschlange das Element 7 zurück und löscht es aus der Warteschlange. Nachdem Gegenstand 2 aus der Warteschlange entfernt wurde, wird er zum neuen Teamleiter. 🎜rrreee🎜🎜2.3 Peek-Operation 🎜🎜🎜Die Peek-Operation liest das Element an der Spitze der Warteschlange, ändert jedoch nicht die Warteschlange. 🎜🎜🎜🎜Up Im Bild ist 7 der Anführer des Teams. Die Peek-Operation gibt lediglich den Kopf der Warteschlange 7 zurück, verändert die Warteschlange jedoch nicht. 🎜rrreee🎜🎜2.4 Länge🎜🎜🎜Die Längenoperation gibt die Anzahl der in der Warteschlange enthaltenen Elemente zurück. 🎜🎜🎜🎜Up Die Warteschlange im Bild besteht aus 4 Elementen: 4, 6, 2 und . 7. Die resultierende Warteschlangenlänge beträgt 4. 🎜rrreee🎜🎜2.5 Zeitkomplexität von Warteschlangenoperationen 🎜🎜🎜 Wichtige Punkte zu allen Operationen an Warteschlangen: Enqueue, Dequeue, Peek und Länge müssen mit konstanter Zeitkomplexität O(1) ausgeführt werden. 🎜🎜Konstante Zeitkomplexität O(1) bedeutet, dass diese Vorgänge unabhängig von der Warteschlangengröße (ob 10 oder 1 Million Elemente) in relativ konstanter Zeit ausgeführt werden müssen. 🎜🎜🎜3. Verwenden Sie JavaScript, um Warteschlangen zu implementieren. 🎜🎜🎜 Werfen wir einen Blick darauf, wie die Warteschlangendatenstruktur implementiert wird und gleichzeitig sichergestellt wird, dass alle Operationen mit konstanter Zeitkomplexität O(1) ausgeführt werden müssen. 🎜rrreee🎜const queue = new Queue() ist eine Instanz, die eine Warteschlange erstellt. 🎜🎜Die Methode queue.enqueue(7) speichert 7 in der Warteschlange. 🎜🎜queue.dequeue() entfernt ein Kopfelement aus der Warteschlange, während queue.peek() nur das Kopfelement der Warteschlange liest. 🎜🎜Der letzte Queue.Length zeigt an, wie viele Elemente noch in der Warteschlange sind. 🎜🎜Über die Implementierung: In der Klasse Queue speichert das gewöhnliche Objekt this.Items die Elemente der Warteschlange über numerische Indizes. Der Index des ersten Elements in der Warteschlange wird von Where.HeadInex verfolgt, und der Index des letzten Elements in der Warteschlange wird von this.tailIndex verfolgt. 🎜

🎜Die Komplexität der Warteschlangenmethode🎜

🎜In Queues queue(), dequeue(), Es gibt die Methoden peek() und length(): 🎜

• Eigenschafts-Accessoren (z. B.: this.items[this.headIndex] code >),
• Arithmetische Operationen ausführen (z. B.: this.headidex++)

🎜Die zeitliche Komplexität dieser Methoden ist eine konstante Zeit O (1). 🎜🎜🎜4. Zusammenfassung🎜🎜🎜Warteschlange ist eine Datenstruktur, die der First-In-First-Out-Regel (FIFO) folgt. 🎜🎜Queue hat zwei Hauptoperationen: Einreihen und Entfernen aus der Warteschlange. Darüber hinaus können Warteschlangen über Hilfsoperationen wie Peek und Länge verfügen. 🎜🎜Alle Warteschlangenoperationen müssen in konstanter Zeit O(1) ausgeführt werden. 🎜🎜🎜Herausforderung: Verbessern Sie die Methoden dequeue() und peek(), um einen Fehler auszulösen, wenn sie in einer leeren Warteschlange ausgeführt werden. 🎜🎜🎜Weitere Kenntnisse zum Thema Programmierung finden Sie unter: 🎜Einführung in die Programmierung🎜! ! 🎜

Das obige ist der detaillierte Inhalt vonAusführliche Erklärung zur Implementierung der Warteschlangenstruktur in JavaScript. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!