Heim >häufiges Problem >Was ist der Zweck der Datennormalisierung?
Was ist der Zweck der Datennormalisierung?
- 青灯夜游Original
- 2021-05-07 16:33:1828020Durchsuche
Der Zweck der Datennormalisierung besteht darin, die vorverarbeiteten Daten auf einen bestimmten Bereich zu beschränken und so die durch einzelne Beispieldaten verursachten nachteiligen Auswirkungen zu beseitigen. Nach der Datennormalisierung kann die Geschwindigkeit des Gradientenabstiegs zum Finden der optimalen Lösung beschleunigt und die Genauigkeit verbessert werden (z. B. KNN).

Die Betriebsumgebung dieses Tutorials: Windows 7-System, Dell G3-Computer.
Im Bereich des maschinellen Lernens werden verschiedene Bewertungsindikatoren verwendet (das heißt, unterschiedliche Merkmale im Merkmalsvektor sind die unterschiedlichen Bewertungsindikatoren) Diese Situation wirkt sich häufig auf die Ergebnisse der Datenanalyse aus. Um den dimensionalen Einfluss zwischen Indikatoren zu beseitigen, ist eine Datenstandardisierung erforderlich, um das Problem der Vergleichbarkeit zu lösen . Nachdem die Originaldaten durch Datenstandardisierung verarbeitet wurden, liegt jeder Indikator in derselben Größenordnung, was für eine umfassende vergleichende Bewertung geeignet ist. Unter diesen ist die Normalisierungsverarbeitung von Daten die typischste. (Sie können sich auf die Studie beziehen: Datenstandardisierung/-normalisierung ) Kurz gesagt besteht der Zweck der Normalisierung darin, die vorverarbeiteten Daten auf einen bestimmten Bereich zu beschränken (z. B. [0,1 ] oder [-1,1]), wodurch die nachteiligen Auswirkungen beseitigt werden, die durch
singuläre Beispieldatenverursacht werden. 1) In der Statistik besteht die spezifische Rolle der Normalisierung darin, die statistische Verteilung einer einheitlichen Stichprobe zusammenzufassen. Die Normalisierung zwischen 0 und 1 ist eine statistische Wahrscheinlichkeitsverteilung und die Normalisierung zwischen -1 und +1 ist eine statistische Koordinatenverteilung.
2) Singuläre Beispieldaten beziehen sich auf Beispielvektoren (d. h. Merkmalsvektoren), die im Vergleich zu anderen Eingabebeispielen besonders groß oder klein sind. Im Folgenden sind Beispieldaten x1 und x2 mit zwei Merkmalen aufgeführt , x3, x4, x5, x6 (Merkmalsvektor -> Spaltenvektor), wobei sich die beiden Merkmale der x6-Stichprobe relativ von anderen Stichproben unterscheiden. Daher wird x6 als singuläre Stichprobendaten betrachtet.
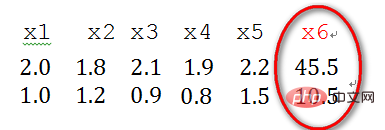
Das Vorhandensein einzelner Beispieldaten führt zu einer Verlängerung der Trainingszeit und kann auch dazu führen, dass die Konvergenz fehlschlägt. Vor dem Training müssen die vorverarbeiteten Daten normalisiert werden. Wenn hingegen keine einzelnen Beispieldaten vorhanden sind, muss keine Normalisierung durchgeführt werden.
--Wenn keine Normalisierung durchgeführt wird, wird die Zielfunktion aufgrund des großen Unterschieds in den Werten verschiedener Features im Feature „flach“. Vektor. Auf diese Weise weicht die Richtung des Gradienten beim Durchführen eines Gradientenabstiegs von der Richtung des Minimalwerts ab und erfordert viele Umwege, was bedeutet, dass die Trainingszeit zu lang wird.
– Bei Normalisierung erscheint die Zielfunktion „runder“, was das Training erheblich beschleunigt und viele Umwege vermeidet. Zusammenfassend hat die Normalisierung folgende Vorteile, nämlich 1) Nach der Normalisierung wird der Gradientenabstieg beschleunigt optimale Lösung; 2) Normalisierung kann die Genauigkeit verbessern (wie KNN) Hinweis: Es gibt keine standardisierten Datenmethoden, die angewendet werden für jedes Problem und jedes Modell kann die Genauigkeit des Algorithmus verbessern und die Konvergenzgeschwindigkeit des Algorithmus beschleunigen. Weitere Informationen zu diesem Thema finden Sie in der Rubrik „FAQ“! 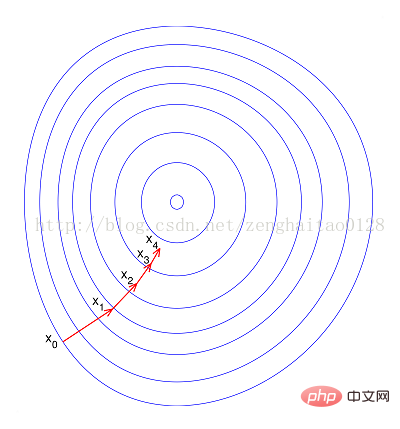
Das obige ist der detaillierte Inhalt vonWas ist der Zweck der Datennormalisierung?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Python-Methode zur Normalisierung mehrdimensionaler Arrays
- Wie läuft beim Datenbankdesign die Konvertierung eines ER-Diagramms in ein relationales Datenmodell ab?
- Was ist der Unterschied zwischen Datenbankansichten und Tabellen?
- So erhalten Sie den letzten Wert einer Datenspalte in Excel
- Welchen Zweck hat die Erstellung von Indizes für Datentabellen in der Phase des physischen Datenbankentwurfs?

