Front-End-Interview: Implementierung von 6 klassischen Sortieralgorithmen, wie viele kennen Sie? (Angehängte Animation + Video)

In diesem Artikel werden die Implementierungsmethoden von 6 klassischen Sortieralgorithmen erläutert und mit Ihnen geteilt. Es hat einen gewissen Referenzwert. Freunde in Not können sich darauf beziehen. Ich hoffe, es wird für alle hilfreich sein.

Der Sortieralgorithmus ist ein hochfrequenter Inspektionspunkt in Vorstellungsgesprächen, und wir müssen ihn beherrschen. In diesem Artikel wurden die klassischsten und am häufigsten verwendeten Sortieralgorithmen zusammengestellt und mit Animationen und Videos kombiniert, um Ihnen dabei zu helfen, sie leichter zu gewinnen.

Erstens kann der Sortieralgorithmus entsprechend den Eigenschaften in die folgenden zwei Kategorien unterteilt werden:

• Vergleichende Sortierung
• Nicht vergleichende Sortierung

Wie der Name schon sagt, Vergleichende Sortierung ist Sortierung durch Vergleich zwischen Elementen. Nicht-Vergleichsklassen beinhalten keine Vergleichsoperationen zwischen Elementen. 比较类排序是通过元素间的比较进行排序的，非比较类则不涉及元素之间的比较操作。

比较类排序的时间复杂度不能突破 O(nlogn)，也被称为非线性排序。

非比较类排序的时间复杂度可以突破 O(nlogn)，能够以线性的时间运行，也被称为线性排序。

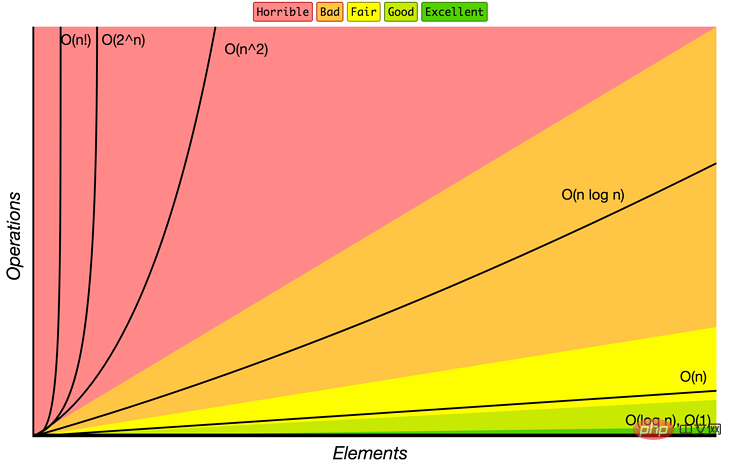
如果你还不了解时间复杂度的话，可以移步我的这篇专栏JavaScript算法时间、空间复杂度分析。

01 冒泡排序 Bubble Sort

冒泡排序可视化视频：

https://www.reddit.com/r/programming/comments/e55j0i/bubble_sort_visualization/

冒泡排序，简单粗暴，一句话解释:

冒泡排序在每次冒泡操作时会比较相邻的两个元素，看是否满足大小关系要求，不满足就将它俩互换。一直迭代到不再需要交换，也就是排序完成。

const bubbleSort = function(arr) {
  const len = arr.length
  if (len < 2) return arr
  for (let i = 0; i < len; i++) {
      for (let j = 0; j < len - i - 1; j++) {
          if (arr[j] > arr[j + 1]) {
              const temp = arr[j]
              arr[j] = arr[j + 1]
              arr[j + 1] = temp
          }
      }
  }
  return arr
}

• 时间复杂度: O(n^2)
• 空间复杂度: O(1)
• 稳定

注意：这里的稳定是指，冒泡排序是稳定的排序算法。

什么是稳定的排序算法呢？

排序算法的稳定性

仅仅用执行效率和内存消耗来判断排序算法的优劣是不够的，针对排序算法，还有一个重要的度量指标，稳定性。

意思是说，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

举个：

比如我们有一组数据：1，9，2，5，8，9。按照大小排序之后就是 1，2，5，8，9，9。

这组数据中有两个 9，经过某种排序算法排序后，如果两个 9 的前后顺序没有改变，我们就把这种排序算法称为 稳定的排序算法。
否则，就是不稳定的排序算法。

冒泡排序优化

上面的代码还可以进行优化，当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不需要再继续执行后续的冒泡操作了。

const bubbleSort = function(arr) {
  const len = arr.length
  let flag = false
  if (len < 2) return arr
  for (let i = 0; i < len; i++) {
      flag = false // 提前退出冒泡循环的标志
      for (let j = 0; j < len - i - 1; j++) {
          if (arr[j] > arr[j + 1]) {
              const temp = arr[j]
              arr[j] = arr[j + 1]
              arr[j + 1] = temp
              flag = true // 表示有数据交换
          }
      }
      if (!flag) break // 没有数据交换，提前退出
  }
  return arr
}

02 插入排序 Insertion Sort

插入排序顾名思义，对于未排序的数据，在已排序的序列中从后往前扫描，找到相应的位置进行插入，保持已排序序列中元素一直有序。

从 i 等于 1 开始遍历，拿到当前元素 curr，与前面的元素进行比较。

如果前面的元素大于当前元素，就把前面的元素和当前元素进行交换，不断循环直到未排序序列中元素为空，排序完成。

const insertSort = function(arr) {
    const len = arr.length
    let curr, prev
    for (let i = 1; i < len; i++) {
        curr = arr[i]
        prev = i - 1
        while (prev >= 0 && arr[prev] > curr) {
            arr[prev + 1] = arr[prev]
            prev--
        }
        arr[prev + 1] = curr
    }
    return arr
}

• 时间复杂度: O(n^2)
• 空间复杂度: O(1)
• 稳定

03 选择排序 Selection Sort

选择排序可视化视频：

https://www.reddit.com/r/programming/comments/e5md13/selection_sort_visualization/

选择排序和插入排序有些类似，也分已排序序列和未排序序列。

但是选择排序是将最小的元素存放在数组起始位置，再从剩下的未排序的序列中寻找最小的元素，然后将其放到已排序的序列后面。以此类推，直到排序完成。

const selectSort = function(arr) {
    const len = arr.length
    let temp, minIndex
    for (let i = 0; i < len - 1; i++) {
        minIndex = i
        for (let j = i + 1; j < len; j++) {
            if (arr[j] <= arr[minIndex]) {
                minIndex = j
            }
        }
        temp = arr[i]
        arr[i] = arr[minIndex]
        arr[minIndex] = temp
    }
    return arr
}

• 时间复杂度: O(n^2)
• 空间复杂度: O(1)
• 不稳定

04 归并排序 Merge Sort

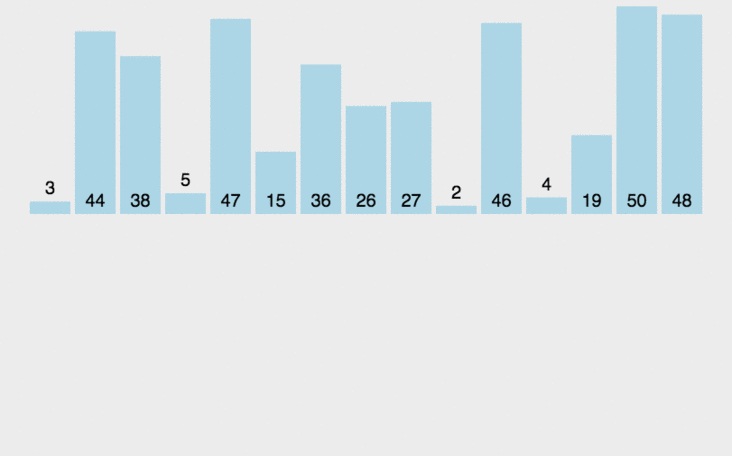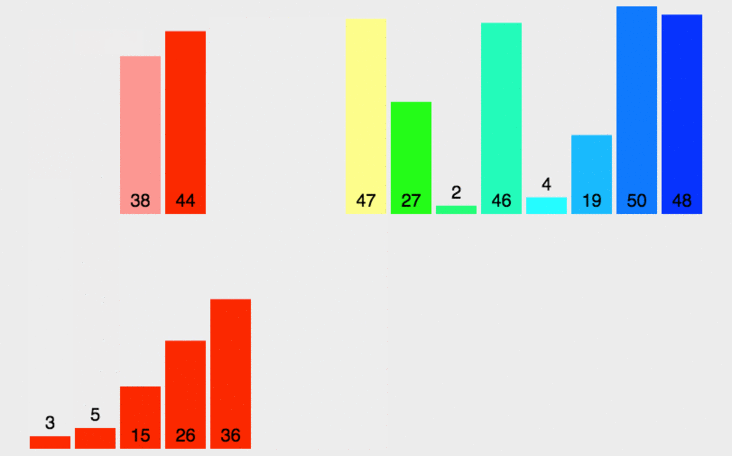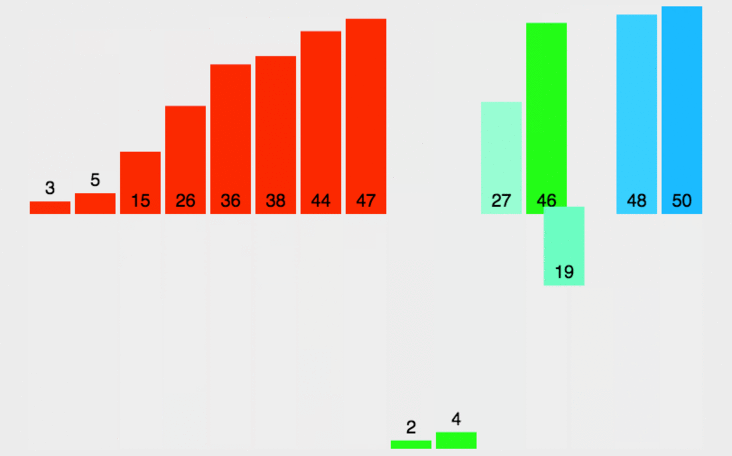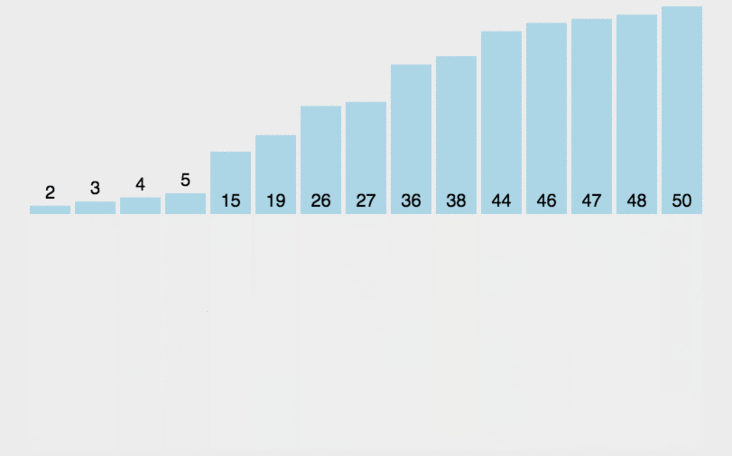
分治法典型应用，分治算法思想很大程度上是基于递归的，也比较适合用递归来实现。

处理过程是由下到上的，先处理子问题，然后再合并。

Die zeitliche Komplexität der Vergleichssortierung darf O(nlogn) nicht überschreiten, was auch als nichtlineare Sortierung bezeichnet wird. 🎜🎜Die zeitliche Komplexität der Sortierung ohne Vergleich kann O(nlogn) überschreiten und in linearer Zeit ausgeführt werden, auch bekannt als lineare Sortierung. 🎜🎜🎜🎜Wenn Sie die Zeitkomplexität noch nicht verstehen, können Sie zu meiner Spalte „Analyse der Zeit- und Raumkomplexität des JavaScript-Algorithmus“ wechseln. 🎜

01 Blasensortierung

🎜Video zur Visualisierung der Blasensortierung: 🎜🎜https://www.reddit.com/r/programming/comments/e55j0i /bubble_sort_visualization/🎜

🎜Blasensortierung, einfach und grob, Erklärung in einem Satz:🎜🎜Blasensortierung vergleicht bei jedem Blasenvorgang zwei benachbarte Elemente, um zu sehen, ob die Größenbeziehungsanforderungen erfüllt sind, wenn nicht, sie werden ausgetauscht. Wiederholen Sie den Vorgang, bis kein Austausch mehr erforderlich ist, d. h. die Sortierung ist abgeschlossen. 🎜

const mergeSort = function(arr) {
    const merge = (right, left) => {
    const result = []
    let i = 0, j = 0
    while (i < left.length && j < right.length) {
      if (left[i] < right[j]) {
        result.push(left[i++])
      } else {
        result.push(right[j++])
      }
    }
    while (i < left.length) {
      result.push(left[i++])
    }
    while (j < right.length) {
      result.push(right[j++])
    }
    return result
    }
    const sort = (arr) => {
        if (arr.length === 1) { return arr }
        const mid = Math.floor(arr.length / 2)
        const left = arr.slice(0, mid)
        const right = arr.slice(mid, arr.length)
        return merge(mergeSort(left), mergeSort(right))
    }
    return sort(arr)
}

🎜🎜Zeitkomplexität: O(n^2)🎜🎜Raumkomplexität: O(1)🎜🎜Stabil🎜🎜🎜Hinweis: „Stabil“ bedeutet hier, dass die Blasensortierung ein stabiler Sortieralgorithmus ist. 🎜🎜Was ist ein stabiler Sortieralgorithmus? 🎜

Stabilität des Sortieralgorithmus

🎜Nur Ausführungseffizienz und Speicherverbrauch verwenden, um die Qualität des Sortieralgorithmus zu beurteilen . Wenn das nicht reicht, gibt es noch eine weitere wichtige Metrik für Sortieralgorithmen: stabilität. 🎜🎜Das bedeutet, dass sich die ursprüngliche Reihenfolge zwischen den gleichen Elementen nach dem Sortieren nicht ändert, wenn in der zu sortierenden Sequenz Elemente mit gleichen Werten vorhanden sind. 🎜🎜Zum Beispiel: 🎜

Zum Beispiel haben wir einen Datensatz: 1, 9, 2, 5, 8, 9. Nach der Sortierung nach Größe sind es 1, 2, 5, 8, 9, 9.

🎜Es gibt zwei Neunen in diesem Datensatz. Wenn sich die Reihenfolge der beiden Neunen nach der Sortierung nach einem bestimmten Sortieralgorithmus nicht ändert, nennen wir diesen Sortieralgorithmus einen stabilen Sortieralgorithmus code> . 🎜Ansonsten handelt es sich um einen <code>instabilen Sortieralgorithmus. 🎜

Optimierung der Blasensortierung

🎜Der obige Code kann auch optimiert werden, wenn für eine bestimmte Blasenoperation kein Datenaustausch erfolgt Vollständig geordnet, keine Notwendigkeit, weitere Sprudelvorgänge durchzuführen. 🎜

const quickSort = function(arr) {
    const quick = function(arr) {
        if (arr.length <= 1) return arr
        const len = arr.length
        const index = Math.floor(len >> 1)
        const pivot = arr.splice(index, 1)[0]
        const left = []
        const right = []
        for (let i = 0; i < len; i++) {
            if (arr[i] > pivot) {
                right.push(arr[i])
            } else if (arr[i] <= pivot) {
                left.push(arr[i])
            }
        }
        return quick(left).concat([pivot], quick(right))
    }
    const result = quick(arr)
    return result
}

02 Einfügungssortierung

🎜🎜🎜Wie der Name schon sagt, für unsortierte Daten, in der sortierten Reihenfolge, von Vorwärts scannen und suchen die entsprechende Position zum Einfügen, wobei die Elemente in der sortierten Reihenfolge in der richtigen Reihenfolge bleiben. 🎜🎜Beginnen Sie mit der Durchquerung von i gleich 1, ermitteln Sie den aktuellen Elementstrom und vergleichen Sie ihn mit dem vorherigen Element. 🎜🎜Wenn das vorherige Element größer als das aktuelle Element ist, tauschen Sie das vorherige Element mit dem aktuellen Element aus und fahren Sie mit der Schleife fort, bis das Element in der unsortierten Sequenz leer ist und die Sortierung abgeschlossen ist. 🎜

const heapSort = function(arr) {
    buildHeap(arr, arr.length - 1)
    let heapSize = arr.length - 1 // 初始化堆的有效序列长度
    for (let i = arr.length - 1; i > 1; i--) {
        swap(arr, 1, i) // 交换堆顶元素与最后一个有效子元素
        heapSize-- // 有效序列长度减 1
        heapify(arr, heapSize, 1) // 堆化有效序列
    }
    return arr
}

// 构建大顶堆
const buildHeap = function(items, heapSize) {
    // 从后往前并不是从序列的最后一个元素开始，而是从最后一个非叶子节点开始，这是因为，叶子节点没有子节点，不需要自上而下式堆化。
    // 最后一个子节点的父节点为 n/2 ，所以从 n/2 位置节点开始堆化
    for (let i = Math.floor(heapSize / 2); i >= 1; i--) {
        heapify(items, heapSize, i)
    }
}
// 堆化
const heapify = function(arr, heapSize, i) {
    while (true) {
        let maxIndex = i
        if (2 * i <= heapSize && arr[i] < arr[i * 2]) {
            maxIndex = i * 2
        }
        if (2 * i + 1 <= heapSize && arr[maxIndex] < arr[i * 2 + 1]) {
            maxIndex = i * 2 + 1
        }
        if (maxIndex === i) break
        swap(arr, i, maxIndex)
        i = maxIndex
    }
}

// 交换工具函数
const swap = function(arr, i, j) {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

🎜🎜Zeitkomplexität: O(n^2)🎜🎜Raumkomplexität: O(1)🎜🎜Stabil🎜🎜

03 Auswahlsortierung

🎜Auswahlsortierung Visualisierungsvideo: 🎜🎜https://www.reddit.com/r/programming/comments/e5md13/selection_sort_visualization/🎜

🎜Auswahlsortierung und Einfügungssortierung sind etwas ähnlich und werden auch in sortierte und unsortierte Sequenzen unterteilt Sequenzen Reihenfolge sortieren. 🎜🎜Aber die Auswahlsortierung besteht darin, das kleinste Element am Anfang des Arrays zu speichern, dann das kleinste Element aus der verbleibenden unsortierten Sequenz zu finden und es dann nach der sortierten Sequenz einzufügen. Und so weiter, bis die Sortierung abgeschlossen ist. 🎜rrreee🎜🎜Zeitkomplexität: O(n^2)🎜🎜Raumkomplexität: O(1)🎜🎜Unstabil🎜🎜

04 Merge Sort

🎜 🎜🎜Eine typische Anwendung des Divide-and-Conquer-Algorithmus. Die Idee des Divide-and-Conquer-Algorithmus basiert weitgehend auf Rekursion und eignet sich besser für die Implementierung mithilfe von Rekursion. 🎜🎜Der Bearbeitungsprozess erfolgt von unten nach oben, wobei zunächst Teilprobleme behandelt und dann zusammengeführt werden. 🎜

如果感觉自己对递归掌握的还不是很透彻的同学，可以移步我的这篇专栏你真的懂递归吗？。

顾名思义，分而治之。一般分为以下三个过程：

• 分解：将原问题分解成一系列子问题。

• 解决：递归求解各个子问题，若子问题足够小，则直接求解。

• 合并：将子问题的结果合并成原问题。

归并排序就是将待排序数组不断二分为规模更小的子问题处理，再将处理好的子问题合并起来，这样整个数组就都有序了。

const mergeSort = function(arr) {
    const merge = (right, left) => {
    const result = []
    let i = 0, j = 0
    while (i < left.length && j < right.length) {
      if (left[i] < right[j]) {
        result.push(left[i++])
      } else {
        result.push(right[j++])
      }
    }
    while (i < left.length) {
      result.push(left[i++])
    }
    while (j < right.length) {
      result.push(right[j++])
    }
    return result
    }
    const sort = (arr) => {
        if (arr.length === 1) { return arr }
        const mid = Math.floor(arr.length / 2)
        const left = arr.slice(0, mid)
        const right = arr.slice(mid, arr.length)
        return merge(mergeSort(left), mergeSort(right))
    }
    return sort(arr)
}

• 时间复杂度: O(nlogn)
• 空间复杂度: O(n)
• 稳定

05 快速排序 Quick Sort

快速排序可视化视频：

https://www.reddit.com/r/dataisbeautiful/comments/e9fb2k/oc_quicksort_visualization/

快速排序也是分治法的应用，处理过程是由上到下的，先分区，然后再处理子问题。

快速排序通过遍历数组，将待排序元素分隔成独立的两部分，一部分记录的元素均比另一部分的元素小，则可以分别对这两部分记录的元素继续进行排序，直到排序完成。

这就需要从数组中挑选出一个元素作为 基准(pivot)，然后重新排序数列，将元素比基准值小的放到基准前面，比基准值大的放到基准后面。

然后将小于基准值的子数组(left)和大于基准值的子数组(right)递归地调用 quick 方法，直到排序完成。

const quickSort = function(arr) {
    const quick = function(arr) {
        if (arr.length <= 1) return arr
        const len = arr.length
        const index = Math.floor(len >> 1)
        const pivot = arr.splice(index, 1)[0]
        const left = []
        const right = []
        for (let i = 0; i < len; i++) {
            if (arr[i] > pivot) {
                right.push(arr[i])
            } else if (arr[i] <= pivot) {
                left.push(arr[i])
            }
        }
        return quick(left).concat([pivot], quick(right))
    }
    const result = quick(arr)
    return result
}

• 时间复杂度: O(nlogn)
• 空间复杂度: O(nlogn)
• 不稳定

06 堆排序 Heap Sort

堆排序相比其他几种排序代码会有些复杂，不过没关系，我们先来看一些前置知识，可以帮助我们更好的理解堆排序。

堆排序顾名思义就是要利用堆这种数据结构进行排序。堆是一种特殊的树，满足以下两点就是堆：

• 堆是一个完全二叉树

• 堆中每一个节点的值都必须大于等于(或小于等于)其子树中的每个节点的值

每个节点的值都大于等于子树中每个节点值的堆，叫做大顶堆，每个节点的值都小于等于子树中每个节点值的堆，叫做小顶堆。

也就是说，大顶堆中，根节点是堆中最大的元素。小顶堆中，根节点是堆中最小的元素。

如果你对树这种数据结构还不是很了解，可以移步我的这篇专栏“树”业有专攻

堆如果用一个数组表示的话，给定一个节点的下标 i (i从1开始)，那么它的父节点一定为 A[i / 2]，左子节点为 A[2i]，右子节点为 A[2i + 1]。

堆排序包含两个过程，建堆和排序。首先构建一个大顶堆，也就是将最大值存储在根节点(i = 1)，每次取大顶堆的根节点与堆的最后一个节点进行交换，此时最大值放入了有效序列的最后一位，并且有效序列减 1，有效堆依然保持完全二叉树的结构，然后进行堆化成为新的大顶堆。重复此操作，直到有效堆的长度为 0，排序完成。

const heapSort = function(arr) {
    buildHeap(arr, arr.length - 1)
    let heapSize = arr.length - 1 // 初始化堆的有效序列长度
    for (let i = arr.length - 1; i > 1; i--) {
        swap(arr, 1, i) // 交换堆顶元素与最后一个有效子元素
        heapSize-- // 有效序列长度减 1
        heapify(arr, heapSize, 1) // 堆化有效序列
    }
    return arr
}

// 构建大顶堆
const buildHeap = function(items, heapSize) {
    // 从后往前并不是从序列的最后一个元素开始，而是从最后一个非叶子节点开始，这是因为，叶子节点没有子节点，不需要自上而下式堆化。
    // 最后一个子节点的父节点为 n/2 ，所以从 n/2 位置节点开始堆化
    for (let i = Math.floor(heapSize / 2); i >= 1; i--) {
        heapify(items, heapSize, i)
    }
}
// 堆化
const heapify = function(arr, heapSize, i) {
    while (true) {
        let maxIndex = i
        if (2 * i <= heapSize && arr[i] < arr[i * 2]) {
            maxIndex = i * 2
        }
        if (2 * i + 1 <= heapSize && arr[maxIndex] < arr[i * 2 + 1]) {
            maxIndex = i * 2 + 1
        }
        if (maxIndex === i) break
        swap(arr, i, maxIndex)
        i = maxIndex
    }
}

// 交换工具函数
const swap = function(arr, i, j) {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

• 时间复杂度: O(nlogn)
• 空间复杂度: O(1)
• 不稳定

为了方便你理解和记忆，我将这 6 种排序算法的复杂度和稳定性汇总成表格如下：

本文讲解了十大经典排序算法中的 6 种排序算法，这 6 种排序算法是平时开发中比较常见的，大家务必要熟练掌握。

更多编程相关知识，请访问：编程视频！！

Das obige ist der detaillierte Inhalt vonFront-End-Interview: Implementierung von 6 klassischen Sortieralgorithmen, wie viele kennen Sie? (Angehängte Animation + Video). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!