Was ist der Unterschied zwischen knn und k-means?

Der Unterschied zwischen knn und k-means: 1. Der [k-means]-Algorithmus ist ein typischer distanzbasierter Clustering-Algorithmus. Er verwendet den Abstand als Bewertungsindex für die Ähnlichkeit, d. h. es wird davon ausgegangen, dass der Abstand zwischen ihnen geringer ist Je größer die Ähnlichkeit zwischen zwei Objekten, desto größer. Der knn-Algorithmus hat keinen offensichtlichen Vortrainingsprozess. Wenn das Programm gestartet wird, wird der Datensatz in den Speicher geladen und die Klassifizierung beginnt.

Der Unterschied zwischen knn und k-means:

1. Prozess und Prinzip des k-means-Clustering-Algorithmus

k-means-Clustering-Algorithmus ist ein grundlegender A-Partitionierungsalgorithmus mit einer bekannten Anzahl von Clusterkategorien. Es handelt sich um einen typischen abstandsbasierten Clustering-Algorithmus, der den Abstand als Ähnlichkeitsbewertungsindex verwendet. Das heißt, es wird davon ausgegangen, dass die Ähnlichkeit umso größer ist, je geringer der Abstand zwischen zwei Objekten ist. Sie wird mithilfe der euklidischen Distanz gemessen (ein einfaches Verständnis ist die geradlinige Distanz zwischen zwei Punkten. Die euklidische Distanz standardisiert lediglich die Definition dieser Distanz und erweitert sie auf N Dimensionen). Es kann große Datenmengen verarbeiten und ist effizient. Das Clustering-Ergebnis sind k Datensätze, die in k Kategorien unterteilt sind. Entsprechend der Ausdrucksmethode der Clusterergebnisse kann sie in einen Hard-K-Means-Algorithmus (H CM), einen Fuzzy-K-Means-Algorithmus (F CM) und einen Wahrscheinlichkeits-K-Means-Algorithmus (P CM) unterteilt werden.

1.1. Grundidee: Der Algorithmus verwendet eine iterative Aktualisierungsmethode, um das endgültige Clustering-Ergebnis zu erreichen das Maximum Kleiner Wert, um einen besseren Klassifizierungseffekt zu erzielen

1.2 Prinzip

Der ursprüngliche k-means-Algorithmus wählt zunächst zufällig k Punkte als anfängliches Clusterzentrum aus, berechnet dann den Abstand von jedem Datenobjekt zu jedem Clusterzentrum und klassifiziert die Datenobjekte Gehen Sie zu der Klasse, deren Clusterzentrum am nächsten liegt. Berechnen Sie das neue Clusterzentrum für die angepasste neue Klasse. Wenn sich in den beiden benachbarten Clusterzentren keine Änderung ergibt, bedeutet dies, dass die Datenobjektanpassung abgeschlossen ist und die Clustering-Kriteriumsfunktion erfüllt ist f war Konvergenz. Bei jeder Iteration muss überprüft werden, ob die Klassifizierung jeder Stichprobe korrekt ist. Wenn sie nicht korrekt ist, muss sie angepasst werden. Nachdem alle Daten angepasst wurden, wird das Clusterzentrum geändert und die nächste Iteration eingegeben. Wenn alle Datenobjekte in einem iterativen Algorithmus korrekt klassifiziert sind, erfolgt keine Anpassung und keine Änderung im Clusterzentrum, was darauf hinweist, dass f konvergiert hat und der Algorithmus endet.

1.3 Algorithmus-Flussdiagramm

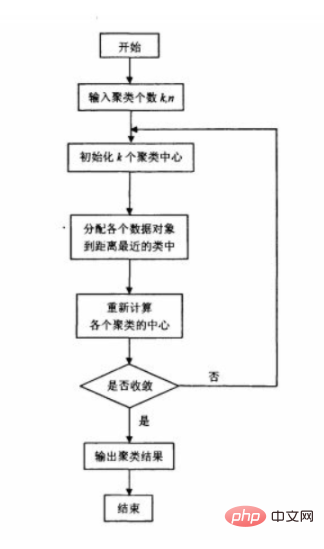1.4 Wie wähle ich den Anfangspunkt des Algorithmus aus?

1) Wählen Sie K Punkte aus, die im Stapel so weit wie möglich voneinander entfernt sind.

Wählen Sie zunächst zufällig einen Punkt als ersten anfänglichen Cluster-Mittelpunkt aus und wählen Sie dann den Punkt, der am weitesten von diesem Punkt entfernt ist, als zweiten anfänglichen Cluster-Mittelpunkt aus. Wählen Sie dann den Punkt mit dem geringsten Abstand zu den ersten beiden Punkten als Mittelpunkt des dritten Anfangsclusters aus, und so weiter, bis K Anfangsclustermittelpunkte ausgewählt sind.

2) Wählen Sie hierarchisches Clustering oder Canopy-Algorithmus für das anfängliche Clustering und verwenden Sie dann die Mittelpunkte dieser Cluster als anfängliche Cluster-Mittelpunkte des K-Means-Algorithmus.

Wie wählt man k im Algorithmus 1.5 aus?

Solange die von uns angenommene Anzahl der Cluster gleich oder höher als die tatsächliche Anzahl der Cluster ist, steigt der Indikator langsam an, und sobald wir versuchen, weniger als die tatsächliche Anzahl der Cluster zu erreichen, steigt der Indikator stark an. Der Clusterindex dient als wichtiger Referenzindex.

Der Durchmesser eines Clusters bezieht sich auf den maximalen Abstand zwischen zwei beliebigen Punkten im Cluster.

Der Radius eines Clusters bezieht sich auf die maximale Entfernung von allen Punkten im Cluster zum Zentrum des Clusters.

1.6 Vorteile, Nachteile und Verbesserungsmöglichkeiten?

Es ist einfach zu verwenden, da es ein zufälliges Element verwendet, sodass nicht garantiert wird, dass die beste Klasse gefunden wird. Es ist keine vernünftige Initialisierung der Anzahl der Cluster erforderlich: Das heißt, K muss initialisiert werden.

2. K-Nearest-Neighbor-Klassifizierungsalgorithmus (K N N)

2.1 Das Problem führt die Idee von

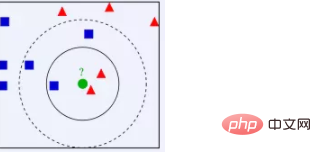K N N ein: Aus der obigen Abbildung können wir ersehen, dass der Datensatz in der Abbildung gut ist Daten, also alle Nach der Beschriftung ist eine Kategorie ein blaues Quadrat, die andere ein rotes Dreieck und der grüne Kreis sind die Daten, die wir klassifizieren möchten. Wenn K=3, dann gibt es 2 rote Dreiecke und 1 blaues Quadrat, die dem grünen Punkt am nächsten liegen, sodass der zu klassifizierende grüne Punkt zum roten Dreieck gehört und 1 blaues Quadrat, das dem grünen Punkt am nächsten liegt. Es gibt 2 rote Dreiecke und 3 blaue Quadrate, sodass der zu klassifizierende grüne Punkt zum blauen Quadrat gehört Benachbarte Proben im MerkmalsraumDie meisten von ihnen gehören zu einer bestimmten Kategorie, dann gehört die Probe auch zu dieser Kategorie. Wir können sehen, dass KNN im Wesentlichen auf einer statistischen Methode basiert! Tatsächlich basieren viele Algorithmen des maschinellen Lernens auch auf Datenstatistiken.

2.2 K N N-Algorithmus

Einführung

K N N steht für K-Nearest Neighbor, eine Art gedächtnisbasiertes Lernen, auch instanzbasiertes Lernen genannt, und gehört zum Lazy Learning. Das heißt, es gibt keinen offensichtlichen Vortrainingsprozess. Wenn das Programm ausgeführt wird, ist nach dem Laden des Datensatzes in den Speicher kein Training erforderlich und die Klassifizierung kann gestartet werden. K N N ist ebenfalls ein überwachter Lernalgorithmus. Er berechnet den Abstand zwischen den Merkmalswerten der neuen Daten und den Trainingsdaten und wählt dann K (K>=1) nächste Nachbarn zur Klassifizierung (Abstimmungsmethode) oder Regression aus. Wenn K=1, werden neue Daten einfach der Klasse ihres nächsten Nachbarn zugewiesen.

Schritte

1) Berechnen Sie den Abstand zwischen den Testdaten und den einzelnen Trainingsdaten. Zur Berechnung können Sie die euklidische Distanzformel verwenden.

2) Sortieren Sie nach zunehmendem Abstandsverhältnis;

3) Wählen Sie die K-Punkte mit dem kleinsten Abstand aus (der k-Wert wird von Ihnen selbst bestimmt)

4) Bestimmen Sie die Häufigkeit des Auftretens der Kategorie des oberen K Punkte;

5) Geben Sie die Kategorie mit der höchsten Häufigkeit unter den ersten K Punkten als vorhergesagte Klassifizierung der Testdaten zurück.

Merkmale

Nichtparametrische statistische Methode: Die Auswahl des Parameters K muss nicht eingeführt werden: Wenn K = 1, wird die zu klassifizierende Probe in die Klasse der Probe klassifiziert, die ihr am nächsten kommt. Wenn K = | K muss vernünftig gewählt werden. Wenn es zu klein ist, wird es leicht gestört, und wenn es zu groß ist, erhöht es die Rechenkomplexität. Die Komplexität des Algorithmus: Der Fluch der Dimensionalität nimmt im Allgemeinen stark zu.

2.3 Vor- und Nachteile des Algorithmus

Vorteile: Einfach und effektiv

Nachteile: Großer Rechenaufwand. Die Ausgabe ist nicht sehr interpretierbar. Alle Trainingsbeispiele müssen gespeichert werden.

3. Der Unterschied zwischen K N N und k-means

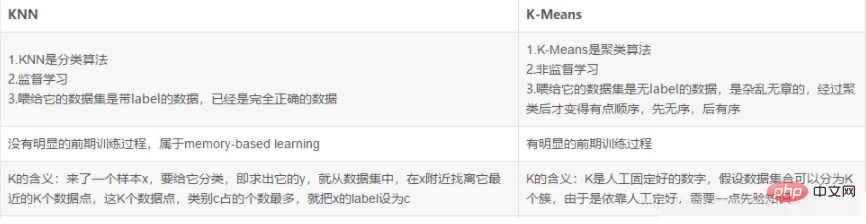
Verwandte kostenlose Lernempfehlungen: php-Programmierung (Video)

Das obige ist der detaillierte Inhalt vonWas ist der Unterschied zwischen knn und k-means?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!