Heim >häufiges Problem >Ein bestimmter Binärbaum hat 5 Knoten mit Grad 2. Wie viele Blattknoten hat dieser Binärbaum?
Ein bestimmter Binärbaum hat 5 Knoten mit Grad 2. Wie viele Blattknoten hat dieser Binärbaum?
- 青灯夜游Original
- 2020-04-22 15:11:3917397Durchsuche
In der Informatik ist ein Binärbaum eine Baumstruktur mit höchstens zwei Teilbäumen pro Knoten. Normalerweise werden Teilbäume als „linker Teilbaum“ und „rechter Teilbaum“ bezeichnet. Binärbäume werden häufig zur Implementierung binärer Suchbäume und binärer Heaps verwendet.

Ein Binärbaum mit der Tiefe k und 2^k-1 Knoten wird als vollständiger Binärbaum bezeichnet. Das Merkmal dieser Art von Baum ist, dass die Anzahl der Knoten auf jeder Ebene der maximalen Anzahl von Knoten entspricht. Wenn in einem Binärbaum mit Ausnahme der letzten Ebene alle anderen Ebenen voll sind und entweder die letzte Ebene voll ist oder rechts mehrere aufeinanderfolgende Knoten fehlen, ist der Binärbaum ein vollständiger Binärbaum. Die Tiefe eines vollständigen Binärbaums mit n Knoten beträgt floor(log2n)+1. Ein vollständiger Binärbaum mit Tiefe k hat mindestens 2k-1 Blattknoten und höchstens 2k-1 Knoten.
Ein bestimmter Binärbaum hat 5 Knoten mit Grad 2. Wie viele Blattknoten hat dieser Binärbaum?
Die Beziehung zwischen der Anzahl der Blattknoten in einem Binärbaum und der Anzahl der Knoten mit Grad 2 ist: Anzahl der Knoten mit Grad 2 = Anzahl der Blattknoten - 1;
Also, die Anzahl der Blattknoten =Die Anzahl der Knoten mit Grad 2+1=6.Erweiterung:
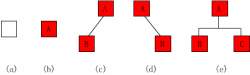
Binärbäume werden rekursiv definiert und ihre Knoten sind in linke und rechte Teilbäume unterteilt. Logischerweise haben Binärbäume fünf Grundformen:- Leerer Binärbaum – wie in (a) gezeigt;
- Ein Binärbaum mit nur einem Wurzelknoten – wie in (b) gezeigt;
- Nur der rechte Teilbaum – wie in (d) gezeigt;
- Vollständiger Binärbaum – Abbildung (e).
 Hinweis: Obwohl Binärbäume viele Ähnlichkeiten mit Bäumen haben, sind Binärbäume kein Sonderfall von Bäumen.
Hinweis: Obwohl Binärbäume viele Ähnlichkeiten mit Bäumen haben, sind Binärbäume kein Sonderfall von Bäumen.
Typ
(1) Vollständiger Binärbaum – Wenn die Höhe des Binärbaums h ist, mit Ausnahme der h-ten Schicht, beträgt die Anzahl der Knoten in allen anderen Schichten (1~h -1) erreicht das Maximum. Es gibt Blattknoten in der h-ten Schicht und die Blattknoten sind von links nach rechts angeordnet. Dies ist ein vollständiger Binärbaum.
(2) Vollständiger Binärbaum – ein Binärbaum, in dem jeder Knoten außer den Blattknoten linke und rechte Unterblätter hat und die Blattknoten alle unten liegen.
(3) Ausgeglichener Binärbaum – Ein ausgeglichener Binärbaum wird auch AVL-Baum genannt (im Gegensatz zum AVL-Algorithmus). Er ist ein binärer Sortierbaum und hat die folgenden Eigenschaften: Er ist ein leerer Baum oder es Der absolute Wert des Höhenunterschieds zwischen dem linken und dem rechten Teilbaum überschreitet nicht 1, und der linke und der rechte Teilbaum sind beide ausgeglichene Binärbäume.
Weitere Informationen zu diesem Thema finden Sie auf der
chinesischen PHP-WebsiteDas obige ist der detaillierte Inhalt vonEin bestimmter Binärbaum hat 5 Knoten mit Grad 2. Wie viele Blattknoten hat dieser Binärbaum?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

