Was sind die Sortieralgorithmen von Python?

Was sind die Sortieralgorithmen in Python? Der folgende Artikel stellt Ihnen die zehn besten klassischen Sortieralgorithmen in Python vor. Es hat einen gewissen Referenzwert. Freunde in Not können sich darauf beziehen. Ich hoffe, es wird für alle hilfreich sein.

Jetzt können viele Dinge durch Algorithmen gelöst werden. Durch die Kapselung von Algorithmen mit Funktionen wird das Programm besser aufgerufen, ohne dass wiederholt geschrieben werden muss.

Zehn klassische Algorithmen von Python:

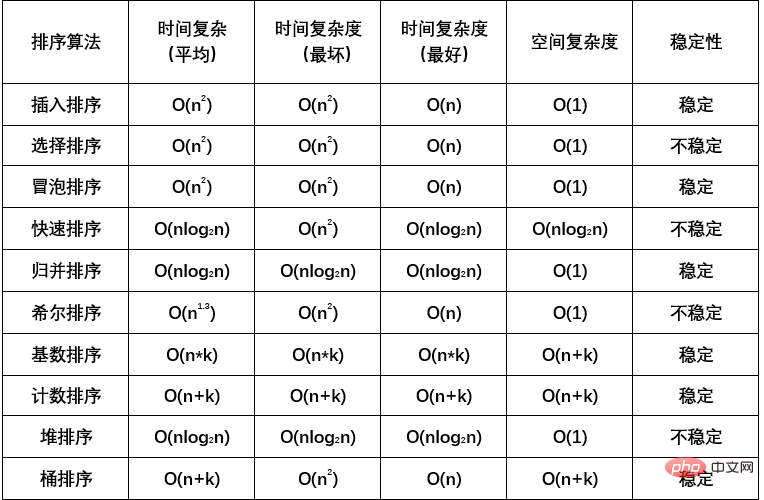
1 🎜>

1. Algorithmusidee

Beginnen Sie mit dem zweiten Element und vergleichen Sie es mit dem vorherigen Element , dann Verschieben Sie das vorherige Element nach hinten und das aktuelle Element nacheinander nach vorne, bis ein Element gefunden wird, das kleiner oder gleich ist und dahinter eingefügt wird.

Wählen Sie dann das dritte Element aus, wiederholen Sie den obigen Vorgang und fügen Sie es ein , und wählen Sie nacheinander aus. Das letzte Element schließt nach dem Einfügen die gesamte Sortierung ab.

2. Code-Implementierung

def insertion_sort(arr):
    #插入排序
    # 第一层for表示循环插入的遍数
    for i in range(1, len(arr)):
        # 设置当前需要插入的元素
        current = arr[i]
        # 与当前元素比较的比较元素
        pre_index = i - 1
        while pre_index >= 0 and arr[pre_index] > current:
            # 当比较元素大于当前元素则把比较元素后移
            arr[pre_index + 1] = arr[pre_index]
            # 往前选择下一个比较元素
            pre_index -= 1
        # 当比较元素小于当前元素，则将当前元素插入在 其后面
        arr[pre_index + 1] = current
    return arr

2. Auswahlsortierung

1. Algorithmusidee

Angenommen, das erste Element ist das Vergleichselement, vergleichen Sie es nacheinander mit den folgenden Elementen, finden Sie nach dem Vergleich aller Elemente das kleinste Element, tauschen Sie es gegen das erste Element aus und wiederholen Sie den obigen Vorgang Wir finden das zweitkleinste Element und tauschen es mit dem Element an der zweiten Position aus, und so weiter, um das verbleibende kleinste Element zu finden und es nach vorne zu verschieben, das heißt, die Sortierung ist abgeschlossen.

2. Code-Implementierung

def selection_sort(arr):
    #选择排序
    # 第一层for表示循环选择的遍数
    for i in range(len(arr) - 1):
        # 将起始元素设为最小元素
        min_index = i
        # 第二层for表示最小元素和后面的元素逐个比较
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_index]:
                # 如果当前元素比最小元素小，则把当前元素角标记为最小元素角标
                min_index = j
        # 查找一遍后将最小元素与起始元素互换
        arr[min_index], arr[i] = arr[i], arr[min_index]
    return arr

3. Blasensortierung

1 . Algorithmusidee

Beginnen Sie mit dem Vergleich der ersten und zweiten. Wenn die erste größer als die zweite ist, tauschen Sie die Positionen, vergleichen Sie dann die zweite und dritte und gehen Sie nach und nach zurück In der ersten Runde wurde das größte Element als letztes eingestuft.

Wenn der obige Vorgang also wiederholt wird, wird das zweitgrößte Element als vorletztes eingestuft. , und wiederholen Sie dann den obigen Vorgang n-1 Mal, um die Sortierung abzuschließen, da es beim letzten Mal nur ein Element gab und daher kein Vergleich erforderlich ist.

2. Code-Implementierung

def bubble_sort(arr):
    #冒泡排序
    # 第一层for表示循环的遍数
    for i in range(len(arr) - 1):
        # 第二层for表示具体比较哪两个元素
        for j in range(len(arr) - 1 - i):
            if arr[j] > arr[j + 1]:
                # 如果前面的大于后面的，则交换这两个元素的位置
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

Schnelle Sortierung

1. Algorithmische Idee

Finden Sie die Grundbedingung, die so einfach wie möglich sein muss, und zerlegen Sie das Problem weiter (oder reduzieren Sie die Größe), bis die Grundbedingung erfüllt ist.

2. Code-Implementierung

def quick_sort(arr):
  if len(arr) < 2:
    # 基线条件：为空或只包含一个元素的数组是“有序”的
    return arr
  else:
    # 递归条件
    pivot = arr[0]
    # 由所有小于基准值的元素组成的子数组
    less = [i for i in arr[1:] if i <= pivot]
    # 由所有大于基准值的元素组成的子数组
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)

print(quick_sort([10, 5, 2, 3]))

5. Zusammenführungssortierung

1. Algorithmusidee

Merge-Sortierung ist eine typische Anwendung der Divide-and-Conquer-Methode. Divide-and-Conquer-Methode (Pide-and-Conquer): Teilen Sie das ursprüngliche Problem in n kleinere Teilprobleme mit ähnlichen Strukturen wie das ursprüngliche Problem auf und kombinieren Sie dann die Ergebnisse, um die Lösung des ursprünglichen Problems zu erhalten . Die zerlegte Sequenz sieht aus wie ein Binärbaum.

Spezifische Implementierungsschritte:

1. Verwenden Sie Rekursion, um die Quellsequenz mithilfe der Dichotomiemethode in mehrere Teilsequenzen zu unterteilen

2. Beantragen Sie Platz zum Teilen der beiden Unterspalten Sortieren und Zusammenführen und kehren Sie dann zurück

3. Führen Sie alle Unterspalten Schritt für Schritt zusammen und schließen Sie schließlich die Sortierung ab

Hinweis: Zuerst zerlegen und dann zusammenführen

2. Code-Implementierung

6. Hill-Sortierung

1. Algorithmusidee

Die Gesamtidee der Hill-Sortierung besteht darin, mehrere Elemente in einem festen Intervall zu sortieren und dann das Intervall zu reduzieren. Auf diese Weise wird die endgültige Sequenz zu einer grundlegenden geordneten Sequenz.

Spezifische Schritte:

Berechnen Sie einen Inkrementwert (Intervallwert)

1. Vergleichen Sie Elemente mit Inkrementen, z. B. wenn die Der Inkrementwert ist 7, dann fügen Sie die Sortierelemente 0, 7, 14, 21... ein

2. und sortieren Sie dann 1, 8, 15... und sortieren Sie sie in aufsteigender Reihenfolge.

3. Nachdem alle Elemente sortiert sind, reduzieren Sie die Schrittweite auf beispielsweise 3 und wiederholen Sie dann die Schritte 2 und 3 oben

4. Zum Schluss reduzieren die Erhöhung um 1, die Reihenfolge ist grundsätzlich in Ordnung, und die letzte normale Einfügung kann durchgeführt werden
2. Code-Implementierung

def merge_sort(arr):
    #归并排序
    if len(arr) == 1:
        return arr
    # 使用二分法将数列分两个
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]
    # 使用递归运算
    return marge(merge_sort(left), merge_sort(right))


def marge(left, right):
    #排序合并两个数列
    result = []
    # 两个数列都有值
    while len(left) > 0 and len(right) > 0:
        # 左右两个数列第一个最小放前面
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    # 只有一个数列中还有值，直接添加
    result += left
    result += right
    return result

7. Radix-Sortierung

1. Algorithmus-Idee

Radix-Sortierung (Radix-Sortierung) gehört zur „Verteilungssortierung“. Wie der Name schon sagt, wird es auch als „Bucket-Sortierung“ oder „Bin-Sortierung“ bezeichnet und ordnet die zu sortierenden Elemente anhand eines Teils der Schlüsselwertinformationen bestimmten „Buckets“ zu, um den Sortiereffekt zu erzielen. Radix-Sortiermethode Es handelt sich um eine stabile Sortierung. und seine Zeitkomplexität beträgt O (nlog(r)m), wobei r die genommene Basis und m die Anzahl der Heaps ist. Manchmal ist die Effizienz der Basis-Sortiermethode höher als bei anderen stabilen Methoden .

2. Code-Implementierung

2.1 wird von der Bucket-Sortierung vom niedrigsten zum höchsten Bit umgewandelt und schließlich die endgültige Rangliste ausgegeben.

def shell_sort(arr):
    #希尔排序
    # 取整计算增量（间隔）值
    gap = len(arr) // 2
    while gap > 0:
        # 从增量值开始遍历比较
        for i in range(gap, len(arr)):
            j = i
            current = arr[i]
            # 元素与他同列的前面的每个元素比较，如果比前面的小则互换
            while j - gap >= 0 and current < arr[j - gap]:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = current
        # 缩小增量（间隔）值
        gap //= 2
    return arr

2.2 Einfache Implementierung

from random import randint
def radix_sort():
  A = [randint(1, 99999999) for _ in xrange(9999)]
  for k in xrange(8):
    S = [ [] for _ in xrange(10)]
    for j in A:
      S[j / (10 ** k) % 10].append(j)
    A = [a for b in S for a in b]
  for i in A:
    print i

八、计数排序

1.算法思想

对每一个输入元素x，确定小于x的元素个数。利用这一信息，就可以直接把x 放在它在输出数组上的位置上了，运行时间为O(n)，但其需要的空间不一定，空间浪费大。

2.代码实现

from numpy.random import randint
def Conuting_Sort(A):
    k = max(A)          # A的最大值，用于确定C的长度
    C = [0]*(k+1)       # 通过下表索引，临时存放A的数据
    B = (len(A))*[0]    # 存放A排序完成后的数组
    for i in range(0, len(A)):
        C[A[i]] += 1    # 记录A有哪些数字，值为A[i]的共有几个
    for i in range(1, k+1):
        C[i] += C[i-1]  # A中小于i的数字个数为C[i]
    for i in range(len(A)-1, -1, -1):
        B[C[A[i]]-1] = A[i] # C[A[i]]的值即为A[i]的值在A中的次序
        C[A[i]] -= 1    # 每插入一个A[i]，则C[A[i]]减一
    return B

九、堆排序

1.算法思想

堆分为最大堆和最小堆，是完全二叉树。堆排序就是把堆顶的最大数取出，将剩余的堆继续调整为最大堆,具体过程在第二块有介绍，以递归实现 ，

剩余部分调整为最大堆后,再次将堆顶的最大数取出，再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。

2.代码实现

import time,random
def sift_down(arr, node, end):
    root = node
    #print(root,2*root+1,end)
    while True:
        # 从root开始对最大堆调整
        child = 2 * root +1  #left child
        if child  > end:
            #print('break',)
            break
        print("v:",root,arr[root],child,arr[child])
        print(arr)
        # 找出两个child中交大的一个
        if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
            child += 1 #设置右边为大
        if arr[root] < arr[child]:
            # 最大堆小于较大的child, 交换顺序
            tmp = arr[root]
            arr[root] = arr[child]
            arr[child]= tmp
            # 正在调整的节点设置为root
            #print("less1:", arr[root],arr[child],root,child)
            root = child #
            #[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
            #print("less2:", arr[root],arr[child],root,child)
        else:
            # 无需调整的时候, 退出
            break
    #print(arr)
    print(&#39;-------------&#39;)
 
def heap_sort(arr):
    # 从最后一个有子节点的孩子还是调整最大堆
    first = len(arr) // 2 -1
    for i in range(first, -1, -1):
        sift_down(arr, i, len(arr) - 1)
    #[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
    print(&#39;--------end---&#39;,arr)
    # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
    for end in range(len(arr) -1, 0, -1):
        arr[0], arr[end] = arr[end], arr[0]
        sift_down(arr, 0, end - 1)
        #print(arr)

十、桶排序

1.算法思想

为了节省空间和时间，我们需要指定要排序的数据中最小以及最大的数字的值，来方便桶排序算法的运算。

2.代码实现

#桶排序
def bucket_sort(the_list):
    #设置全为0的数组
    all_list = [0 for i in range(100)]
    last_list = []
    for v in the_list:
        all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
    for i,t_v in enumerate(all_list):
        if t_v != 0:
            for j in range(t_v):
                last_list.append(i)
    return last_list

 总结：

在编程中，算法都是相通的，算法重在算法思想，相当于将一道数学上的应用题的每个条件，区间，可能出现的结果进行分解，分步骤的实现它。算法就是将具体问题的共性抽象出来，将步骤用编程语言来实现。通过这次对排序算法的整理，加深了对各算法的了解，具体的代码是无法记忆的，通过对算法思想的理解，根据伪代码来实现具体算法的编程，才是真正了解算法。

推荐学习：Python视频教程

Das obige ist der detaillierte Inhalt vonWas sind die Sortieralgorithmen von Python?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!