Binärbaum, dynamische Programmierung und Backtracking-Methode in JavaScript (Fallanalyse)

Ich habe es eilig geschrieben. In Bezug auf Speicher und Effizienz gibt es jedoch noch viele Bereiche, die verbessert werden müssen. Bitte geben Sie mir weitere Ratschläge.

Problembeschreibung

Bei einem Binärbaum ist der Wurzelknoten Ebene 1 und die Tiefe 1. Hängen Sie eine Reihe von Knoten mit dem Wert v an ihre d-te Ebene an.

Fügen Sie eine Regel hinzu: Erstellen Sie bei einem gegebenen Tiefenwert d (positive ganze Zahl) für jeden nicht leeren Knoten N in der Tiefe d-1-Ebene zwei linke Teilbäume und rechte Teilbäume mit den Werten v für N-Baum.

Verbinden Sie den ursprünglichen linken Teilbaum von N mit dem linken Teilbaum des neuen Knotens v.

Verbinden Sie den ursprünglichen rechten Teilbaum von N mit dem rechten Teilbaum des neuen Knotens v.

Wenn der Wert von d 1 ist und die Tiefe d - 1 nicht existiert, wird ein neuer Wurzelknoten v erstellt und der ursprüngliche Gesamtbaum dient als linker Teilbaum von v.

Beispiel

[Verwandte Kursempfehlungen: JavaScript-Video-Tutorial]

Input: 
A binary tree as following:       4
     /   \    2     6
   / \   / 
  3   1 5   v = 1d = 2Output: 
       4
      / \     1   1
    /     \   2       6
  / \     / 
 3   1   5

Grundidee

Durchquerung des Binärbaums vorbestellen

Die Grundstruktur des Codes

ist nicht die endgültige Struktur, sondern die allgemeine Struktur

/**
 * @param {number} cd:current depth,递归当前深度
 * @param {number} td:target depth, 目标深度
 */
var traversal = function (node, v, cd, td) {
    // 递归到目标深度，创建新节点并返回
  if (cd === td) {
    // return 新节点
  }
  // 向左子树递归
  if (node.left) {
    node.left = traversal (node.left, v, cd + 1, td);
  }
  // 向右子树递归
  if (node.right) {
    node.right = traversal (node.right, v, cd + 1, td);
  }
  // 返回旧节点
  return node;
};
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} v
 * @param {number} d
 * @return {TreeNode}
 */
var addOneRow = function (root, v, td) {
    // 从根节点开始递归
  traversal (root, v, 1, td);
  return root;
};

Detaillierte Analyse

Wir können die Diskussion einteilen und in drei Situationen behandeln

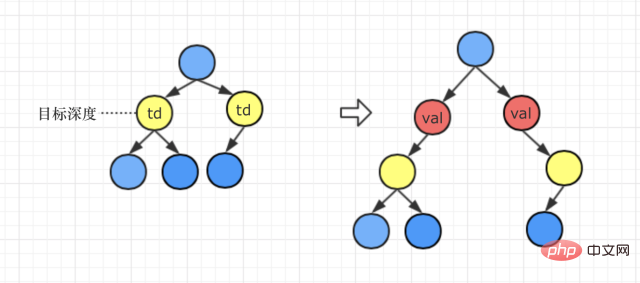
Szenario 1: Zieltiefe

Verarbeitungsmethode: Der Val-Knoten ersetzt den Knoten, der der Zieltiefe entspricht, und

● Wenn der Zielknoten ursprünglich der linke Teilbaum ist, dann das Ziel Knoten ist nach dem Zurücksetzen der linke Teilbaum des Val-Knotens

● Wenn der Zielknoten ursprünglich der rechte Teilbaum ist, dann ist der Zielknoten nach dem Zurücksetzen der rechte Teilbaum des Val-Knotens

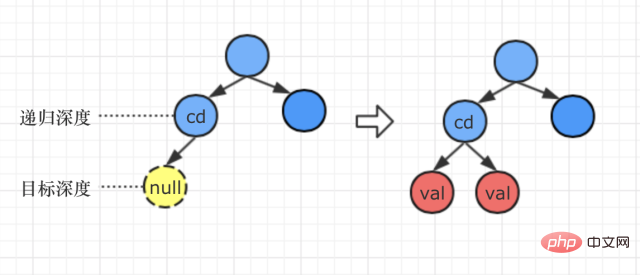
2 Situationen: Zieltiefe > die maximale Tiefe des aktuellen rekursiven Pfads

Als ich die Frage las, stellte ich fest, dass es eine solche Beschreibung gibt: „Der Bereich von Der Eingabetiefenwert d ist: [1, die maximale Tiefe des Binärbaums + 1]“

Wenn also die Zieltiefe zufällig eine Ebene tiefer ist als die Tiefe des Baums auf dem aktuellen Pfad, Die Verarbeitungsmethode lautet:

Fügen Sie neue linke und rechte Zweige des Knotenval-Knotens der unteren Ebene hinzu

Fall 3: Die Zieltiefe beträgt 1

Lassen Sie uns die Bedeutung der Frage noch einmal analysieren. Die Frage lautet: „Wenn der Wert von d 1 ist und die Tiefe d – 1 nicht existiert, wird ein neuer Wurzelknoten v erstellt Der ursprüngliche Gesamtbaum wird als linker Teilbaum von v verwendet 🎜>

Alle Codes

/**
 * @param {v} val,插入节点携带的值
 * @param {cd} current depth,递归当前深度
 * @param {td} target depth, 目标深度
 * @param {isLeft}  判断原目标深度的节点是在左子树还是右子树
 */
var traversal = function (node, v, cd, td, isLeft) {
  debugger;
  if (cd === td) {
    const newNode = new TreeNode (v);
    // 如果原来是左子树，重置后目标节点还是在左子树上，否则相反
    if (isLeft) {
      newNode.left = node;
    } else {
      newNode.right = node;
    }
    return newNode;
  }
  // 处理上述的第1和第2种情况
  if (node.left || (node.left === null && cd + 1 === td)) {
    node.left = traversal (node.left, v, cd + 1, td, true);
  }
  if (node.right || (node.right === null && cd + 1 === td)) {
    node.right = traversal (node.right, v, cd + 1, td, false);
  }
  return node;
};
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} v
 * @param {number} d
 * @return {TreeNode}
 */
var addOneRow = function (root, v, td) {
  // 处理目标深度为1的情况，也就是上述的第3种情况
  if (td === 1) {
    const n = new TreeNode (v);
    n.left = root;
    return n;
  }
  traversal (root, v, 1, td);
  return root;
};

Wortaufteilung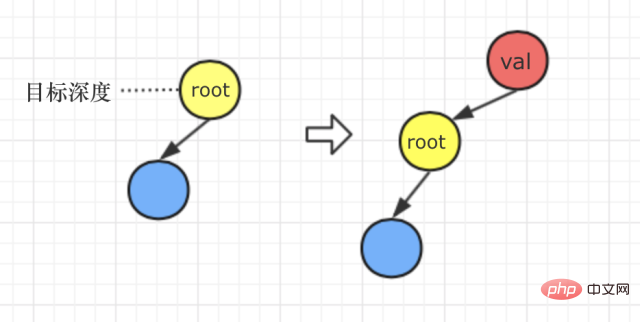

Problembeschreibung

Gegeben eine nicht leere Zeichenfolge s und Ein Wörterbuch wordDict, das eine nicht leere Wortliste enthält, bestimmt, ob s durch Leerzeichen in ein oder mehrere Wörter aufgeteilt werden kann, die im Wörterbuch erscheinen.

Anleitung:

1. Wörter im Wörterbuch können beim Teilen wiederverwendet werden.

2.你可以假设字典中没有重复的单词。

Example 

example1
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
注意: 你可以重复使用字典中的单词。

example2
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/word-break

基本思想 

动态规划

具体分析

动态规划的关键点是：寻找状态转移方程

有了这个状态转移方程，我们就可以根据上一阶段状态和决策结果，去求出本阶段的状态和结果

然后，就可以从初始值，不断递推求出最终结果。

在这个问题里，我们使用一个一维数组来存放动态规划过程的递推数据

假设这个数组为dp，数组元素都为true或者false,

dp[N] 存放的是字符串s中从0到N截取的子串是否是“可拆分”的布尔值

让我们从一个具体的中间场景出发来思考计算过程

假设我们有

wordDict = ['ab','cd','ef']
s ='abcdef'

并且假设目前我们已经得出了N=1到N=5的情况，而现在需要计算N=6的情况

或者说，我们已经求出了dp[1] 到dp[5]的布尔值，现在需要计算dp[6] = ?

该怎么计算呢？

现在新的字符f被加入到序列“abcde”的后面，如此以来，就新增了以下几种6种需要计算的情况

A序列 + B序列1.abcdef + ""
2.abcde + f3.abcd + ef4.abc + def5.ab + cdef6.a + bcdef
注意：当A可拆且B可拆时，则A+B也是可拆分的

从中我们不难发现两点

1. 当A可拆且B可拆时，则A+B也是可拆分的

2. 这6种情况只要有一种组合序列是可拆分的，abcdef就一定是可拆的，也就得出dp[6] = true了

下面是根据根据已有的dp[1] 到dp[5]的布尔值，动态计算dp[6] 的过程

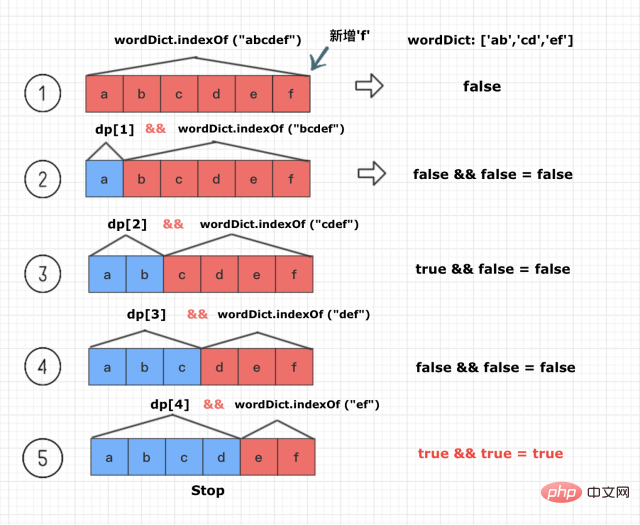
（注意只要计算到可拆，就可以break循环了）

具体代码

var initDp = function (len) {
  let dp = new Array (len + 1).fill (false);
  return dp;
};
/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {boolean}
 */
var wordBreak = function (s, wordDict) {
  // 处理空字符串
  if (s === '' && wordDict.indexOf ('') === -1) {
    return false;
  }
  const len = s.length;
  // 默认初始值全部为false
  const dp = initDp (len);
  const a = s.charAt (0);
  // 初始化动态规划的初始值
  dp[0] = wordDict.indexOf (a) === -1 ? false : true;
  dp[1] = wordDict.indexOf (a) === -1 ? false : true;
  // i:end
  // j:start
  for (let i = 1; i < len; i++) {
    for (let j = 0; j <= i; j++) {
      // 序列[0,i] = 序列[0,j] + 序列[j,i]
      // preCanBreak表示序列[0,j]是否是可拆分的
      const preCanBreak = dp[j];
      // 截取序列[j,i]
      const str = s.slice (j, i + 1);
      // curCanBreak表示序列[j,i]是否是可拆分的
      const curCanBreak = wordDict.indexOf (str) !== -1;
      // 情况1: 序列[0,j]和序列[j,i]都可拆分，那么序列[0,i]肯定也是可拆分的
      const flag1 = preCanBreak && curCanBreak;
      // 情况2: 序列[0,i]本身就存在于字典中，所以是可拆分的
      const flag2 = curCanBreak && j === 0;
      if (flag1 || flag2) {
        // 设置bool值，本轮计算结束
        dp[i + 1] = true;
        break;
      }
    }
  }
  // 返回最后结果
  return dp[len];
};

全排列

题目描述

给定一个没有重复数字的序列，返回其所有可能的全排列。

Example

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

基本思想

回溯法

具体分析

1. 深度优先搜索搞一波，index在递归中向前推进

2. 当index等于数组长度的时候，结束递归，收集到results中（数组记得要深拷贝哦）

3. 两次数字交换的运用，计算出两种情况

总结

想不通没关系，套路一波就完事了

具体代码

var swap = function (nums, i, j) {
  const temp = nums[i];
  nums[i] = nums[j];
  nums[j] = temp;
};

var recursion = function (nums, results, index) {
  // 剪枝
  if (index >= nums.length) {
    results.push (nums.concat ());
    return;
  }
  // 初始化i为index
  for (let i = index; i < nums.length; i++) {
    // index 和 i交换？？
    // 统计交换和没交换的两种情况
    swap (nums, index, i);
    recursion (nums, results, index + 1);
    swap (nums, index, i);
  }
};
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
  const results = [];
  recursion (nums, results, 0);
  return results;
};

本文来自 js教程 栏目，欢迎学习！  

Das obige ist der detaillierte Inhalt vonBinärbaum, dynamische Programmierung und Backtracking-Methode in JavaScript (Fallanalyse). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!