Warum wählt MySQL den B+-Baum als Indexstruktur? (ausführliche Erklärung)

In MySQL verwenden sowohl Innodb als auch MyIsam den B+-Baum als Indexstruktur (andere Indizes wie Hash werden hier nicht berücksichtigt). Dieser Artikel beginnt mit dem häufigsten binären Suchbaum und erläutert nach und nach die von verschiedenen Bäumen gelösten Probleme sowie die neuen Probleme, mit denen er konfrontiert ist. Dabei wird erklärt, warum MySQL den B + -Baum als Indexstruktur wählt.

Ein oder zwei binäre Suchbäume (BST): unausgeglichen

Der binäre Suchbaum (BST, Binary Search Tree), auch binärer Sortierbaum genannt, muss auf der Grundlage des Binärbaums Folgendes erfüllen: Der Wert aller Knoten im linken Teilbaum eines Knotens ist nicht größer als der Wert des Wurzelknoten, beliebiger Knoten Der Wert aller Knoten im rechten Teilbaum ist nicht kleiner als der Wert des Wurzelknotens. Das Folgende ist ein BST (Bildquelle).

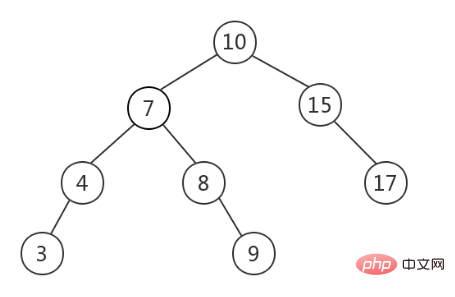
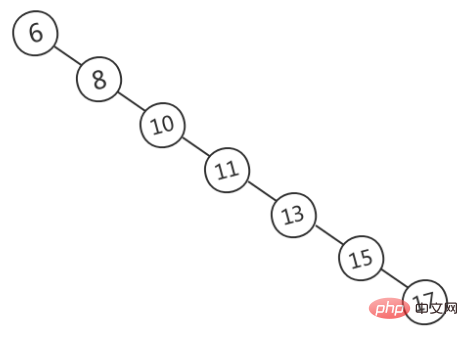
Wenn eine schnelle Suche erforderlich ist, ist das Speichern von Daten in BST eine häufige Wahl, da zu diesem Zeitpunkt die Abfragezeit von der Baumhöhe abhängt und die durchschnittliche Zeitkomplexität O beträgt (lgn). BST kann jedoch verzerrt werden und unausgeglichen werden, wie in der Abbildung unten (Bildquelle) dargestellt. Zu diesem Zeitpunkt degeneriert BST zu einer verknüpften Liste und die Zeitkomplexität degeneriert An).

Um dieses Problem zu lösen, werden ausgeglichene Binärbäume eingeführt.

2. Balanced Binary Tree (AVL): Rotation zeitaufwändig

AVL-Baum ist streng ausgeglichen Bei Binärbäumen darf der Höhenunterschied zwischen den linken und rechten Teilbäumen aller Knoten 1 nicht überschreiten; AVL-Baumsuche, -einfügung und -löschung betragen im Durchschnitt und im schlechtesten Fall O(lgn).

Der Schlüssel zum Erreichen des Gleichgewichts in AVL liegt in der Rotationsoperation: Einfügen und Löschen können das Gleichgewicht des Binärbaums zerstören. In diesem Fall muss der Baum durch eine oder mehrere Baumrotationen neu ausgeglichen werden. Beim Einfügen von Daten ist höchstens eine Rotation (einfache Rotation oder doppelte Rotation) erforderlich. Wenn Daten jedoch gelöscht werden, gerät die AVL ins Ungleichgewicht aller Knoten auf dem Pfad vom gelöschten Knoten zum Wurzelknoten. Die Größe beträgt O(lgn).

Aufgrund der zeitaufwändigen Rotation ist der AVL-Baum beim Löschen von Daten sehr ineffizient.Bei vielen Löschvorgängen können die Kosten für die Aufrechterhaltung des Gleichgewichts anfallen höher als der Nutzen, sodass AVL in der Praxis nicht weit verbreitet ist.

3. Rot-schwarzer Baum: Der Baum ist zu hochIm Vergleich zum AVL-Baum strebt der rot-schwarze Baum kein striktes Gleichgewicht an , ist aber eine grobe Abwägung: Stellen Sie einfach sicher, dass der längstmögliche Weg von der Wurzel zum Blatt nicht mehr als doppelt so lang ist wie der kürzestmögliche Weg. Aus Sicht der Implementierung besteht das größte Merkmal des Rot-Schwarz-Baums darin, dass jeder Knoten zu einer von zwei Farben (Rot oder Schwarz) gehört und die Aufteilung der Knotenfarben bestimmte Regeln erfüllen muss (die spezifischen Regeln werden weggelassen). . Ein Beispiel für einen rot-schwarzen Baum ist wie folgt (Bildquelle):

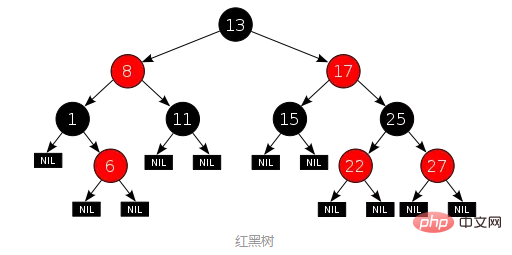Im Vergleich zu einem AVL-Baum nimmt die Abfrageeffizienz eines rot-schwarzen Baums ab liegt daran, dass sich das Gleichgewicht des Baumes durch die höhere Höhe verändert. Die Löscheffizienz des Rot-Schwarz-Baums wurde jedoch erheblich verbessert, da der Rot-Schwarz-Baum auch Farbe einführt. Beim Einfügen oder Löschen von Daten sind nur O(1) Rotations- und Farbänderungen erforderlich, um das Grundgleichgewicht sicherzustellen Es besteht keine Notwendigkeit für AVL. Der Baum führt eine O(lgn)-Anzahl von Umdrehungen durch. Im Allgemeinen ist die statistische Leistung rot-schwarzer Bäume höher als die von AVL.

Daher werden AVL-Bäume in praktischen Anwendungen relativ selten verwendet, während rot-schwarze Bäume sehr häufig verwendet werden. Beispielsweise verwendet TreeMap in Java rot-schwarze Bäume, um sortierte Schlüssel-Wert-Paare zu speichern; HashMap in Java8 verwendet verknüpfte Listen + rot-schwarze Bäume, um Hash-Konfliktprobleme zu lösen (wenn weniger widersprüchliche Knoten vorhanden sind, verwenden Sie verknüpfte Listen; wenn vorhanden). Für mehr widersprüchliche Knoten verwenden Sie den roten schwarzen Baum.

In Situationen, in denen sich Daten im Speicher befinden (wie die oben erwähnte TreeMap und HashMap), ist die Leistung von Rot-Schwarz-Bäumen sehr gut. Aber

für den Fall, dass sich die Daten auf Hilfsspeichergeräten wie Festplatten (wie

MySQL und anderen Datenbanken) befinden, ist der Rot-Schwarz-Baum nicht gut darin, weil der rotschwarze Baum immer noch zu hoch wächst . Wenn sich die Daten auf der Festplatte befinden, wird Festplatten-E/A zum größten Leistungsengpass. Das Entwurfsziel sollte darin bestehen, die Anzahl der E/A-Zeiten zu minimieren, je höher die Höhe des Baums, desto mehr E/A-Zeiten sind für Hinzufügungen, Löschungen und Änderungen erforderlich und Suchvorgänge, die die Leistung erheblich beeinträchtigen.

4. B-Baum: Geboren für Scheiben

B

Baum wird auch B-Baum (wobei - kein Minuszeichen ist) ist ein in mehrere Richtungen ausgewogener Suchbaum, der für Hilfsspeichergeräte wie Festplatten, Im Vergleich zu Binärbäumen kann jeder Nicht-Blattknoten des B-Baums mehrere Unterbäume haben. Wenn die Gesamtzahl der Knoten gleich ist, ist die Höhe des B-Baums daher viel kleiner als die des AVL-Baums und des rot-schwarzen Baums (der B-Baum ist ein „Zwerg“) und die Anzahl der Festplatten-IOs wird stark reduziert.

Das wichtigste Konzept bei der Definition eines B-Baums ist die Ordnung. Für einen B-Baum der Ordnung m müssen die folgenden Bedingungen erfüllt sein:

• Jeder Knoten enthält höchstens m untergeordnete Knoten .
• Wenn der Wurzelknoten untergeordnete Knoten enthält, enthält er mindestens 2 untergeordnete Knoten. Mit Ausnahme des Wurzelknotens enthält jeder Nicht-Blattknoten mindestens m/2 untergeordnete Knoten.
• Ein Nicht-Blattknoten mit k Kindern enthält k – 1 Datensätze.
• Alle Blattknoten befinden sich in derselben Ebene.

Es ist ersichtlich, dass die Definition des B-Baums hauptsächlich die Anzahl der untergeordneten Knoten und Datensätze von Nicht-Blattknoten begrenzt.

Das Bild unten ist ein Beispiel für einen B-Baum 3. Ordnung (Bildquelle):

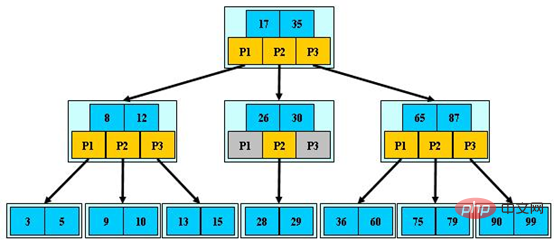
Die Vorteile des B-Baums sind nicht nur gering Baumhöhe, aber auch die Fähigkeit, auf lokale Teile zuzugreifen Nutzung sexueller Prinzipien. Das sogenannte Lokalitätsprinzip bedeutet, dass bei der Verwendung eines Datenelements die nahegelegenen Daten eine höhere Wahrscheinlichkeit haben, in kurzer Zeit verwendet zu werden. B-Tree speichert Daten mit ähnlichen Schlüsseln im selben Knoten. Wenn auf einen der Daten zugegriffen wird, liest die Datenbank den gesamten Knoten sofort in den Cache. Es ist keine Festplatten-E/A erforderlich. Mit anderen Worten: Die Cache-Trefferrate von B-Tree ist höher.

B-Tree hat einige Anwendungen in Datenbanken. Beispielsweise verwendet der Index von Mongodb die B-Tree-Struktur. In vielen Datenbankanwendungen werden jedoch B+-Bäume, eine Variante des B-Baums, verwendet.

5. B+-Baum

B+-Baum ist auch ein mehrpfadiger, ausgeglichener Suchbaum. Sein Hauptunterschied zum B-Baum ist:

• Jeder Knoten im B-Baum (einschließlich Blattknoten und Nicht-Blattknoten) speichert echte Daten. Nur Blattknoten im B+-Baum speichern echte Daten und Nicht-Blattknoten speichern nur Schlüssel. In MySQL können die hier genannten realen Daten alle Daten der Zeile sein (z. B. der Clustered-Index von Innodb) oder nur der Primärschlüssel der Zeile (z. B. der Hilfsindex von Innodb) oder die Adresse der Zeile ( wie der nicht gruppierte Index von MyIsam).
• Ein Datensatz im B-Baum erscheint nur einmal und nicht wiederholt, während der Schlüssel des B+-Baums wiederholt erscheinen kann – er wird definitiv in einem Blattknoten erscheinen, oder er kann wiederholt in einem Nicht-Baum erscheinen -Blattknoten.
• Die Blattknoten des B+-Baums sind durch eine doppelt verknüpfte Liste verknüpft.
• Für Nicht-Blattknoten im B-Baum ist die Anzahl der Datensätze um 1 kleiner als die Anzahl der untergeordneten Knoten, während die Anzahl der Datensätze im B+-Baum gleich der Anzahl der untergeordneten Knoten ist.

Somit hat der B+-Baum die folgenden Vorteile gegenüber dem B-Baum:

• Weniger IO-Zeiten: Die Nicht- Die Blattknoten des B+-Baums enthalten nur Schlüssel, keine realen Daten, sodass die Anzahl der in jedem Knoten gespeicherten Datensätze viel größer ist als die Anzahl von B (dh die Reihenfolge m ist größer), sodass die Höhe des B+-Baums gleich ist niedriger und die Zugriffszeit ist geringer. Es sind weniger E/A-Zeiten erforderlich. Da außerdem jeder Knoten mehr Datensätze speichert, wird das Zugriffslokalitätsprinzip besser genutzt und die Cache-Trefferquote ist höher.
• ist besser für Bereichsabfragen geeignet: Wenn Sie eine Bereichsabfrage in einem B-Baum durchführen, suchen Sie zuerst die zu findende untere Grenze und führen Sie dann einen In durch -Ordnungsdurchlauf des B-Baums bis Finden Sie die Obergrenze der Suche, und die Bereichsabfrage des B + -Baums muss nur die verknüpfte Liste durchlaufen.
• Stabilere Abfrageeffizienz: Die Abfragezeitkomplexität des B-Baums liegt zwischen 1 und der Baumhöhe (entsprechend dem Wurzelknoten bzw. Blattknoten). Die Abfragekomplexität des B+-Baums ist auf der Baumhöhe stabil, da sich alle Daten in den Blattknoten befinden.

B+-Bäume haben auch Nachteile: Da Schlüssel wiederholt auftauchen, nehmen sie mehr Platz ein. Im Vergleich zu den Leistungsvorteilen ist der Platznachteil jedoch oft akzeptabel, sodass B+-Bäume in Datenbanken häufiger verwendet werden als B-Bäume.

6. Spüren Sie die Kraft des B+-Baums

Wie bereits erwähnt, im Vergleich zu binären Bäumen wie Rot-Schwarz-Bäumen, B-Baum Der /B+-Baum ist am größten. Der Vorteil besteht darin, dass die Baumhöhe kleiner ist. Tatsächlich beträgt die Höhe des Baums für den B + -Index von Innodb im Allgemeinen 2 bis 4 Ebenen. Lassen Sie uns einige konkrete Schätzungen vornehmen.

Die Höhe des Baums wird durch die Reihenfolge bestimmt. Je größer die Reihenfolge, desto kürzer ist der Baum. Die Größe der Reihenfolge hängt davon ab, wie viele Datensätze jeder Knoten speichern kann. Jeder Knoten in Innodb verwendet eine Seite (Seite), die Seitengröße beträgt 16 KB, von denen Metadaten nur etwa 128 Byte ausmachen (einschließlich Dateiverwaltungs-Header-Informationen, Seiten-Header-Informationen usw.), der größte Teil des Speicherplatzes wird zum Speichern von Daten verwendet .

• Für Nicht-Blattknoten enthält der Datensatz nur den Schlüssel des Index und einen Zeiger auf den Knoten der nächsten Ebene. Unter der Annahme, dass jede Nicht-Blattseite 1000 Datensätze speichert, nimmt jeder Datensatz etwa 16 Byte ein; diese Annahme ist sinnvoll, wenn der Index eine Ganzzahl oder eine kürzere Zeichenfolge ist. Im weiteren Sinne hören wir häufig Vorschläge, dass die Länge der Indexspalte nicht zu groß sein sollte. Hier ist der Grund: Wenn die Indexspalte zu lang ist und jeder Knoten zu wenige Datensätze enthält, wird der Baum zu hoch und der Indexierungseffekt wird stark reduziert und der Index wird mehr Platz verschwenden.

• Bei Blattknoten enthält der Datensatz den Schlüssel und den Wert des Index (der Wert kann der Primärschlüssel der Zeile, eine vollständige Datenzeile usw. sein, Einzelheiten finden Sie im vorherigen Artikel) und die Datenmenge ist größer. Hier wird davon ausgegangen, dass jede Blattknotenseite 100 Datensätze speichert (tatsächlich kann diese Zahl bei einem Clustered-Index kleiner als 100 sein; wenn es sich bei dem Index um einen Hilfsindex handelt, kann diese Zahl viel größer als 100 sein; dies ist möglich). basierend auf der tatsächlichen Situation geschätzt werden).

Bei einem 3-Schichten-B+-Baum hat die erste Schicht (Wurzelknoten) 1 Seite und kann 1000 Datensätze speichern; die zweite Schicht hat 1000 Seiten und kann 1000*1000 Datensätze speichern; (Blattknoten) hat 1000 * 1000 Seiten, und jede Seite kann 100 Datensätze speichern, sodass 1000 * 1000 * 100 Datensätze oder 100 Millionen Datensätze gespeichert werden können. Für einen Binärbaum sind etwa 26 Schichten erforderlich, um 100 Millionen Datensätze zu speichern.

7. Zusammenfassung

Fassen Sie abschließend die von verschiedenen Bäumen gelösten Probleme und die neuen Probleme zusammen:

1) , Binärer Suchbaum (BST): löst das grundlegende Problem der Sortierung, aber da das Gleichgewicht nicht garantiert werden kann, kann es zu einer verknüpften Liste kommen

2), Balanced Binary Tree (AVL): löst das Problem von Gleichgewicht durch Rotation, aber die Effizienz des Rotationsvorgangs ist zu niedrig.

3) Rot-Schwarz-Baum: Durch den Verzicht auf ein striktes Gleichgewicht und die Einführung von Rot-Schwarz-Knoten wird das Problem der zu niedrigen AVL-Rotationseffizienz gelöst , in Szenarien wie Festplatten ist der Baum immer noch zu hoch, zu viele E/A-Zeiten; zu hoch ist gelöst;

5), B+-Baum: Basierend auf dem B-Baum werden Nicht-Blattknoten in reine Indexknoten umgewandelt, die keine Daten speichern, wodurch die Höhe des Baums weiter reduziert wird Darüber hinaus werden die Blattknoten mithilfe von Zeigern zu einer verknüpften Liste verbunden, wodurch Bereichsabfragen effizienter werden.

Empfohlenes Lernen:

MySQL-Tutorial

Das obige ist der detaillierte Inhalt vonWarum wählt MySQL den B+-Baum als Indexstruktur? (ausführliche Erklärung). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!