Heim >häufiges Problem >Zeitkomplexität der binären Suchtechnik
Zeitkomplexität der binären Suchtechnik
- (*-*)浩Original
- 2019-10-25 10:13:0112981Durchsuche
Die binäre Suchmethode, die die Ordnungsbeziehung zwischen Elementen voll ausnutzt und die Divide-and-Conquer-Strategie übernimmt, kann die Suchaufgabe im schlimmsten Fall in O(log n) abschließen.
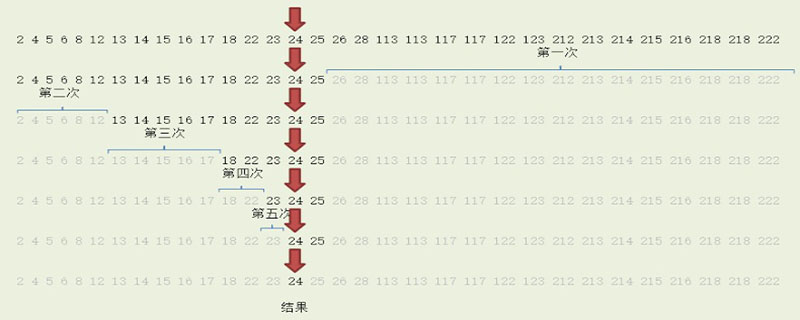
Die Grundidee besteht darin, n Elemente in zwei Hälften mit ungefähr der gleichen Zahl zu teilen und a[n/2] und die Zahl du zu nehmen Wenn x=a[n/2] ist, wird x gefunden und die Algorithmusoperation wird beendet. (Empfohlenes Lernen: Web-Frontend-Video-Tutorial)
In der Informatik wird die binäre Suche (englisch: binäre Suche), auch bekannt als Halbintervallsuche (englisch: half -Intervallsuche) , Logarithmische Suche (englisch: logarithmische Suche) ist ein Suchalgorithmus zum Suchen eines bestimmten Elements in einem geordneten Array.
Der Suchvorgang beginnt beim mittleren Element des Arrays, wenn das mittlere Element das zu findende Element ist, endet der Suchvorgang, wenn ein bestimmtes Element größer oder kleiner als das mittlere Element ist. Dann endet der Suchvorgang, wenn das Array größer oder kleiner als das mittlere Element ist. Suchen Sie in dieser Hälfte und beginnen Sie den Vergleich wie zuvor beim mittleren Element.
Wenn das Array bei einem bestimmten Schritt leer ist, bedeutet das, dass es nicht gefunden werden kann. Dieser Suchalgorithmus reduziert den Suchbereich bei jedem Vergleich um die Hälfte.
Wenn x
Die binäre Suchmethode wird sehr häufig verwendet und ihre Idee ist leicht zu verstehen, aber das Schreiben eines korrekten binären Suchalgorithmus ist keine leichte Aufgabe. Der erste binäre Suchalgorithmus erschien bereits 1946, der erste völlig korrekte binäre Suchalgorithmus erschien jedoch erst 1962.
Bentley schrieb in seinem Buch „Writing Correct Programs“, dass 90 % der Computerexperten nicht innerhalb von 2 Stunden einen völlig korrekten binären Suchalgorithmus schreiben können.
Der Schlüssel zum Problem besteht darin, die Grenzen jedes Suchbereichs genau zu formulieren, die Beendigungsbedingungen zu bestimmen und die verschiedenen Situationen mit ungeraden und geraden Zahlen richtig zusammenzufassen. Tatsächlich können wir sie finden, nachdem wir sie geklärt haben dass sein spezifischer Algorithmus sehr intuitiv ist.
Komplexitätsberechnung
Zeitkomplexität: Die binäre Suche halbiert den Suchbereich jedes Mal und es ist offensichtlich, dass die Zeitkomplexität O (log n) beträgt. (n stellt die Anzahl der Elemente in der Menge dar)
Raumkomplexität: O(1). Obwohl es in rekursiver Form definiert ist, ist es endrekursiv und kann als Schleife umgeschrieben werden.
Das obige ist der detaillierte Inhalt vonZeitkomplexität der binären Suchtechnik. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

