Heim >Datenbank >MySQL-Tutorial >Verstehen Sie die Indizes in MySQL in einem Artikel
Verstehen Sie die Indizes in MySQL in einem Artikel
- 爱喝马黛茶的安东尼nach vorne
- 2019-08-02 17:01:202164Durchsuche

Was ist ein Index?
Ein Index ist eine Datenstruktur, deren Funktion darin besteht, die Effizienz von Daten zu verbessern Abfrage. Eine gängige Metapher ist der Vergleich mit dem Katalog eines Buches. Über das Inhaltsverzeichnis können Sie genau die Seite finden, auf der sich der Inhalt eines bestimmten Kapitels befindet.
Es macht eigentlich keinen Sinn, einen Index zu verwenden, wenn die Datenmenge klein ist. Auch wenn kein Index vorhanden ist, dauert es nicht lange, bis der Computer die Daten einzeln durchläuft. Sobald die Datenmenge groß ist, ist eine Indizierung erforderlich, um sicherzustellen, dass wir normale externe Dienste bereitstellen und die Benutzererfahrung gewährleisten können.
Indextyp
Index ist eine Datenstruktur und es gibt mehrere Implementierungen, um verschiedene Szenarien zu bewältigen. In MySQL sind dies hauptsächlich Hash-Index und B+Tree.
Hash-Index
Hash Ich glaube, jeder sollte damit vertraut sein. Hash ist eine Datenstruktur in Form eines Schlüsselwerts. Die Implementierung ist im Allgemeinen eine Array + verknüpfte Listenstruktur. Die Hash-Funktion wird verwendet, um die Position des Schlüssels im Array zu berechnen. Wenn dann ein Hash-Konflikt auftritt, wird dieser über die verknüpfte Liste (Zipper-Methode) gelöst. Natürlich gibt es auch andere Möglichkeiten, Hash-Konflikte zu lösen. Die Datenstruktur von Hash wird sehr häufig verwendet. Unser System verwendet beispielsweise HashMap, um einen Hotspot-Datencache zu erstellen, und die Zugriffseffizienz ist sehr gut.
Die Hash-Struktur speichert zunächst den Hash-Wert des Schlüssels, um dessen Position im Array zu bestimmen. Bei einem Konflikt wird an der Array-Position eine verknüpfte Liste erstellt. Dies bringt offensichtlich mehrere Probleme mit sich:
Sogar die berechneten Positionen von Schlüsseln mit denselben Eigenschaften können weit voneinander entfernt sein, was kontinuierliche Abfragen ineffizient macht. Das heißt, Bereichsabfragen werden nicht unterstützt.
Der Hash-Index speichert den berechneten Hash-Wert und den Zeilenzeiger, speichert jedoch nicht den spezifischen Zeilenwert. Daher sind für die Abfrage der Daten über den Hash-Index zwei Abfragen erforderlich (erst die Position der Zeile abfragen und dann suchen). die spezifischen Daten)
Die Prämisse der Hash-Index-Abfragedaten besteht darin, den Hash-Wert zu berechnen, was bedeutet, dass der Schlüssel ein Schlüssel sein muss, der genau auf ein Datenelement verweisen kann, sodass passende Abfragen wie z like werden nicht unterstützt.
Was wir also wissen können, ist, dass der Hash-Index für die schnelle Auswahl einer bestimmten Datenzeile geeignet ist.
B+Baumstruktur
Dem Namen nach zu urteilen, ist dies offensichtlich eine Baumstruktur, die in Lehrbüchern zur Datenstruktur im College unverzichtbar ist. Die Baumstruktur ist eine besonders wichtige Datenstruktur, die an vielen Stellen verwendet wird.
Wir haben oben erwähnt, dass Hash-Indizes keine Bereichsabfragen durchführen können. Es gibt auch eine Struktur in der Baumstruktur, die für geordnete Abfragen geeignet ist – einen binären Suchbaum. Die Struktur des binären Suchbaums erfordert, dass der Wert des übergeordneten Knotens größer als der des linken untergeordneten Knotens und kleiner als der des rechten untergeordneten Knotens ist, wie unten gezeigt:
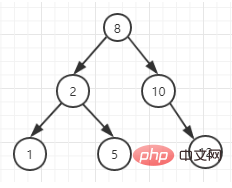
Zeit Die Komplexität der Abfrage des Binärbaums in der obigen Abbildung beträgt O(log(n)). Um die zeitliche Komplexität von O(log(n)) sicherzustellen, müssen wir natürlich sicherstellen, dass der Binärbaum jederzeit ausgeglichen bleibt .
Obwohl die Baumstruktur auch im MySQL-Index verwendet wird, handelt es sich nicht um einen Binärbaum. Da die Daten in der Datenbank letztendlich auf der Festplatte gespeichert werden und der Baum zu viele Knoten hat, dauert die Übertragung zwischen Knoten sehr lange. Bei der Implementierung von MySQL entscheiden wir uns dafür, mehr Inhalte auf demselben Knoten zu platzieren und die Vorgänge auf demselben Knoten in den Speicher zu übertragen, um die Anzahl der Übertragungen zwischen Knoten im externen Speicher zu reduzieren und so die Effizienz zu verbessern. Das ist B+Tree. Bei der Implementierung von B+Tree kann eine dreischichtige Baumstruktur grundsätzlich fast alle unsere Anforderungen erfüllen.
Verwandte Empfehlungen: „MySQL-Datenbankwissen lernen“
B-Tree
Um B+Tree zu verstehen Zunächst muss man verstehen, dass B-Tree ein ausgeglichener Baum ist und nicht „Binary“.
Der ausgeglichene Mehrpfad-Suchbaum sieht wie folgt aus:
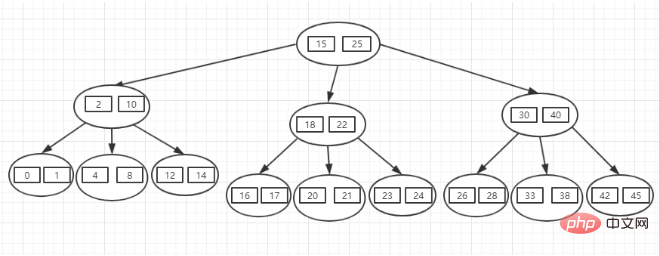
Dies ist ein 2-3-Baum, was bedeutet, dass jeder Knoten zwei Werte speichert. Die Anzahl der Zweige pro Knoten beträgt 3. Wie aus der obigen Abbildung ersichtlich ist, eignet sich die mittlere Struktur sehr gut zum Abfragen von Daten. Der Wert des linken Teilbaums jedes Knotens ist kleiner als der kleinste Wert des aktuellen Knotens, die Werte des mittleren Teilbaums liegen alle zwischen den beiden Werten des aktuellen Knotens und die Werte des rechten Teilbaums sind alle größer als der Maximalwert des aktuellen Knotens.
Zum Beispiel möchten wir den Wert 24 finden:
(1) Beurteilen Sie zunächst anhand des Wurzelknotens, dass 24 zwischen den Wurzelknoten (15, 25) liegt, also links und Rechte Teilbäume werden ausgeschlossen und die Suche erfolgt von der Mitte aus.
(2) Suchen Sie dann den Wurzelknoten (18,22) des mittleren Teilbaums. Der Vergleich ergibt, dass 24 größer als der Maximalwert des Knotens ist, mit Ausnahme des linken Teilbaums und des mittleren Teilbaums.
(3) Finden Sie den richtigen Teilbaum, stellen Sie fest, dass der Maximalwert des Knotens genau 24 beträgt, und die Abfrage endet.
Basierend auf dem obigen Prozess kann die Suche im B-Baum wie folgt zusammengefasst werden:
(1) Führen Sie ausgehend vom Wurzelknoten eine binäre Suche nach der Schlüsselwortsequenz (geordnet) innerhalb durch Knoten.
(2) Bei Treffer beenden, andernfalls den untergeordneten Knoten des Bereichs eingeben, zu dem das Abfrageschlüsselwort gehört
(3) Wiederholen Sie den obigen Vorgang, bis der entsprechende untergeordnete Knoten leer ist oder bereits ein Blattknoten ist.
Es ist ersichtlich, dass die Suchleistung einer binären Suche innerhalb des Schlüsselwortsatzes entspricht. Von hier aus scheint es, dass an B-Tree nichts auszusetzen ist, es sollte jedoch beachtet werden, dass jeder Knoten in B-Tree den Indexschlüssel und die spezifischen Zeilendaten speichert, die er darstellt. In MySQL werden die Datenbankladedaten in Seiteneinheiten geladen und die Größe jeder Seite ist fest (Standard 16 KB). Wenn jeder Knoten alle Werte speichert, gibt es nur sehr wenige Knoten, die auf einer Seite gespeichert werden können, und eine Abfrage lädt möglicherweise mehrmals Daten aus dem Speicher, was zu einer verringerten Leistung führt.
B+Tree
B+Tree ist eine Variante von B-Tree und eignet sich daher besser für die Indizierung externer Speicherdateien.
Der größte Unterschied zwischen den beiden besteht darin, dass jeder Knoten von B-Tree alle Daten speichert, während sich die Daten, die in B+Tree gespeichert werden müssen, alle auf den Blattknoten befinden und ein sequentieller Zugriffszeiger hinzugefügt wird Jeder Blattknoten hat eine Adresse, die auf den nächsten benachbarten Blattknoten zeigt. Diese Struktur stellt sicher, dass mehr Indexknoten auf einer Speicherseite gespeichert werden können, und eignet sich besser für Bereichsabfragen.
Index
Da die Speicher-Engine für die Implementierung des Index verantwortlich ist, basieren die im Folgenden besprochenen Indizes alle auf der InnoDB-Engine von MySQL.
Clustered Index
Clustering bedeutet, dass Datenzeilen und benachbarte Schlüsselwertcluster zusammen gespeichert werden. Bei einigen Datenbanken können Sie einen bestimmten Index als Clustered-Index auswählen, während in der Implementierung von InnoDB der Primärschlüsselindex direkt als Clustered-Index bezeichnet wird. Wenn kein Primärschlüssel definiert ist, wählt InnoDB einen eindeutigen Index ungleich Null, um den Primärschlüsselindex zu ersetzen. Wenn ein solcher Index nicht definiert ist, definiert InnoDB implizit einen Primärschlüssel als Clustered-Index (row_id).
Ein Beispiel für einen Clustered-Index ist wie in der Abbildung dargestellt:
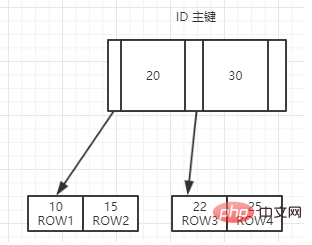
Nicht-Clustered-Index-Index
Ausschließen des Primärschlüssels in InnoDB Mit Ausnahme des Index ist alles andere ein nicht gruppierter Index, daher wird er auch als Nicht-Primärschlüsselindex bezeichnet. Die Blattknoten von Nicht-Primärschlüsselindizes speichern nicht den Wert einer Zeile, sondern den Primärschlüsselwert einer bestimmten Zeile. Die Definition von Clustering ist nicht erfüllt.
Ein Beispiel für einen nicht gruppierten Index ist wie in der Abbildung dargestellt:
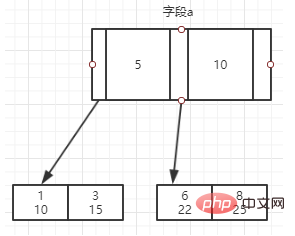
Der Unterschied zwischen gruppiertem Index und nicht gruppiertem Index in Abfrage
Wie aus den beiden Indexbeispieldiagrammen oben ersichtlich ist, werden die Datenzeilen direkt abgefragt und zurückgegeben, wenn die Abfrage über den Primärschlüsselindex erfolgt. Wenn Sie jedoch einen Nicht-Primärschlüsselindex abfragen, müssen Sie zunächst den Primärschlüssel über den Index ermitteln und dann den erhaltenen Primärschlüssel verwenden, um die Daten der spezifischen Zeile aus dem Primärschlüsselindex zu finden Das Abrufen von Daten aus dem Primärschlüsselindex über den erhaltenen Primärschlüssel wird als Rückkehr zur Tabelle bezeichnet.
Der Prozess der Rückgabe der Tabelle macht die Abfrage über einen gewöhnlichen Index einen Schritt länger als die Abfrage über den Primärschlüsselindex, und in vielen Fällen ist die Effizienz relativ gering. Wenn wir in unserem Abfrageprozess die Daten nur über den Primärschlüssel ermitteln können, ist es daher am besten, die Abfrage direkt über den Primärschlüssel durchzuführen.
Abdeckender Index
Oben wird der Prozess der Rückgabe der Tabelle durch Nicht-Primärschlüssel-Abfragen beschrieben. Es ist jedoch zu beachten, dass nicht jede Abfrage den Rückgabeprozess umfasst Erstens speichern die Blattknoten eines gewöhnlichen Index den Wert des Primärschlüssels. Was ist, wenn die Daten, die ich jetzt benötige, nur der Wert des Primärschlüssels sind? Nachdem der Wert des Primärschlüssels über den normalen Index abgerufen wurde, ist es nicht erforderlich, ihn im Primärschlüsselindex nachzuschlagen, sodass kein Prozess zur Rückkehr zur Tabelle erforderlich ist.
Im obigen Beispiel enthält der Nicht-Primärschlüsselindex bereits den von uns benötigten Wert, daher wird dieser Index auch als Abdeckindex bezeichnet. Der Covering-Index ist keine feste Struktur. Er kann ein einzelner Index (ein Index für ein Feld) oder ein zusammengesetzter Index sein. Alles, was Abfrageergebnisse direkt liefern kann, ohne dass ein Tabellenrückgabeprozess durchgeführt werden muss, kann als Covering-Index bezeichnet werden.
Oft ist es für uns unmöglich, Daten nur über den Primärschlüssel zu ermitteln. Die Verwendung gewöhnlicher Indizes kann zu Ineffizienz führen, daher sind Abdeckindizes auch eine sehr häufige Methode zur Leistungsoptimierung im täglichen Entwicklungsprozess.
Natürlich ist es nicht immer gut, Indexseiten abzudecken. Ich habe jetzt beispielsweise einen Index index(a,b) erstellt. Der Vorteil der Erstellung eines Index mit zwei Feldern, a und b, besteht darin, dass die Tabelle bei der Abfrage des ab-Felds nicht zurückgegeben wird. Wenn Sie jedoch nur über das b-Feld abfragen, können Sie diesen Index nicht verwenden. Die Indexelemente des erstellten Index werden entsprechend der Reihenfolge der Felder sortiert, die in der Indexdefinition erscheinen.
Prinzip des Präfixes ganz links
Angenommen, es gibt einen Indexindex (a, b). Wenn Sie dann über a und b abfragen, kann der Index angewendet und verwendet werden a allein auf Die Abfrage kann auch auf den Index angewendet werden. Wenn Sie jedoch b allein zum Abfragen verwenden, kann sie nicht auf den Index angewendet werden. Dies ist das Prinzip des Präfixes ganz links. Beim Abgleichen des Indexes werden die ganz linken Felder des Indexes abgeglichen. Wenn sie übereinstimmen können, kann der Index angewendet werden.
Aufgrund der Existenz des Präfixprinzips ganz links müssen wir beim Erstellen eines Index möglicherweise weitere Dinge berücksichtigen.
Zunächst muss man sich darüber im Klaren sein, dass es sich bei einem Index um eine Datenstruktur handelt. Je mehr Indizes erstellt werden, desto besser Indizes sollten je nach Bedarf so weit wie möglich reduziert werden.
Das Vorhandensein des Präfixprinzips ganz links ermöglicht die Verwendung eines gemeinsamen Index als Mehrfachindex. Voraussetzung ist natürlich, dass die Reihenfolge der Felder im Index festgelegt ist (tatsächlich gilt das Präfixprinzip ganz links). Gilt nicht nur für den Union-Index, sondern wird auch für den String-Index verwendet. Die n Zeichen ganz links im String-Index entsprechen den n Feldern ganz links im Union-Index.
Zum Beispiel index(a,b), mit diesem Index müssen wir keinen separaten Index für a erstellen, daher stellen wir beim Entwerfen eines gemeinsamen Index im Allgemeinen die Felder mit der höheren Nutzungshäufigkeit an die erste Stelle .
Verschieben Sie dann die Felder mit höherer Diskriminierung nach vorne. Die Diskriminierung ist die Wiederholungsrate der Werte im Feld. Je niedriger die Wiederholungsrate, desto höher ist die Diskriminierung. Beispielsweise ist das Geschlecht nicht als Index geeignet. Felder mit höherer Unterscheidung können nach einem Filter mehr Zeilen herausfiltern.
Dann ist die Größe des Feldes zu berücksichtigen. Da der Index auch Platz beanspruchen muss, werden im Allgemeinen kleinere Felder ausgewählt.
Referenzmaterialien
Interne Referenz für MySQL-Betrieb und -Wartung: MySQL, Galera, Inception-Kernprinzipien und Best Practices
Das obige ist der detaillierte Inhalt vonVerstehen Sie die Indizes in MySQL in einem Artikel. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

