Die Bedeutung des räumlichen Index

Räumlicher Index bezieht sich auf eine Datenstruktur, die in einer bestimmten Reihenfolge basierend auf der Position und Form von räumlichen Objekten oder einer bestimmten räumlichen Beziehung zwischen räumlichen Objekten angeordnet ist. Er enthält zusammenfassende Informationen zu räumlichen Objekten, wie z. B. Objektidentifikation und umschriebene Rechtecke Zeiger auf räumliche Objektentitäten.

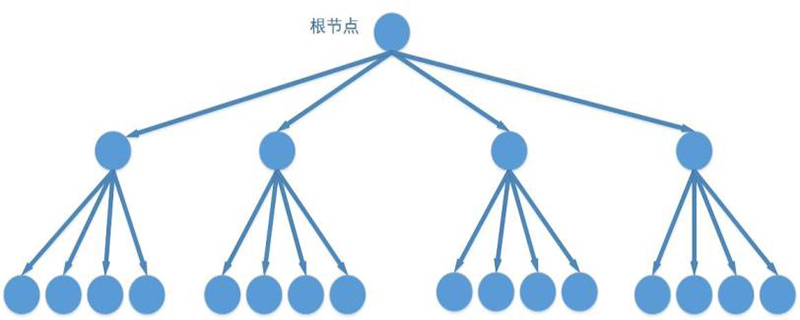
Die räumliche Datenabfrage ist ein räumlicher Index, der eine Beschreibung der auf dem Medium gespeicherten Datenstandortinformationen darstellt. Er wird verwendet, um die Effizienz der Datenerfassung zu verbessern Wird vom System als räumliche Zugriffsmethode (Spatial Access Method SAM) bezeichnet. Es bezieht sich auf eine Datenstruktur, die in einer bestimmten Reihenfolge basierend auf der Position und Form von räumlichen Objekten oder einer bestimmten räumlichen Beziehung zwischen räumlichen Objekten angeordnet ist. Sie enthält zusammenfassende Informationen zu räumlichen Objekten, wie z. B. das umschriebene Rechteck der Objektidentifikation und Zeiger auf die räumlichen Objektentitäten . (Empfohlenes Lernen: PHP-Video-Tutorial)

Bedeutung

Als zusätzliche räumliche Datenstruktur liegt der räumliche Index zwischen den Räumen Der Operationsalgorithmus und das räumliche Objekt filtern eine große Anzahl räumlicher Objekte heraus, die für die spezifische räumliche Operation irrelevant sind, wodurch die Geschwindigkeit und Effizienz der räumlichen Operation verbessert wird.

Zu den gängigen räumlichen Indextypen gehören BSP-Bäume, K-D-B-Bäume, R-Bäume, R+-Bäume und CELL-Bäume. Die überlegene Leistung räumlicher Indizes wirkt sich direkt auf räumliche Datenbanken und geografische Informationssysteme aus. Räumliche Indizes vom Rastertyp mit relativ einfachen Strukturen werden häufig in verschiedenen GIS-Software und -Systemen (z. B. ArcGIS) verwendet.

Die Fraktaltheorie ist ein neuer Zweig der modernen Mathematik. Fraktale Geometrie ist eine Geometrie, deren Forschungsgegenstand unregelmäßige geometrische Formen ist. Durch eingehende Forschung zur Fraktaltheorie wurden einige Eigenschaften von Peano-Kurven bewiesen, insbesondere die Hilbert-Raumfüllung, die das notwendige theoretische Wissen für die Untersuchung räumlicher Indizes liefert.

Geodaten sind einer der zentralen Forschungsinhalte im Bereich der Geoinformationen. Mit der rasanten Entwicklung des Aufbaus von Geoinformationsinfrastrukturen und der Geodatenerfassungstechnologie wird der Umfang der Geodaten immer größer Die Anforderungen an die gemeinsame Nutzung von Geodaten steigen. Gleichzeitig stellen Geodatenlager, Geodaten-Mining und andere Systemleistungen wachsende Anforderungen. Da es immer schwieriger wird, sich auf Hardware zu verlassen, um die Leistung von Datenbanksystemen zu verbessern, sind die Verbesserung der Möglichkeiten zur gemeinsamen Nutzung von Geodaten und die Verbesserung der Indexierungseffizienz von Geodaten zu einem wichtigen Forschungsgebiet geworden.

Basierend auf der Fraktaltheorie werden räumliche Daten durch die Generierung von Hilbert-Kurven effektiv und sinnvoll aufgeteilt und mit dem weit verbreiteten R-Baum-Raum im aktuellen räumlichen Indexsystem kombiniert, um einen neuen räumlichen Indexalgorithmus und ein neues räumliches Indexsystem zu bilden Löst die Probleme der räumlichen Indexgeschwindigkeit und Indexgenauigkeit gut und verbessert die räumliche Indexeffizienz verteilter massiver räumlicher Daten. Die Einzelheiten lauten wie folgt: Es wurden eine eingehende Untersuchung der Codierungstheorie fraktaler Grafiken, die Methode zum Zeichnen fraktaler Grafiken durch das L-System und das iterative Funktionssystem, ein Generierungsschema für Hilbert-Raumfüllungskurven und ein Scan-Matrix-Algorithmus entworfen.

Weitere technische Artikel zum Thema PHP finden Sie in der Spalte PHP-Grafik-Tutorial, um mehr darüber zu erfahren!

Das obige ist der detaillierte Inhalt vonDie Bedeutung des räumlichen Index. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!