Heim >Web-Frontend >CSS-Tutorial >So führen Sie mit CSS eine reguläre Polygontransformation eines einzelnen Div durch
So führen Sie mit CSS eine reguläre Polygontransformation eines einzelnen Div durch
- little bottlenach vorne
- 2019-04-29 10:13:443157Durchsuche
Dieser Artikel verwendet ausschließlich CSS, um ein „einzelnes“ Div von einem regulären Dreieck in ein reguläres Achteck umzuwandeln (ein einzelnes Div kann höchstens ein reguläres Achteck sein) und nutzt schließlich den Animationseffekt, um es in ein reguläres Achteck umzuwandeln Polygon-Animation, und da regelmäßige Polygone viele trigonometrische Funktionsberechnungen erfordern, werden die Seiten regelmäßiger Polygone der Einfachheit halber auf 100 Pixel eingestellt.
Sechseckiges Dreieck
Ein gleichseitiges Dreieck muss keine Pseudoelemente verwenden. Es muss nur die Randbreite von p selbst festgelegt werden Wenn die Seitenlänge des gleichseitigen Dreiecks 100 Pixel beträgt, wird die Mittellinie auf 87 Pixel gerundet (100 x sin (60) = 87).
Also müssen wir die Länge und Breite von p auf 0 setzen, dann die Breite des unteren Randes auf 87px und Stellen Sie am linken und rechten Rand die Breite auf 50 Pixel (und die Farbe auf transparent) ein, um ein schönes Dreieck zu erhalten.
width:0; height:0; border-width:0 50px 87px ; border-style:solid; border-color:transparent transparent #095;
Quadrat
Quadrat sollte am einfachsten sein, stellen Sie einfach die Länge und Breite auf den gleichen Wert ein. Aber es gibt sie tatsächlich Zwei weitere Methoden bestehen darin, die Länge und Breite auf 0 und den oberen, unteren, linken und rechten Rand auf 50 Pixel festzulegen. Die zweite besteht darin, die Höhe auf 0 und die Breite auf 100 Pixel festzulegen Die Seitenbreite ist ebenfalls auf 100 eingestellt, was in Ordnung ist.
.a{
width:100px;
height:100px;
background:#c00;
}
.b{
width:0;
height:0;
border-width:50px;
border-style:solid;
border-color:#095;
}
.c{
width:100px;
height:0;
border-width:0 0 100px;
border-style:solid;
border-color:#069;
}Regelmäßiges Fünfeck
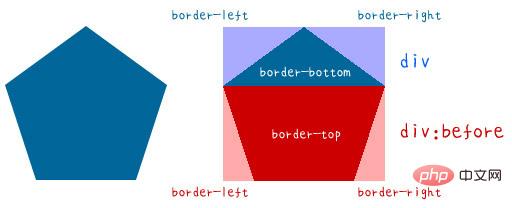
Das Regelmäßige Fünfeck muss in den Bereich der grundlegenden trigonometrischen Funktionen eintreten. Zerlegen wir zunächst das Regelmäßige Fünfeck. Verwenden Sie das ursprüngliche p als oberes Dreieck und erstellen Sie dann ein Pseudoelement, um das untere Trapez zu erstellen. Da der Winkel zwischen jeder Seite des regulären Fünfecks 108 Grad beträgt, können Sie das obere Dreieck mithilfe trigonometrischer Funktionen berechnen. 100 x cos(54)), die Breite beträgt 192px (100x sin(54) x 2), die Höhe des unteren Trapezes beträgt 95px (100 x sin(72)) und die Breite der langen Seite ist gleich Das Dreieck oben hat eine Größe von 192 Pixel.
Nachdem Sie das Prinzip verstanden haben, können Sie Pseudoelemente zum Zuordnen und Erstellen verwenden!
.a{
position:relative;
width:0;
height:0;
border-width:0 81px 59px;
border-style:solid;
border-color:transparent transparent #069;
}
.a:before{
position:absolute;
content:"";
top:59px;
left:-81px;
width:100px;
height:0;
background:none;
border-width:95px 31px 0;
border-style:solid;
border-color:#069 transparent transparent;
}
Regelmäßiges Sechseck
Jeder Winkel eines regelmäßigen Sechsecks beträgt 120 Grad, wenn man es in reiner CSS-Richtung betrachtet. Wenn ja, einfach Ändern Sie das Dreieck in ein regelmäßiges Fünfeck, um ein regelmäßiges Sechseck zu erhalten, das nur eine Kombination aus dem oberen und unteren Trapez ist. Die lange Seite des Trapezes beträgt 200 Pixel (100 x cos (60) x 2 + 100), die Höhe des Trapez ist 87px (100 x sin(60)).
Sie können also ein regelmäßiges Sechseck erstellen, indem Sie das CSS des regelmäßigen Fünfecks leicht modifizieren.
.a{
position:relative;
width:100px;
height:0;
border-width:0 50px 87px;
border-style:solid;
border-color:transparent transparent #f80;
}
.a:before{
position:absolute;
content:"";
top:87px;
left:-50px;
width:100px;
height:0;
background:none;
border-width:87px 50px 0;
border-style:solid;
border-color:#f80 transparent transparent;
}Regelmäßiges Siebeneck
Das After-Pseudoelement muss am Anfang des regelmäßigen Siebenecks verwendet werden, da es sich um das reguläre Siebeneck handelt Muss Es muss in drei Speicherblöcke zerlegt werden, wobei das ursprüngliche p als oberes Dreieck, ein Pseudoelement als mittleres Trapez und dann ein weiteres Pseudoelement als unteres Trapez verwendet werden. Die Winkel der regulären Siebenecke sind keine ganzen Zahlen 128 und 4/7 Grad, und die zweite Dezimalstelle beträgt ungefähr 128,57, sodass das berechnete Ergebnis wie in der folgenden Abbildung dargestellt ist. Der entscheidende Punkt ist, dass Sie die Länge und Breite genau kennen müssen.
Sobald Sie die Länge und Breite festgelegt haben, beginnen Sie mit dem Schreiben mit CSS!
.a{
position:relative;
width:0;
height:0;
border-width:0 90px 43px;
border-style:solid;
border-color:transparent transparent #09c;
}
.a:before{
position:absolute;
content:"";
top:140px;
left:-112px;
width:100px;
height:0;
border-width:78px 62px 0;
border-style:solid;
border-color:#09c transparent transparent;
}
.a:after{
position:absolute;
content:"";
top:43px;
left:-112px;
width:180px;
height:0;
border-width:0 22px 97px;
background:none;
border-style:solid;
border-color:transparent transparent #09c;
}Normales Achteck
Normales Achteck bedeutet eigentlich, das Dreieck auf dem regelmäßigen Siebeneck in ein Trapez zu verwandeln Das Trapez in der Mitte wird zu einem Rechteck. Der Winkel zwischen dem regulären Achteck beträgt 135 Grad. Die berechnete Länge und Breite jedes Bereichs ist wie folgt.
Mit dem gleichen Verständnis der Prinzipien ist CSS viel einfacher umzusetzen!
.a{
position:relative;
width:100px;
height:0;
border-width:0 71px 71px;
border-style:solid;
border-color:transparent transparent #f69;
}
.a:before{
position:absolute;
content:"";
top:171px;
left:-71px;
width:100px;
height:0;
border-width:71px 71px 0;
border-style:solid;
border-color: #f69 transparent transparent;
}
.a:after{
position:absolute;
content:"";
top:71px;
left:-71px;
width:242px;
height:0;
border-width:0 0 100px;
background:none;
border-style:solid;
border-color:transparent transparent #f69;
}小结
以上就是纯粹利用CSS做出来的单一div的正多边形变换,如果熟练的话,其实加上动画效果,就可以做出像下面示例这个样子的变换动画啰!

相关教程:css视频教程
Das obige ist der detaillierte Inhalt vonSo führen Sie mit CSS eine reguläre Polygontransformation eines einzelnen Div durch. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Empfohlene Video-Tutorials für den Einstieg in die CSS-Sprache
- Wie versteht man die Beziehung zwischen HTML, CSS und JavaScript?
- Eine Zusammenfassung häufig verwendeter CSS-Namenskonventionen, sehr praktisch (Sammlung)
- Verwenden Sie CSS, um ein Hover-Übergangsanimationsprojekt abzuschließen (super einfach)











